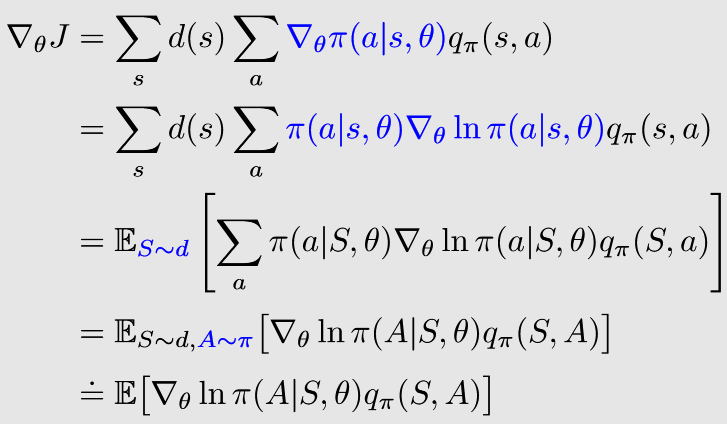强化学习的数学原理学习笔记 - 策略梯度（Policy Gradient）

---

本系列文章介绍强化学习基础知识与经典算法原理，大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程（参考资料1），并参考了部分参考资料2、3的内容进行补充。

系列博文索引：

• 强化学习的数学原理学习笔记 - RL基础知识
• 强化学习的数学原理学习笔记 - 基于模型（Model-based）
• 强化学习的数学原理学习笔记 - 蒙特卡洛方法（Monte Carlo）
• 强化学习的数学原理学习笔记 - 时序差分学习（Temporal Difference）
• 强化学习的数学原理学习笔记 - 值函数近似（Value Function Approximation）
• 强化学习的数学原理学习笔记 - 策略梯度（Policy Gradient）
• 强化学习的数学原理学习笔记 - Actor-Critic

参考资料：

1. 【强化学习的数学原理】课程：从零开始到透彻理解（完结）（主要）
2. Sutton & Barto Book: Reinforcement Learning: An Introduction
3. 机器学习笔记

*注：【】内文字为个人想法，不一定准确

概览：RL方法分类

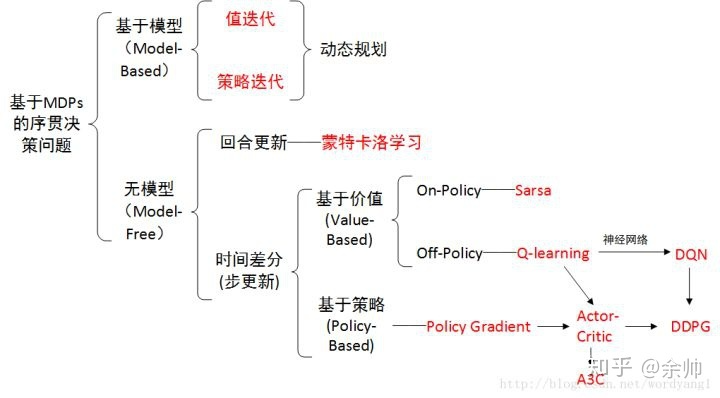
*图源：https://zhuanlan.zhihu.com/p/36494307

策略梯度（Policy Gradient）

在先前的内容中，策略用表（tabular）的形式进行表达，其也可以用函数的形式进行表达（尤其是当状态空间或动作空间连续或非常大时），优势在于降低存储开销和提升泛化能力。

之前的方法（值函数近似）称之为Value-based，而策略梯度（Policy Gradient）和Actor-Critic均为Policy-based。Value-based方法围绕状态值/动作值设计，而Policy-based优化关于策略的目标函数，从而直接得到最优策略。

Basic Policy Gradient

将策略表示为参数化函数：$\pi (a|s,\theta )$，其中$\theta \in {\mathbb{R}}^m$为参数向量，$\pi$是关于$\theta$的函数。
*其他写法：$\pi (a,s,\theta )$，${\pi }_{\theta }(a|s)$，${\pi }_{\theta }(a,s)$

与tabular representation的区别：

1. 最优策略：不是能够最大化每个状态值的策略，而是能够最大化特定scalar metrics的策略
2. 动作概率：不能直接获取，需要进行计算
3. 策略更新：不能直接更新，需要通过改变参数$\theta$来进行改变

策略梯度方法通过优化指定目标函数$J(\theta )$，直接得到最优策略：
$${\theta }_{t+1}={\theta }_t+\alpha {?}_{\theta }J({\theta }_t)$$
目标函数$J(\theta )$通常有以下两种类型：平均状态值${\bar{v}}_{\pi }$和平均单步奖励${\bar{r}}_{\pi }$。实际上，当奖励折扣值$\gamma <1$时，二者是等价的：${\bar{r}}_{\pi }=(1?\gamma ){\bar{v}}_{\pi }$。

目标函数1：平均状态值

平均状态值（average state value / average value）：
$${\bar{v}}_{\pi }=\sum _{s\in \mathcal{S}}d(s)v_{\pi }(s)=\mathbb{E}[v_{\pi }(S)]$$
其中，$d(s)\ge 0$且${\sum }_{s\in \mathcal{S}}d(s)=1$，因此$d(s)$既可以看作是状态$s$的权重，也可以看作是随机变量$S$的概率分布。

其他形式：${\bar{v}}_{\pi }=\mathbb{E}\left[{\sum }_{t=0}^{\infty }{\gamma }^t{R}_{t+1}\right]$

向量形式：${\bar{v}}_{\pi }=d^T{v}_{\pi }$

在常见的情况下，$d$是取决于$\pi$的平稳分布，即$d_{\pi }(s)$，其具有以下性质：
$d_{\pi }^T{P}_{\pi }=d_{\pi }^T$
其中，$P_{\pi }$是状态转移概率矩阵。

目标函数2：平均单步奖励

平均单步奖励（average one-step reward / average reward）
$${\bar{r}}_{\pi }=\sum _{s\in \mathcal{S}}d(s)r_{\pi }(s)=\mathbb{E}[r_{\pi }(S)]$$
其中，$S～d_{\pi }$，$d_{\pi }$为平稳分布。$r_{\pi }(s)={\sum }_{a\in \mathcal{A}}\pi (a|s)r(s,a)$为策略$\pi$在状态$s$下取得的平均单步奖励，而$r(s,a)=\mathbb{E}[R|s,a]={\sum }_{r}rp(r|s,a)$。

另一种形式：
假设agent遵循一个策略生成了奖励为$(R_{t+1},R_{t+2},?)$的trajectory，其平均单步奖励为：
${\lim }_{n\to \infty }\frac{1}{n}\mathbb{E}[{\sum }_{k=1}^n{R}_{t+k}|S_t=s_0]$
其中，$s_0$为该trajectory的起始状态。考虑无穷多步的极限，上式等价于【似乎是与平稳随机过程有关，时间平均等于统计平均，不确定】：
${\lim }_{n\to \infty }\frac{1}{n}\mathbb{E}\left[{\sum }_{k=1}^n{R}_{t+k}\right]={\bar{r}}_{\pi }$

🟡PG梯度计算

策略梯度方法的梯度计算可以统一总结为下式：
$${?}_{\theta }J(\theta )=\sum _{s\in \mathcal{S}}\eta (s)\sum _{a\in \mathcal{A}}{?}_{\theta }\pi (a|s,\theta )q_{\pi }(s,a)$$
其中：

• $J(\theta )$可以为${\bar{v}}_{\pi }$、${\bar{r}}_{\pi }$或${\bar{v}}_{\pi }^0$
• $=$可以为相等、约等$\approx$、成比例$\propto$
• $\eta$是状态的分布或权重（如上文中的$d_{\pi }$）

进一步地，可以基于下式计算梯度：
$${?}_{\theta }J(\theta )=\mathbb{E}[{?}_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)]$$
其中，$S～\eta$且$A～\pi (A|S,\theta )$。通过随机采样的方式估计期望，则有：
$${?}_{\theta }J(\theta )\approx {?}_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)$$

注意：为了计算对数$\ln$，对所有的$s,a,\theta$，策略必须满足：$\pi (a|s,\theta )>0$。即：策略必须是随机性（stochastic）的，且为探索性（exploratory）的。(*确定性策略见后续介绍Actor-Critic的博文中的DPG)
这可以通过softmax实现，将向量从$(?\infty ,+\infty )$限界至$(0,1)$。softmax限界后的形式为：
$\pi (a|s,\theta )=\frac{e^{h(s,a,\theta )}}{{\sum }_{a^{\prime }\in \mathcal{A}}{e}^{h(s,a^{\prime },\theta )}}$
其中，$h(s,a,\theta )$类似于特征函数，具体由神经网络确定。

推导：
已知$\frac{\mathrm{d}\ln x}{\mathrm{d}x}=\frac{1}{x}$，则$?\ln f(x)=\frac{?f(x)}{f(x)}$，故有：${?}_{\theta }\ln \pi (a|s,\theta )=\frac{{?}_{\theta }\pi (a|s,\theta )}{\pi (a|s,\theta )}$
进一步地，$\pi$的梯度可以计算为：${?}_{\theta }\pi (a|s,\theta )=\pi (a|s,\theta ){?}_{\theta }\ln \pi (a|s,\theta )$

🟦REINFORCE

策略梯度（PG）方法基于梯度上升方法最大化目标函数：
${\theta }_{t+1}={\theta }_t+\alpha \mathbb{E}[{?}_{\theta }\ln \pi (A|S,{\theta }_t)q_{\pi }(S,A)]$

实际中，通过随机采样的方式估计期望与$q_{\pi }(s_t,a_t)$，有：
$${\theta }_{t+1}={\theta }_t+\alpha {?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t)q_t(s_t,a_t)$$

注意：$A～\pi (A|S,\theta )$，$a_t$的采样依赖于状态$s_t$下的策略$\pi ({\theta }_t)$，因此策略梯度是on-policy方法。

估计$q_{\pi }(s_t,a_t)$有两种方法：

• 蒙特卡洛（MC）：REINFORCE（策略梯度的代表性算法）
• 时序差分（TD）：Actor-Critic系列算法（见后续博文）

REINFORCE算法步骤（伪代码）：
初始化：$\pi (a|s,\theta )$，$\gamma \in (0,1)$，$\alpha >0$
目标：最大化$J(\theta )$
步骤：在第$k$次迭代中，选择策略$\pi ({\theta }_k)$的起始状态$s_0$，设其episode为 { s 0 , a 0 , r 1 , ? ? , s T ? 1 , a T ? 1 ， r T } \{ s_0, a_0, r_1, \cdots, s_{T-1}, a_{T-1}， r_T \} {s0?,a0?,r1?,?,sT?1?,aT?1?，rT?}

• 在每个时间步$t=0,1,?,T?1$：
  • 值更新（蒙特卡洛方法）：$q_t(s_t,a_t)={\sum }_{k=t+1}^T{\gamma }^{k?t?1}{r}_k$
  • 策略更新：更新参数${\theta }_{t+1}$，公式见上
    • *注意：蒙特卡洛是offline的，需要整个episode的数据，所以这里更新完参数后不立即使用策略去采集数据
• ${\theta }_k={\theta }_T$，在下次迭代中生成下一组episode的数据