C#，字符串匹配（模式搜索）RK（Rabin Karp）算法的源代码

?M.O.Rabin

Rabin-Karp算法，是由M.O.Rabin和R.A.Karp设计实现的一种基于移动散列值的字符串匹配算法。

通常基于散列值的字符串匹配方法：（1）首先计算模式字符串的散列函数；（2）然后利用相同的散列函数计算文本中所有可能的M个字符的子字符串的散列函数值并寻找匹配。但是这种方法比暴力查找还慢，因为计算散列值会涉及字符串中的每个字符。Rabin和Karp对上述方法进行了改进，设计实现了一种能够在常数时间内算出M个字符的子字符串散列值的方法。

运行效果：

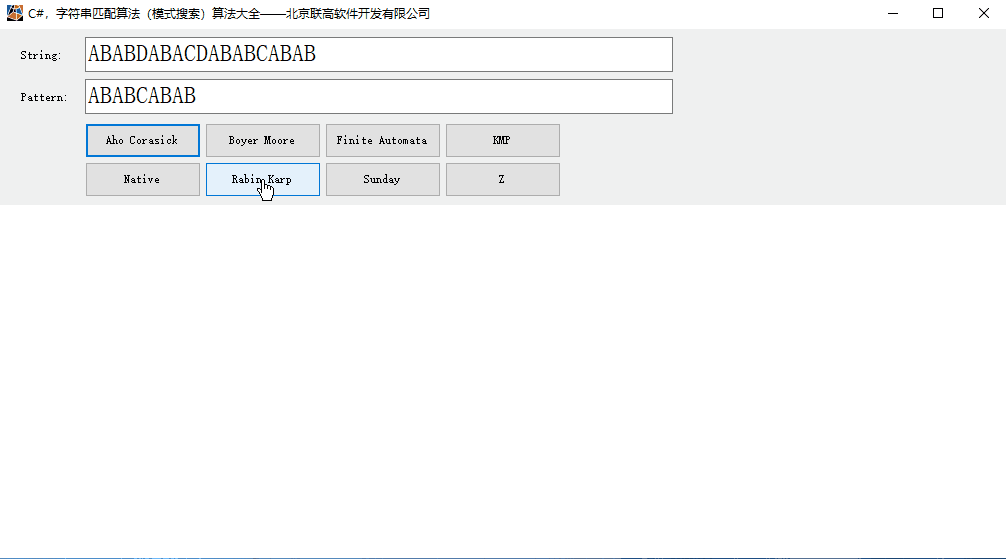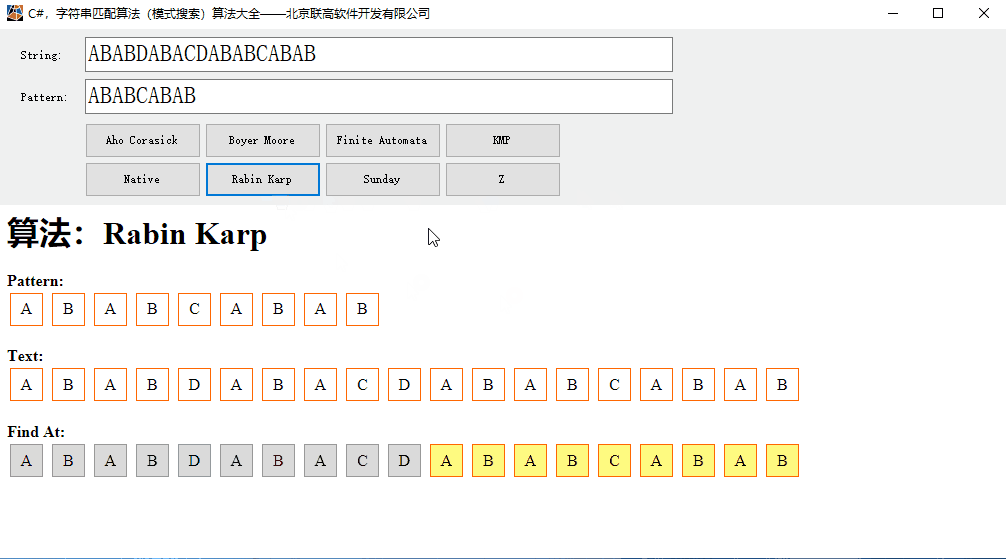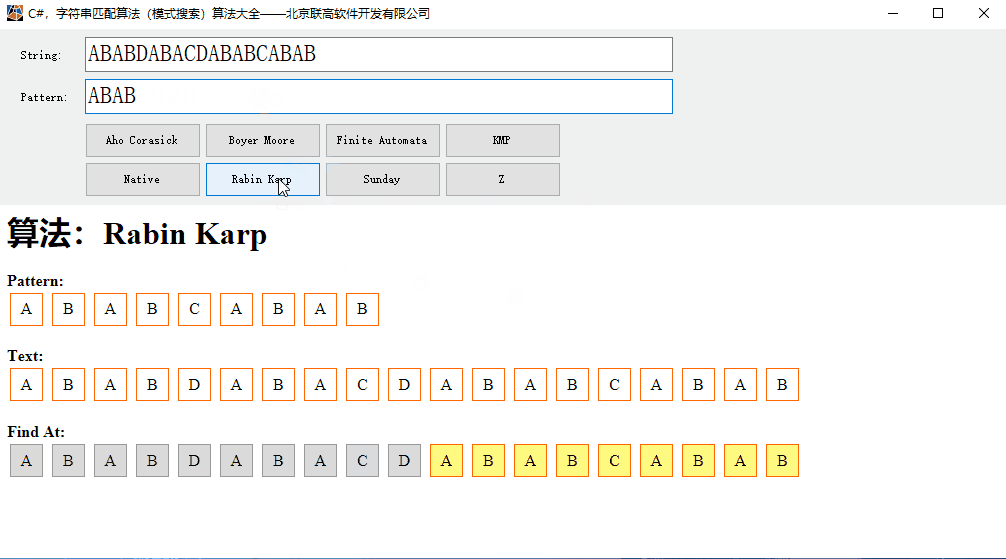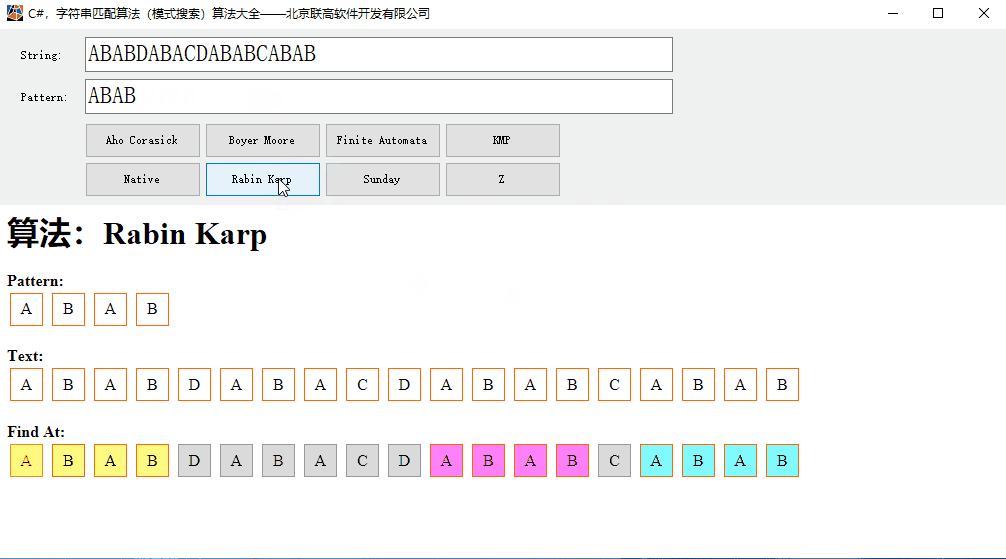
源代码：

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
?? ?public static partial class PatternSearch
?? ?{
?? ??? ?public readonly static int ALPHA_CODE_MAX = 256;

?? ??? ?/// <summary>
?? ??? ?/// 字符串匹配算法（模式搜索）Rabin Karp 算法
?? ??? ?/// </summary>
?? ??? ?/// <param name="text"></param>
?? ??? ?/// <param name="pattern"></param>
?? ??? ?/// <param name="primeNumber"></param>
?? ??? ?/// <returns></returns>
?? ??? ?public static List<int> Rabin_Karp_Search( string text,string pattern, int primeNumber = 101)
?? ??? ?{
?? ??? ??? ?List<int> matchs = new List<int>();

?? ??? ??? ?int M = pattern.Length;
?? ??? ??? ?int N = text.Length;

?? ??? ??? ?int h = 1;
?? ??? ??? ?for (int i = 0; i < M - 1; i++)
?? ??? ??? ?{
?? ??? ??? ??? ?h = (h * ALPHA_CODE_MAX) % primeNumber;
?? ??? ??? ?}

?? ??? ??? ?int p = 0;
?? ??? ??? ?int t = 0;
?? ??? ??? ?for (int i = 0; i < M; i++)
?? ??? ??? ?{
?? ??? ??? ??? ?p = (ALPHA_CODE_MAX * p + pattern[i]) % primeNumber;
?? ??? ??? ??? ?t = (ALPHA_CODE_MAX * t + text[i]) % primeNumber;
?? ??? ??? ?}

?? ??? ??? ?for (int i = 0; i <= N - M; i++)
?? ??? ??? ?{
?? ??? ??? ??? ?if (p == t)
?? ??? ??? ??? ?{
?? ??? ??? ??? ??? ?int j;
?? ??? ??? ??? ??? ?for (j = 0; j < M; j++)
?? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ?if (text[i + j] != pattern[j])
?? ??? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ??? ?break;
?? ??? ??? ??? ??? ??? ?}
?? ??? ??? ??? ??? ?}

?? ??? ??? ??? ??? ?if (j == M)
?? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ?matchs.Add(i);
?? ??? ??? ??? ??? ?}
?? ??? ??? ??? ?}

?? ??? ??? ??? ?if (i < (N - M))
?? ??? ??? ??? ?{
?? ??? ??? ??? ??? ?t = (ALPHA_CODE_MAX * (t - text[i] * h) + text[i + M]) % primeNumber;
?? ??? ??? ??? ??? ?if (t < 0)
?? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ?t = (t + primeNumber);
?? ??? ??? ??? ??? ?}
?? ??? ??? ??? ?}
?? ??? ??? ?}

?? ??? ??? ?return matchs;
?? ??? ?}
?? ?}
}
?

----------------------------------------------------------------

POWER BY TRUFFER.CN

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
?? ?public static partial class PatternSearch
?? ?{
?? ??? ?public readonly static int ALPHA_CODE_MAX = 256;

?? ??? ?/// <summary>
?? ??? ?/// 字符串匹配算法（模式搜索）Rabin Karp 算法
?? ??? ?/// </summary>
?? ??? ?/// <param name="text"></param>
?? ??? ?/// <param name="pattern"></param>
?? ??? ?/// <param name="primeNumber"></param>
?? ??? ?/// <returns></returns>
?? ??? ?public static List<int> Rabin_Karp_Search( string text,string pattern, int primeNumber = 101)
?? ??? ?{
?? ??? ??? ?List<int> matchs = new List<int>();

?? ??? ??? ?int M = pattern.Length;
?? ??? ??? ?int N = text.Length;

?? ??? ??? ?int h = 1;
?? ??? ??? ?for (int i = 0; i < M - 1; i++)
?? ??? ??? ?{
?? ??? ??? ??? ?h = (h * ALPHA_CODE_MAX) % primeNumber;
?? ??? ??? ?}

?? ??? ??? ?int p = 0;
?? ??? ??? ?int t = 0;
?? ??? ??? ?for (int i = 0; i < M; i++)
?? ??? ??? ?{
?? ??? ??? ??? ?p = (ALPHA_CODE_MAX * p + pattern[i]) % primeNumber;
?? ??? ??? ??? ?t = (ALPHA_CODE_MAX * t + text[i]) % primeNumber;
?? ??? ??? ?}

?? ??? ??? ?for (int i = 0; i <= N - M; i++)
?? ??? ??? ?{
?? ??? ??? ??? ?if (p == t)
?? ??? ??? ??? ?{
?? ??? ??? ??? ??? ?int j;
?? ??? ??? ??? ??? ?for (j = 0; j < M; j++)
?? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ?if (text[i + j] != pattern[j])
?? ??? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ??? ?break;
?? ??? ??? ??? ??? ??? ?}
?? ??? ??? ??? ??? ?}

?? ??? ??? ??? ??? ?if (j == M)
?? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ?matchs.Add(i);
?? ??? ??? ??? ??? ?}
?? ??? ??? ??? ?}

?? ??? ??? ??? ?if (i < (N - M))
?? ??? ??? ??? ?{
?? ??? ??? ??? ??? ?t = (ALPHA_CODE_MAX * (t - text[i] * h) + text[i + M]) % primeNumber;
?? ??? ??? ??? ??? ?if (t < 0)
?? ??? ??? ??? ??? ?{
?? ??? ??? ??? ??? ??? ?t = (t + primeNumber);
?? ??? ??? ??? ??? ?}
?? ??? ??? ??? ?}
?? ??? ??? ?}

?? ??? ??? ?return matchs;
?? ??? ?}
?? ?}
}