算法通关村番外篇-跳表

大家好我是苏麟 , 今天来聊聊调表 .

跳表很少很少实现所以我们只了解就可以了 .?

跳表

链表在查找元素的时候，因为需要逐一查找，所以查询效率非常低，时间复杂度是O(N)，于是就出现了跳表。跳表是在链表基础上改进过来的，实现了一种「多层」的有序链表，这样的好处是能快读定位数据。

那跳表长什么样呢？我这里举个例子，下图展示了一个层级为 3 的跳表。

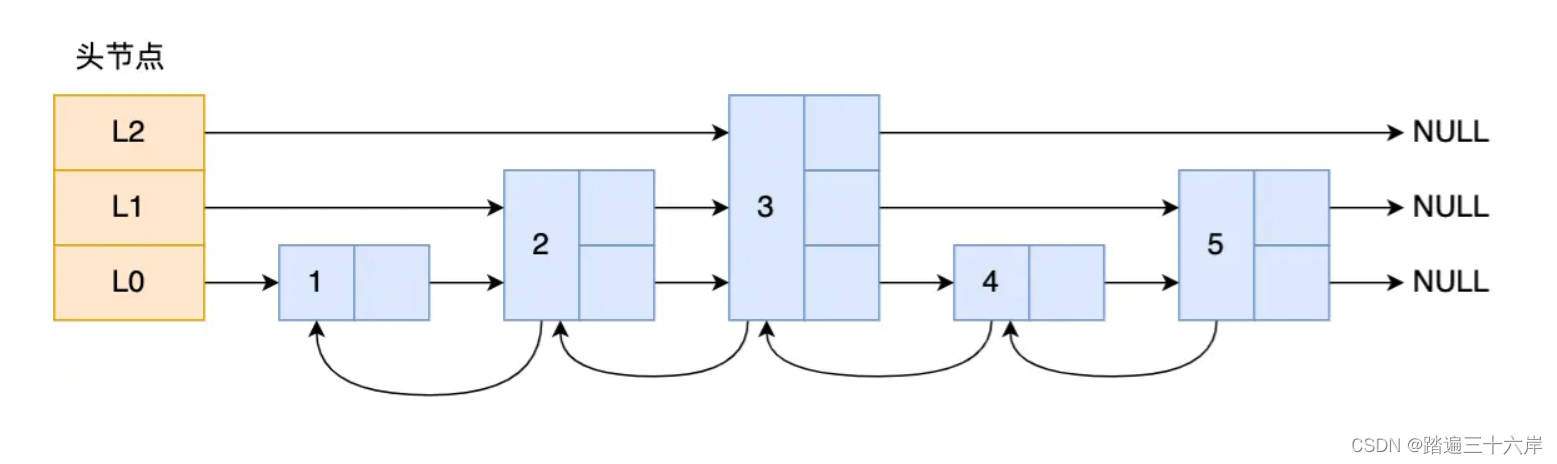
图中头节点有 L0~L2 三个头指针，分别指向了不同层级的节点，然后每个层级的节点都通过指针连接起来：

• L0 层级共有 5 个节点，分别是节点1、2、3、4、5；
• L1 层级共有 3 个节点，分别是节点 2、3、5；
• L2 层级只有 1 个节点，也就是节点 3 。

如果我们要在链表中查找节点 4 这个元素，只能从头开始遍历链表，需要查找 4 次，而使用了跳表后，只需要查找 2 次就能定位到节点 4，因为可以在头节点直接从 L2 层级跳到节点 3，然后再往前遍历找到节点 4。

可以看到，这个查找过程就是在多个层级上跳来跳去，最后定位到元素。当数据量很大时，跳表的查找复杂度就是 O(logN)。

跳表节点层数设置

跳表的相邻两层的节点数量的比例会影响跳表的查询性能。

举个例子，下图的跳表，第二层的节点数量只有 1 个，而第一层的节点数量有 6 个。

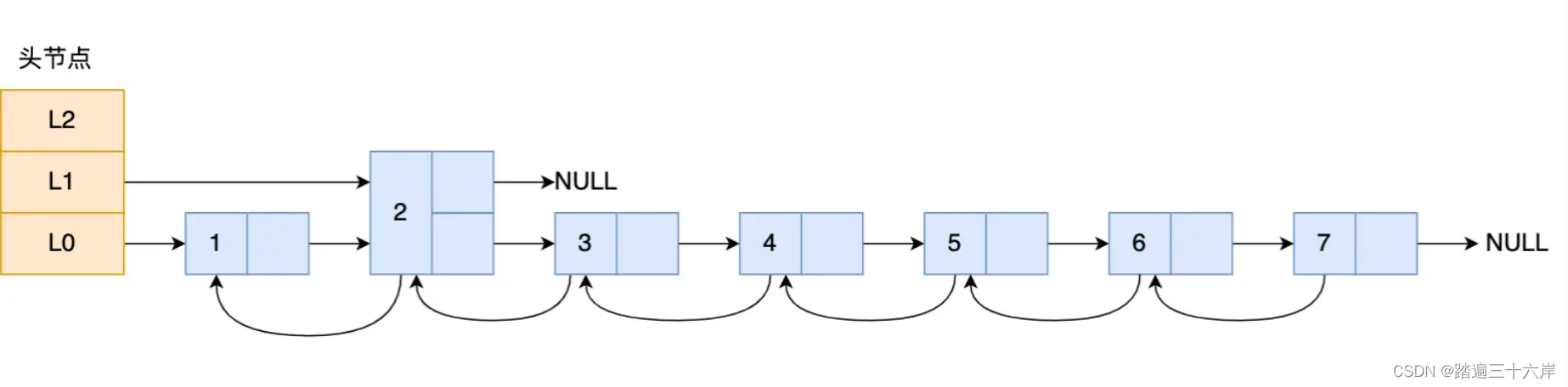
这时，如果想要查询节点 6，那基本就跟链表的查询复杂度一样，就需要在第一层的节点中依次顺序查找，复杂度就是 O(N) 了。所以，为了降低查询复杂度，我们就需要维持相邻层结点数间的关系。

跳表的相邻两层的节点数量最理想的比例是 2:1，查找复杂度可以降低到 O(logN)。

下图的跳表就是，相邻两层的节点数量的比例是 2 : 1。

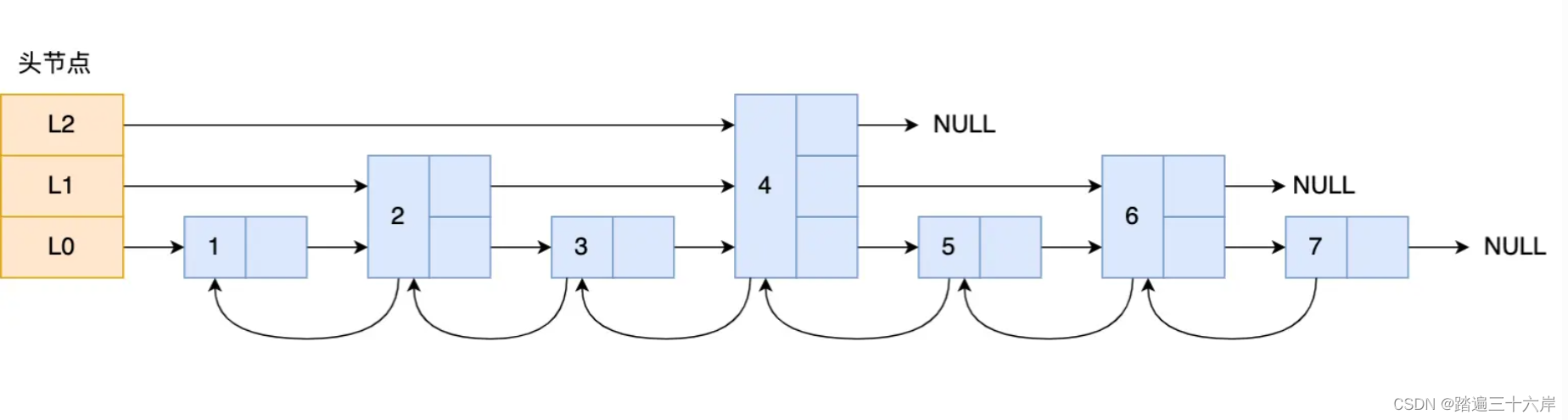
那怎样才能维持相邻两层的节点数量的比例为 2 : 1 呢？

如果采用新增节点或者删除节点时，来调整跳表节点以维持比例的方法的话，会带来额外的开销。

Redis 则采用一种巧妙的方法是，跳表在创建节点的时候，随机生成每个节点的层数，并没有严格维持相邻两层的节点数量比例为 2 : 1 的情况。

具体的做法是，跳表在创建节点时候，会生成范围为[0-1]的一个随机数，如果这个随机数小于 0.25（相当于概率 25%），那么层数就增加 1 层，然后继续生成下一个随机数，直到随机数的结果大于 0.25 结束，最终确定该节点的层数。

这样的做法，相当于每增加一层的概率不超过 25%，层数越高，概率越低，层高最大限制是 64。

虽然我前面讲解跳表的时候，图中的跳表的「头节点」都是 3 层高，但是其实如果层高最大限制是 64，那么在创建跳表「头节点」的时候，就会直接创建 64 层高的头节点。

跳表的插入与删除

假设我们要插入的节点是10，首先找到待插节点的前置节点（仅小于待插入节点）：

接下来，按照一般链表的插入方式，把节点10插到节点9的下一个 位置：

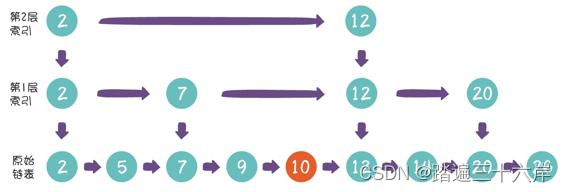
这样是不是插入工作就完成了呢？并不是。随着原始链表的新节 点越来越多，索引会渐渐变得不够用了，因此索引节点也需要相应做 出调整

如何调整索引呢？我们让新插入的节点随机“晋升”，也就是成 为索引节点。新节点晋升成功的几率是50%。

假设第一次随机的结果是晋升成功，那么我们把节点10作为索引 节点，插到第1层索引的对应位置，并且向下指向原始链表的节点10：

新节点在成功晋升之后，仍然有机会继续向上一层索引晋升。我 们再进行一次随机，假设随机的结果是晋升失败，那么插入操作就告 一段落了。

新节点10已经晋升到 第2层索引，下一次随机的结果仍然是晋升成功，这时候我们该怎么 办？

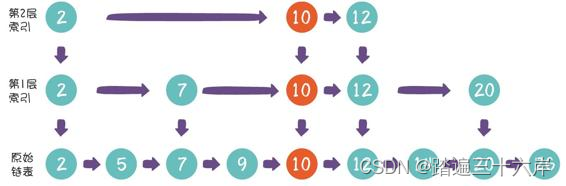
这时候，我们直接让索引增加一层，就像下面这样：

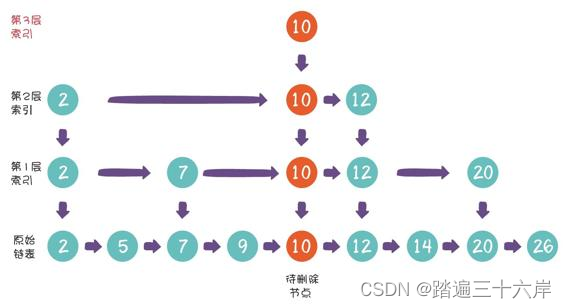
至于跳表删除节点的过程，则是相反的思路。

假设我们要从跳表中删除节点10，首先按照跳表查找节点的方 法，找到待删除的节点：

接下来，按照一般链表的删除方式，把节点10从原始链表当中删 除：

这样是不是删除工作就完成了呢？并不是。我们需要顺藤摸瓜， 把索引当中的对应节点也一一删除：

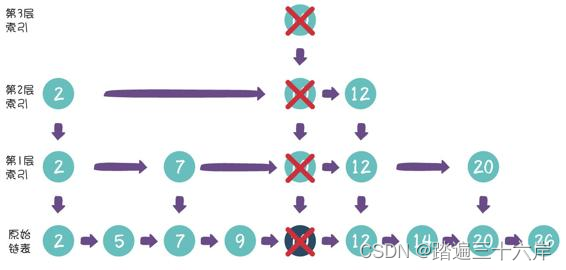
那么，如果某一层索引的节点被删光了，该怎么办呢？

很好解决，直接把没有节点的那一层删去就好了。

在刚才的例子当中，第3层索引的节点已经没有了，因此我们把整 个第3层删去：

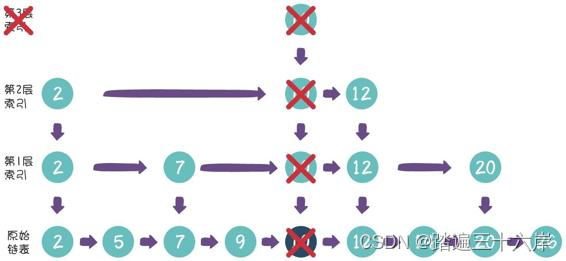
最终的删除结果如下：

---

这期就到这里 , 下期见!