洛谷P1196 [NOI2002] 银河英雄传说
P1196 [NOI2002] 银河英雄传说
题目背景
公元?5801年,地球居民迁至金牛座?α?第二行星,在那里发表银河联邦创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。
宇宙历?799年,银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征,气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。
题目描述
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在这次决战中,他将巴米利恩星域战场划分成?30000列,每列依次编号为?1,2,…,30000。之后,他把自己的战舰也依次编号为?1,2,…,30000,让第?i?号战舰处于第?i?列,形成“一字长蛇阵”,诱敌深入。这是初始阵形。当进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,实施密集攻击。合并指令为?M i j,含义为第?i?号战舰所在的整个战舰队列,作为一个整体(头在前尾在后)接至第?j?号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。
然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利的第?i?号战舰与第?j?号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以及回答莱因哈特的询问。
输入格式
第一行有一个整数?T(1≤T≤5×105),表示总共有T?条指令。
以下有T?行,每行有一条指令。指令有两种格式:
-
M i j:i?和?j?是两个整数(1≤i,j≤30000),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第?i?号战舰与第?j?号战舰不在同一列。 -
C i j:i?和?j?是两个整数(1≤i,j≤30000),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式
依次对输入的每一条指令进行分析和处理:
-
如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息。
-
如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,表示在同一列上,第?i?号战舰与第?j?号战舰之间布置的战舰数目。如果第i?号战舰与第?j?号战舰当前不在同一列上,则输出??1。
输入输出样例
输入 #1
4
M 2 3
C 1 2
M 2 4
C 4 2
输出 #1
-1
1
说明/提示
样例解释
战舰位置图:表格中阿拉伯数字表示战舰编号。
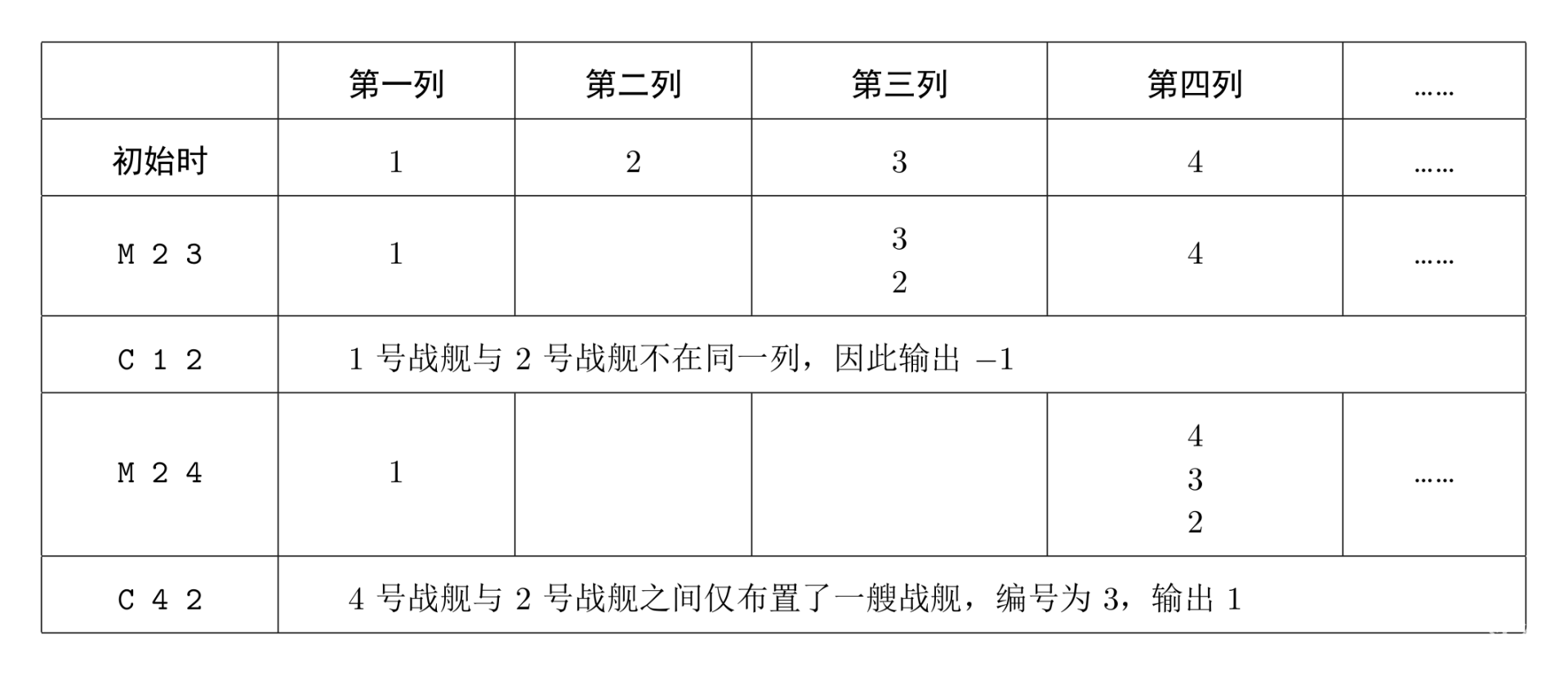
解题思路?
【题目大意】
有30000条队列,总共n次操作,分M操作与C操作,M操作是把当前第i艘飞船所在的整条队列移到第j艘飞船艘所在的队列的最后面,C操作则是询问第i艘飞船与第j艘飞船是否在同一条队列,如果在则输出第i艘飞船与第j艘飞船之间的飞船数,不包括i和j,题目不保证j在i后面,否则就输出-1。
初见这道题,首先想到的方法当然是直接模拟,模拟每一次指令。当然这种方法对于小数据行得通,但对于此题的500,000个指令,肯定超时。
因此我们就要想其它方法。
先来分析一下这些指令的特点,很容易发现对于每个M指令,只可能一次移动整个队列,并且是把两个队列首尾相接合并成一个队列,不会出现把一个队列分开的情况,因此,我们必须要找到一个可以一次操作合并两个队列的方法。
再来看下C指令:判断飞船i和飞船j是否在同一列,若在,则输出它们中间隔了多少艘飞船。我们先只看判断是否在同一列,由于每列一开始都只有一艘飞船,之后开始合并,结合刚刚分析过的M指令,很容易就想到要用并查集来实现。
定义一个数组fa,fa[i]表示飞船i的祖先节点,即其所在列的队头。再定义一个用于查找飞船祖先的函数find,在每次递归找祖先的同时更新fa,压缩路径,大大减小以后的时间消耗。初始时对于每个fa[i]都赋值为i,合并时就先分别查找飞船i和飞船j的祖先,然后将飞船i的祖先的祖先(即fa[飞船i的祖先])赋值为飞船j的祖先。最后每次判断时只需要找到飞船i和飞船j的祖先,判断是否是同一艘飞船,若是,则在同一列,反之,则不在。
现在,判断是否在同一列以及如何一次操作合并两个队列的问题已经解决,但还有问题需要解决:如何在以上方法的基础上,进一步得到两艘飞船之间的飞船。
AC:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 30010;
int father[maxn], height[maxn], size[maxn];
void init() {
for (int i = 1; i < maxn; ++i) {
father[i] = i;
height[i] = 0;
size[i] = 1;
}
}
int find(int x) {
if (father[x] == x) return x;
int t = father[x];
father[x] = find(t);
height[x] += height[t];
return father[x];
}
void merge(int a, int b) {
int x = find(a), y = find(b);
if (x == y) return;
father[x] = y;
height[x] += size[y];
size[y] += size[x];
}
bool query(int a, int b) { return find(a) == find(b); }
int main() {
int t, a, b;
char c[2];
scanf("%d", &t);
init();
while (t--) {
scanf("%s%d%d", c, &a, &b);
if (c[0] == 'M') merge(a, b);
else if (c[0] == 'C') {
if (!query(a, b)) printf("-1\n");
else printf("%d\n", abs(height[a] - height[b]) - 1);
}
}
return 0;
}
结尾
如果有人想在洛谷上做题,可以点下方链接:
如果你喜欢或想了解一下其他的算法,可以看看以下这些:
C++小游戏:
DFS深搜;
最后认识一下,我是爱编程的喷火龙廖,我们有缘再见!
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- [排序篇] 快速排序
- nodejs微信小程序+python+PHP在线学习与推荐系统设计与实现-计算机毕业设计推荐
- 桥接虚拟机设置上网步骤
- 【BUG】‘webpack-dev-server‘ 不是内部或外部命令,也不是可运行的程序或批处理文件。
- O&O DiskRecovery 14 - 专业硬盘SSD数据恢复工具软件
- Miniconda 3 | 出发,探索Python
- 【无标题】
- AI技术已经发现了一种新材料,可以在电池制造中减少对锂的需求
- 【ArcGIS Pro微课1000例】0032:创建具有指定高程Z值的矢量数据
- 达梦数据库 忘记 SYSDBA 密码 处理方法