机器学习实验报告——CART算法

基于以上假设，CART算法通过选择最优的属性进行划分，使得每个划分后的子集尽可能纯净。在分类问题中，每个子集中的样本点属于同一类别；在回归问题中，每个子集中的样本点具有相似的目标变量值。通过递归地划分数据集并构建决策树，CART算法能够在特征空间中创建一系列矩形区域，从而实现对新样本的分类或回归预测。

1.3 CART树的理解

CART(classification and regression tree)树：又称为分类回归树，从名字可以发现，CART树既可用于分类，也可以用于回归。

当数据集的因变量是离散值时，可以采用CART分类树进行拟合，用叶节点概率最大的类别作为该节点的预测类别。

当数据集的因变量是连续值时，可以采用CART回归树进行拟合，用叶节点的均值作为该节点预测值。

但需要注意的是，该算法是一个二叉树，即每一个非叶节点只能引伸出两个分支，所以当某个非叶节点是多水平(2个以上)的离散变量时，该变量就有可能被多次使用。

1.4 算法原理

决策树CART（Classification and Regression Trees）算法是一种基于二叉树结构的分类和回归算法，它通过选择最优属性进行数据划分，递归地构建决策树，并通过剪枝操作提高模型的泛化能力。

总的来说，CART算法原理可以分为两个部分：构建树和剪枝。

（1）构建树

首先，选择一个最优属性作为根节点，将数据集按照该属性的取值划分成子集。

对于每个子集，如果样本全属于同一类别（对于分类问题）或具有相似的目标变量值（对于回归问题），则将该节点标记为叶节点，并将其类别或目标变量值设置为节点的预测值。

否则，根据选择的属性再次划分子集，创建新的非叶节点，并递归地构建树。

在构建树的过程中，使用了不同的评测指标来选择最优属性作为划分点。

对于分类问题，通常使用基尼指数（Gini Index）或信息增益（Information Gain）来评估属性的纯度提升程度；

对于回归问题，通常使用平方误差最小化来评估属性的拟合程度。

分类树与回归树的一个区别是：如果目标变量是离散型变量则用分类树，如果目标变量是连续型变量则用回归树。

（2）剪枝：

为了避免过拟合（Overfitting），决策树在构建完成后需要进行剪枝操作。决策树剪枝的目标是通过减少决策树的复杂度，提高模型的泛化能力。

剪枝过程通常分为预剪枝（Pre-Pruning）和后剪枝（Post-Pruning）两种方法：

二、算法关键点

2.1分裂准则的选择

CART算法通过选择最优的分裂准则来进行数据划分，常用的准则包括基尼指数、信息增益、信息增益比和均方误差等。不同的分裂准则会导致不同的决策树结构和分类/回归性能，因此选择合适的分裂准则非常重要。

（1）对于分类问题，采用基尼指数作为分裂准则，以下对基尼指数进行介绍：

基尼指数(Gini index)

????????

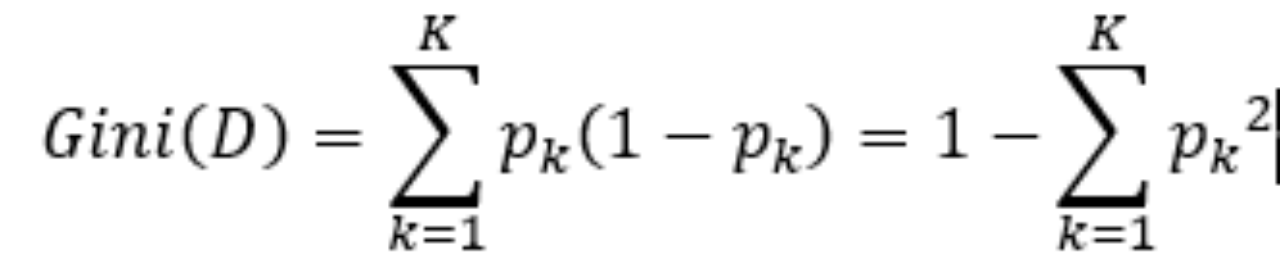从上面的公式可以发现，当数据集D中只有1个类时，pk=1，Gini(D)=0，说明基尼指数越小，样本纯度越高。

对于特征A，将集合D划分成D1和D2，基尼指数Gini(D,A)表示经过A=a划分后集合D的不确定性，公式如下：

???????

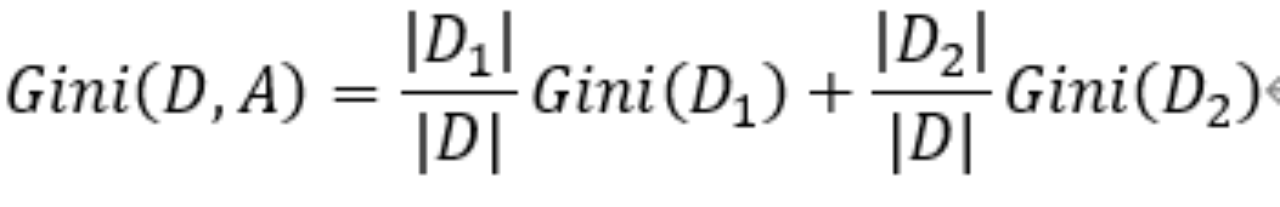其中|D|、|D1|、|D2|分别表示数据集D、D1、D2中样本数量。

（2）对于回归问题，采用残差平方和作为分裂准则

若yi表示训练集D={(x1,y1),(x2,y2),...,(xn,yn)}的输出变量，是连续值。f(xi)是预测值，则预测误差可以表示为：

????????????????

我们拟合的目标就是寻找最佳划分特征里的最佳划分点，找到每一个f(xi)，使得误差平方和最小化。

把误差平方和应用到CART回归树中，数学表达式如下：

?????

其中j、s分别表示第j个变量的划分点s，R1(j,s)表示在该划分下的左区域，R2(j,s)表示在该划分下的右区域，C1、C2为区域R1(j,s)、R2(j,s)的最优输出值(因变量均值)。

2.2 剪枝操作的实现

为了避免过拟合，CART算法通常需要对建立好的决策树进行剪枝操作。剪枝操作旨在降低决策树的复杂度，并提高其泛化性能。CART算法中的剪枝操作主要有预剪枝和后剪枝两种方式，实践中需要根据具体问题选择合适的剪枝方法。

2.2.1预剪枝

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能的提升，则停止划分并将当前结点标记为叶节点，其类型标记为当前结点数据集中总数最多的类别。

预剪枝可以时决策树很多分支不进行展开，降低了过拟合的风险，同时还显著减少了决策树的训练时间开销和测试时间开销。但另一方面，有些分支的当前划分虽然不能提升泛化性能，甚至可能导致泛化性能下降，但在其基础上进行的后续划分却有可能导致泛化性能显著提升。预剪枝基于贪心本质禁止这些分支展开，给预剪枝决策树带来了欠拟合的风险。

2.2.2后剪枝

后剪枝是先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换成叶节点能带来决策树泛化性能的提升，则将该子树替换为叶节点。

后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树。但是后剪枝过程是在生成完全决策树之后进行的，并且自底向上地对树中的所有非叶节点进行逐一考察，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多，也就算法的时间复杂度往往比较大。

2.2.3 剪枝原理的介绍

I损失函数

损失函数计算公式如下：

??????????????

其中T是任意子树，C(T)为子树的预测误差，分类树用基尼指数，回归树用均方误差。

|T|是子树T的叶子节点个数，a是正则化参数，用来平衡决策树的预测准确度和树的复杂度。

a越大，表示惩罚越大，在求最小化损失函数Ca(T)时，要求子树的叶子节点个数越少，表示树越简单，剪枝越厉害。a越小，表示树越复杂。

II?误差增加率

1)?从整体树的任意内部节点t开始。

2)?以t为单节点的树的损失为：

????????????????

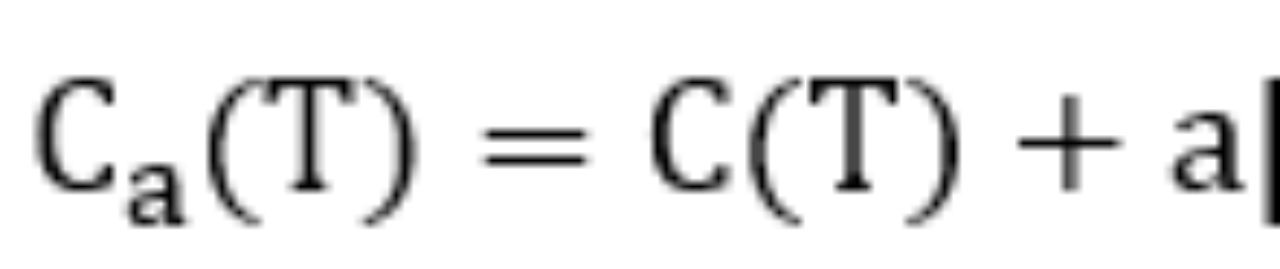
3)?以t为根节点的树的损失为：

???????????????

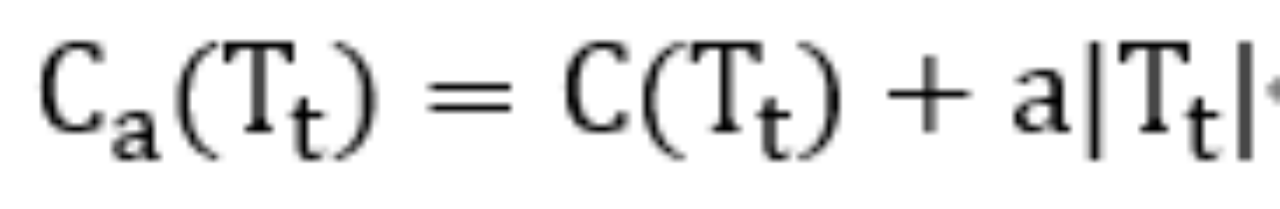
4)?如果Tt与t有同样的损失，且t的节点更少，那么t比Tt更可取，所以剪掉Tt，此时有Ca(t)=Ca(Tt)，根据2)和3)变形得：

?????????????????

这表示剪枝后整体损失函数增加的程度。其中C(t)表示节点t的子树被剪枝之后节点t的误差，C(Tt)表示节点t的子树没有被剪枝时子树Tt的误差。

C(t)=c(t)*p(t)，c(t)是节点的误差率，p(t)是节点上的数据占所有数据的比例。

剪枝之后决策树的叶子减少了|Tt|-1，|Tt|为子树Tt的叶子数。

三、数据集描述及代码实现

3.1数据集描述

我们使用?cart_tree_ex2.txt?数据集创造回归树，使用cart_tree_ex2test.txt?做测试集进行剪枝。如下所示（仅展示部分数据）：

3.2 代码实现

数据集来自网络，本次实验对其进行复现

from?numpy?import?*
import?matplotlib.pyplot?as?plt
import?matplotlib
import?re
import?copy
import?matplotlib.font_manager?as?fm


#?设置字体
plt.rcParams['font.family']?=?['Arial?Unicode?MS']

#?显示支持的中文字体
for?font?in?fm.fontManager.ttflist:
????if?'CJK'?in?font.name:
????????print(font.name)

def?loadDataSet(fileName):??#?加载数据集
????dataMat?=?[]
????fr?=?open(fileName)
????for?line?in?fr.readlines():
????????curLine?=?line.strip().split('\t')
????????fltLine?=?list(map(float,?curLine))??#?加上list就是完整功能了，不然只用map会生成内存地址
????????dataMat.append(fltLine)
????dataMat?=?array(dataMat)??#?转化为array数组，便于计算
????return?dataMat


def?binSplitDataSet(dataSet,?feature,?value):??#?把数据集根据变量(特征)feature按照切分点value分为两类
????mat0?=?dataSet[nonzero(dataSet[:,?feature]?<=?value)[0],?:]??#?大于成为左子树，
????mat1?=?dataSet[nonzero(dataSet[:,?feature]?>?value)[0],?:]
????return?mat0,?mat1


def?regLeaf(dataSet):??#?计算平均值，负责生成叶子节点，叶子节点根据公式不就是求所在子区域的平均值
????return?mean(dataSet[:,?-1])


def?regErr(dataSet):??#?方差×个数?=?每个点与估计值的差的平方和，这是根据损失函数公式来的
????return?var(dataSet[:,?-1])?*?shape(dataSet)[0]


def?chooseBestSplit(dataSet,?leafType=regLeaf,?errType=regErr,?ops=(1,?2)):
????tols?=?ops[0]??#?最小下降损失是1
????tolN?=?ops[1]??#?最小样本数是4
????if?len(set(dataSet[:,?-1]))?==?1:??#?停止切分的条件之一
????????return?None,?leafType(dataSet)
????m,?n?=?shape(dataSet)
????S?=?errType(dataSet)
????bestS?=?inf??#?最优切分点的误差
????bestIndex?=?0??#?最优切分变量的下标
????bestValue?=?0??#?最优切分点
????for?featIndex?in?range(n?-?1):??#?遍历除最后一列的其他特征，我们的数据集是（x,y），因此这里只能遍历x
????????for?splitVal?in?set(dataSet[:,?featIndex]):??#?splitVal是x可能去到的每一个值作为切分点
????????????mat0,?mat1?=?binSplitDataSet(dataSet,?featIndex,?splitVal)??#?根据切分点划分为两个子区域
????????????if?(shape(mat0)[0]?<?tolN)?or?(shape(mat1)[0]?<?tolN):??#?如果两个子区域的叶子节点小于4个，跳过此切分点
????????????????#?print("内层判别小于4___________________")
????????????????#?print(shape(mat0)[0],shape(mat1)[0])
????????????????continue
????????????newS?=?errType(mat0)?+?errType(mat1)??#?计算两部分的损失函数
????????????if?newS?<?bestS:??#?如果损失函数小于最优损失函数
????????????????bestIndex?=?featIndex??#?最优切分变量保存起来
????????????????bestValue?=?splitVal??#?最优切分点保存起来
????????????????bestS?=?newS??#?最优损失函数保存起来
????if?(S?-?bestS)?<?tols:??#?如果切分之前的损失减切分之后的损失小于1,那么就是切分前后损失减小的太慢，停止.它是主要的停止条件
????????return?None,?leafType(dataSet)
????mat0,?mat1?=?binSplitDataSet(dataSet,?bestIndex,?bestValue)??#?按照最优切分点分成两个区域
????if?(shape(mat0)[0]?<?tolN)?or?(shape(mat1)[0]?<?tolN):??#?如果任何一个子区域的样本数小于4个，停止切分
????????#?print("外层判断切分样本数小于4******************")???????#?个人感觉此判断没用，因为上面选择切分点的时候就把这个情况删除了
????????return?None,?leafType(dataSet)

????return?bestIndex,?bestValue


def?createTree(dataSet,?leafType=regLeaf,?errType=regErr,?ops=(1,?4)):
????feat,?val?=?chooseBestSplit(dataSet,?leafType,?errType,?ops)??#?最优切分点切分
????if?feat?==?None:??#?如果是叶子节点，那么val是那个数据集的平均值，即c
????????#?print("NOne/执行了",val)
????????return?val
????#?print("没执行",val)
????retTree?=?{}
????retTree['spInd']?=?feat??#?最优切分变量(特征)的下标值
????retTree['spVal']?=?val??#?最优切分点s，假如执行到这里，说明找到了最优切分点，将继续切分
????lSet,?rSet?=?binSplitDataSet(dataSet,?feat,?val)??#?切分成两个子区域，lSet是大于切分点的，相当于我们图形的右边
????retTree['left']?=?createTree(lSet,?leafType,?errType,?ops)??#?左子树继续切分
????retTree['right']?=?createTree(rSet,?leafType,?errType,?ops)??#?右子树继续切分
????return?retTree


#?------------------------------------?剪枝处理?----------------------------------------

def?isTree(obj):
????return?(type(obj).__name__?==?'dict')??#?判断是叶子还是树
def?getMean(tree):
????if?isTree(tree['left']):
????????tree['left']?=?getMean(tree['left'])
????if?isTree(tree['right']):
????????tree['right']?=?getMean(tree['right'])
????return?(tree['left']?+?tree['right'])?/?2.0


def?prune(tree,?testData):??#?剪枝
????if?shape(testData)[0]?==?0:
????????print("判断测试集为空,执行过吗？")
????????return?getMean(tree)
????if?(isTree(tree['left'])?or?isTree(tree['right'])):
????????lSet,?rSet?=?binSplitDataSet(testData,?tree['spInd'],?tree['spVal'])
????if?isTree(tree['left']):
????????tree['left']?=?prune(tree['left'],?lSet)
????if?isTree(tree['right']):
????????tree['right']?=?prune(tree['right'],?rSet)
????if?not?isTree(tree['left'])?and?not?isTree(tree['right']):
????????lSet,?rSet?=?binSplitDataSet(testData,?tree['spInd'],?tree['spVal'])
????????errorNoMerge?=?sum(power(lSet[:,?-1]?-?tree['left'],?2))?+?sum(power(rSet[:,?-1]?-?tree['right'],?2))
????????treeMean?=?(tree['left']?+?tree['right'])?/?2.0
????????errorMerge?=?sum(power(testData[:,?-1]?-?treeMean,?2))
????????if?errorMerge?<?errorNoMerge:
????????????print("merging")
????????????return?treeMean
????????else:
????????????return?tree
????else:
????????return?tree


def?reExtract(retTree_str):??#?正则提取
????x_division_str?=?"'spVal':?(\d+\.?\d*)"??#?正则提取出切分节点
????y_estimate_str?=?"'left':?(-?\d+\.?\d*)|'right':?(-?\d+\.?\d*)"??#?正则表达式取出来叶子节点数据，即最优估计值
????x_division?=?re.compile(x_division_str).findall(retTree_str)
????y_estimate?=?re.compile(y_estimate_str).findall(retTree_str)

????x_division?=?sort(list(map(float,?x_division)))??#?切分点排序，因为我们画图都是从左往右画，正好对应下面的最优估计值c
????y_estimate?=?[float(x)?for?y?in?y_estimate?for?x?in?y?if?x?!=?'']??#?估计值的顺序不能乱，树中的是什么顺序就是什么顺序
????return?x_division,?y_estimate


def?drawPicture(dataSet,?x_division,?y_estimate,?title_name):??#?x_division是切分点，y_estimate是估计值
????fig?=?plt.figure()??#?创建画布
????ax?=?fig.add_subplot(111)
????points_x?=?dataSet[:,?0]??#?因为咱们的数据是(x,y)二维图形，x是切分变量，y是估计变量，可参照博客中的具体实例加以理解
????points_y?=?dataSet[:,?1]

????x_min?=?min(points_x)??#?创造切分区域，所以需要x的最小值和最大值，从而构造区域
????x_max?=?max(points_x)
????y_estimate.append(y_estimate[-1])

????ax.step([x_min]?+?list(x_division)?+?[x_max],?y_estimate,?where='post',?c='green',?linewidth=4,
????????????label="最优估计值")??#?画最优估计值
????ax.scatter(points_x,?points_y,?s=30,?c='red',?marker='s',?label="样本点")??#?画样本点
????ax.legend(loc=4)??#?添加图例
????#?ax.grid()???????????????#?添加网格
????ax.set_yticks(y_estimate)??#?设置总坐标刻度
????ax.set_xlabel("x")
????ax.set_ylabel("y")
????ax.set_title(title_name)

????plt.show()


#?------------------------------------------画树状图---------------------------------------

def?getTreeLeafNum(tree):??#?得到叶子数
????global?numLeafs
????key_list?=?['left',?'right']
????for?key?in?key_list:
????????if?isTree(tree[key]):
????????????getTreeLeafNum(tree[key])
????????else:
????????????numLeafs?+=?1
????return?numLeafs


def?getTreeDepth(tree):??#?得到树的深度
????max_depth?=?0
????key_list?=?['left',?'right']
????for?key?in?key_list:
????????if?isTree(tree[key]):
????????????depth?=?1?+?getTreeDepth(tree[key])
????????else:
????????????depth?=?1
????????if?depth?>?max_depth:
????????????max_depth?=?depth
????return?max_depth


def?plotNode(ax,?str,?xy_point,?xytext_points):??#?画节点
????ax.annotate(str,?xy=xy_point,?xytext=xytext_points,?va="center",?ha="center",?arrowprops=dict(arrowstyle="<-"),
????????????????bbox=dict(boxstyle="square",?color="red",?alpha=0.3))


def?plotLeaf(ax,?str,?xy_point,?xytext_points):??#?画叶子
????ax.annotate(str,?xy=xy_point,?xytext=xytext_points,?va="center",?ha="center",?arrowprops=dict(arrowstyle="<-"),
????????????????bbox=dict(boxstyle="round",?color="green",?alpha=0.6))


def?midText(ax,?annotation_location,?xy_location,?content_str):??#?画中间注释
????x?=?(xy_location[0]?-?annotation_location[0])?/?2?+?annotation_location[0]
????y?=?(xy_location[1]?-?annotation_location[1])?/?2?+?annotation_location[1]
????ax.text(x,?y,?content_str)


def?plotTree(ax,?tree,?xy_location,?treeWidth,?treeDepth,?midtext):??#?递归画树
????global?x_offset??#?x的偏移全局变量，举个例子如果叶子共3个，那么从左到右，第一个叶子x坐标就是1/6,第二个叶子x坐标是3/6,第三个是5/6
????global?y_offset??#?画一次这个总坐标就降1/总深度

????leaf_num?=?getTreeLeafNum(tree)??#?叶子数
????global?numLeafs
????numLeafs?=?0
????depth?=?getTreeDepth(tree)??#?深度
????annotation?=?round(tree['spVal'],?2)
????annotation_location?=?(x_offset?+?(1.0?+?float(leaf_num))?/?2.0?/?treeWidth,?y_offset)??#?它是节点的注释位置，却是叶子的箭头位置
????#?midText(ax,annotation_location,xy_location,midtext)
????plotNode(ax,?annotation,?xy_location,?annotation_location)??#?画节点
????y_offset?=?y_offset?-?1.0?/?treeDepth
????key_list?=?['left',?'right']
????for?key?in?key_list:
????????if?type(tree[key]).__name__?==?'dict':
????????????#?print("x_off:{0}\ny_off:{1}".format(x_offset,y_offset))
????????????plotTree(ax,?tree[key],?annotation_location,?treeWidth,?treeDepth,?str(key))??#?递归
????????else:
????????????x_offset?=?x_offset?+?1.0?/?treeWidth??#?画一个叶子x_offset往右移动1/叶子总数
????????????#?print("x_off:{0}\ny_off:{1}-----------".format(x_offset,y_offset))
????????????plotLeaf(ax,?round(tree[key],?2),?annotation_location,?(x_offset,?y_offset))??#?画叶子
????????????#?midText(ax,(x_offset,y_offset),annotation_location,str(key))
????y_offset?=?y_offset?+?1.0?/?treeDepth??#?递归完一次，总坐标y_offset需要增加一个1/总深度，即这时s形画，再回去


def?createPlot(tree,?title_name):??#?画决策树
????fig?=?plt.figure()
????ax?=?fig.add_subplot(111,?frameon=False)??#?边框去掉

????tree_width?=?getTreeLeafNum(tree)??#?树的叶子数
????global?numLeafs
????numLeafs?=?0
????tree_depth?=?getTreeDepth(tree)??#?树的深度
????global?x_offset
????x_offset?=?-0.5?/?tree_width??#?起始x偏移为-1/(2*叶子数)
????global?y_offset
????y_offset?=?1.0??#?起始y偏移为1

????plotTree(ax,?tree,?(0.5,?1.0),?tree_width,?tree_depth,?"")

????ax.set_xticks([])
????ax.set_yticks([])??#?坐标刻度清除
????ax.set_title(title_name)
????plt.show()


if?__name__?==?'__main__':
????global?numLeafs??#?定义全局变量，便于计算一棵树的总叶子数
????numLeafs?=?0

????global?x_offset??#?用于画注解树
????x_offset?=?0
????global?y_offset
????y_offset?=?0
????#?dataset?=?loadDataSet('/home/zhangqingfeng/test/cart_tree/cart_tree.txt')??#?加载训练集
????myData?=?loadDataSet('cart_tree_ex2.txt')??#?加载测试集
????mytestData?=?loadDataSet('cart_tree_ex2test.txt')
????#?first_tree?=?createTree(dataset,ops=(1,4))
????#?createPlot(first_tree,"")
????InialTree?=?createTree(myData,?ops=(100,?4))??#?创建训练集的树
????print("裁剪前的回归树为：",?InialTree)
????createPlot(InialTree,?"剪之前的决策树")??#?画出剪之前的决策树
????InialTree_str?=?str(InialTree)
????x_d,?y_e?=?reExtract(InialTree_str)
????drawPicture(mytestData,?x_d,?y_e,?"剪之前的拟合")??#?画出剪枝之前的拟合阶梯函数

????prune_tree?=?prune(InialTree,?mytestData)??#?通过测试集对树进行剪枝

????createPlot(prune_tree,?"剪之后的决策树")??#?画出剪枝后的决策树
????retTree_str?=?str(prune_tree)??#?转化为字符串好用正则
????print("裁剪后的回归树为:?",?retTree_str)
????x_division,?y_estimate?=?reExtract(retTree_str)
????drawPicture(mytestData,?x_division,?y_estimate,?"剪之后的拟合")??#?画出剪枝后的拟合阶梯函数

3.3?运行结果

（1）剪枝前的拟合

（2）剪之前的决策树

（3）剪之后的拟合

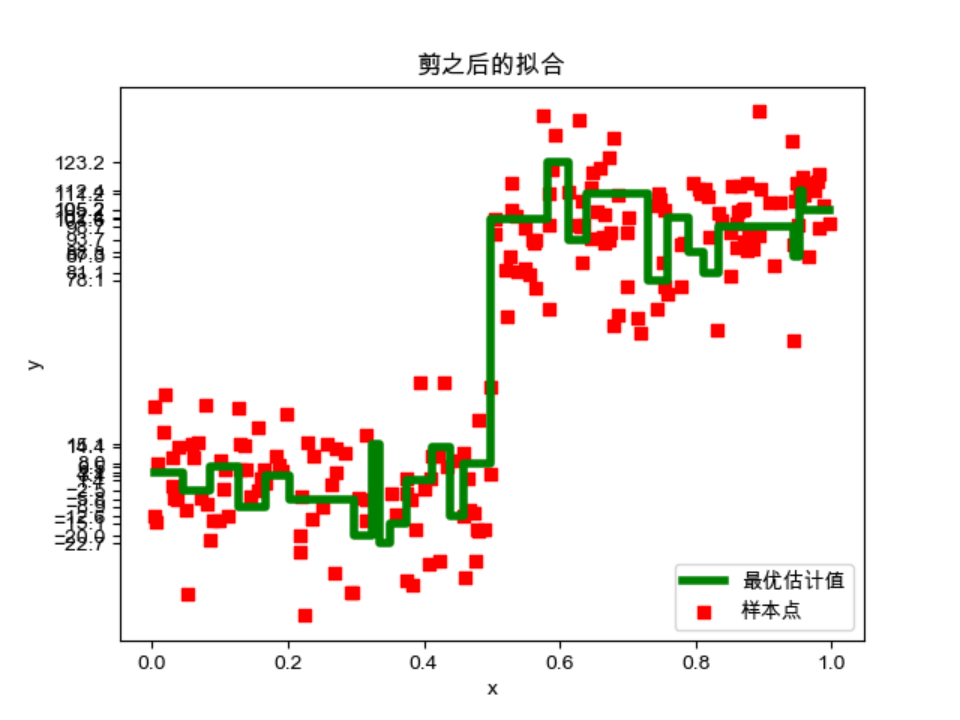
（4）剪之后的决策树

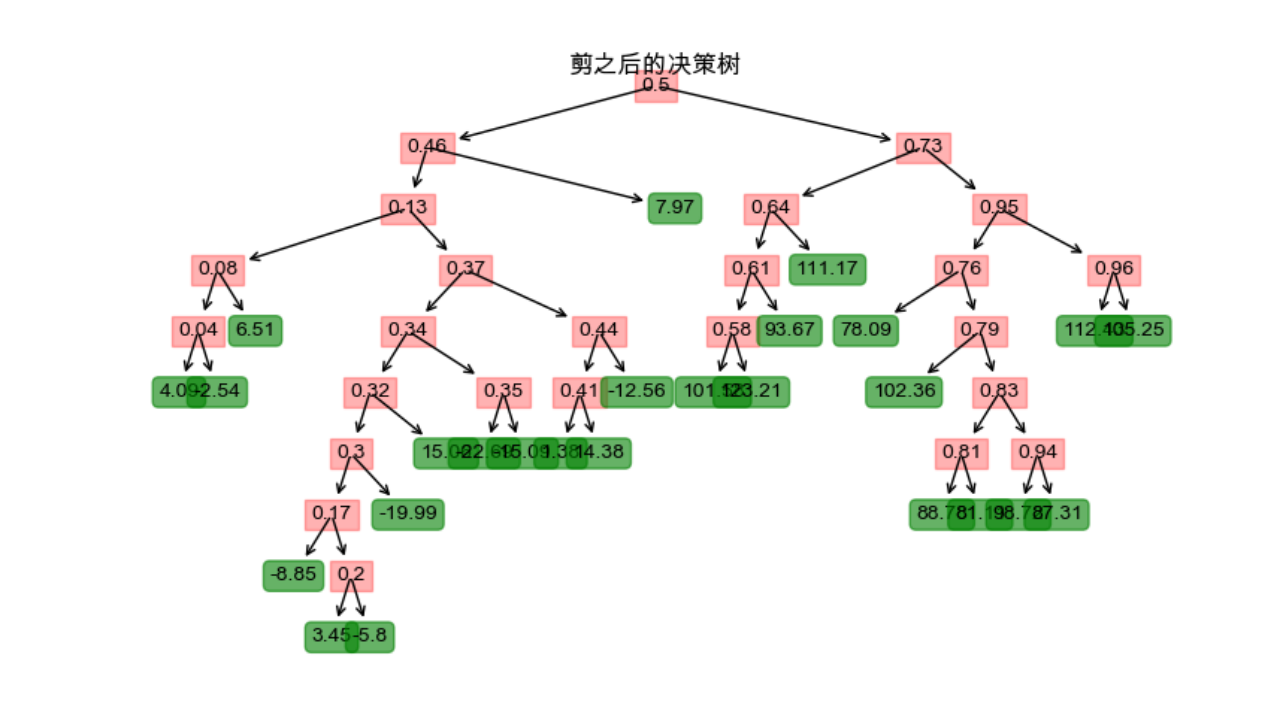
观察实验结果后可知

I?剪枝可以有效地去除过拟合的部分，从而提高模型对未见过数据的泛化能力。

II?剪枝会减少模型的复杂度，使得决策树更加简洁易懂，减少了决策树的分支和叶节点数量。

III剪枝后的决策树结构更加简化，易于解释和理解。

即提高了模型泛化能力，使模型更简洁、可解释性更好。

四、实验讨论

4.1 CART算法与ID3算法、C4.5算法的比较

（1）划分标准的差异：?ID3?使用信息增益偏向特征值多的特征，C4.5?使用信息增益率克服信息增益的缺点，偏向于特征值小的特征，CART?使用基尼指数克服?C4.5?需要求?log?的巨大计算量，偏向于特征值较多的特征。

（2）使用场景的差异：?ID3?和?C4.5?都只能用于分类问题，CART?可以用于分类和回归问题；ID3?和?C4.5?是多叉树，速度较慢，CART?是二叉树，计算速度很快；

（3）样本数据的差异：?ID3?只能处理离散数据且缺失值敏感，C4.5?和?CART?可以处理连续性数据且有多种方式处理缺失值；从样本量考虑的话，小样本建议?C4.5、大样本建议?CART。C4.5?处理过程中需对数据集进行多次扫描排序，处理成本耗时较高，而?CART?本身是一种大样本的统计方法，小样本处理下泛化误差较大；

（4）样本特征的差异：?ID3?和?C4.5?层级之间只使用一次特征，CART?可多次重复使用特征；

（5）剪枝策略的差异：?ID3?没有剪枝策略，C4.5?是通过悲观剪枝策略来修正树的准确性，而?CART?是通过代价复杂度剪枝。

4.2CART算法优缺点

CART（分类回归树）算法是一种经典的决策树算法，它具有以下优缺点：

（1）优点：

灵活性：CART算法可以处理离散型和连续型特征，能够对非线性关系建模，适用于多种类型的数据。

可解释性：CART算法生成的决策树易于理解和解释，可以提供关于数据集特征的重要信息。

数据预处理要求低：CART算法具有较强的容错性，能够处理大规模、高纬度、带缺失值的数据集。

生成子决策树的过程可以并行化处理。

（2）缺点：

易过拟合：CART算法的生成过程是自顶向下的贪心算法，容易陷入局部最优解，在训练集上会表现得过于复杂，导致过拟合问题。

对输入数据的变化敏感：CART算法生成的决策树比较脆弱，对于数据分布的微小变化，都可能导致生成的决策树发生较大的变化。

难以处理类别不平衡的数据集：CART算法在划分过程中，使用的是简单的基于不纯度的准则，未考虑类别不平衡的情况，容易导致生成的决策树偏向于数量较多的类别。

准确性较低：与其他机器学习算法相比，CART算法的预测准确率相对较低。

总的来说，CART算法具有可解释性强、数据预处理要求低等优点，但也存在易过拟合、对输入数据的变化敏感、难以处理类别不平衡数据集等缺点。对于这些缺点，可以采用剪枝、集成学习等方法进行改进。

4.3关于CART分类树与决策树

（1）CART分类树：

在CART分类树中，该算法通过递归地将数据集划分成子集，直到达到预定的停止条件。在每个节点上，CART算法选择最优的特征作为划分标准，基于某个不纯度指标（如基尼系数）来评估特征的重要性。通过计算该特征的增益或基尼系数减少来选择最佳的划分点。接下来，根据划分点将数据集分成两个子集，然后对每个子集递归地进行划分，直到满足停止条件，例如达到预定义的树深度、节点中样本数量小于某个阈值等。叶节点上的样本将被分配给具有该类别最多的类或具有最高概率的类别。

（2）CART回归树：

CART回归树与CART分类树的思想非常类似，但是用于解决回归问题。与分类树不同的是，回归树的叶节点上的预测值不是离散的类别标签，而是一个连续的数值。在每个节点上，CART算法通过最小化平方误差或均方误差（MSE）来选择最佳的划分特征和划分点。回归树的生成过程与分类树类似，递归划分数据集，直到满足停止条件。

无论是CART分类树还是回归树，在学习过程中使用了相似的划分策略，并且都具有较好的解释性和灵活性。它们可以通过对数据集进行递归划分来构建决策树模型，并能够进行预测和解释分类或回归任务的结果。

4.4 CART算法的改进

CART算法一般采用基于最小化Gini指数的贪心策略进行节点分裂，因此其容易陷入局部最优解，并且对数据噪声比较敏感。为了改进CART算法的性能，可以使用以下几种方法：

改进节点分裂准则：传统的CART算法使用基尼指数作为节点分裂准则，但也可以考虑使用其他指标，例如信息增益、信息增益比和均方误差等。这些指标在不同场景下可能会有更好的性能表现。

集成学习方法：可以采用Bagging、Boosting等集成学习方法来提升CART算法的泛化性能，例如随机森林算法就是通过Bagging方法改进的决策树算法。

剪枝方法：对建立好的决策树进行剪枝可以缓解过拟合问题，在验证集上选择最优的剪枝方式可以进一步提高泛化性能。

数据预处理：CART算法对于异常值、缺失值等数据噪声比较敏感，因此需要进行相应的数据预处理工作。

改善类别不平衡问题：对于类别不平衡的数据集，可以采用过抽样、欠抽样和基于代价敏感学习等方法进行改进。

总之，CART算法在实践中可以通过调节模型参数、采用集成学习等方法进行改进，以提升其分类/回归性能。

五、算法总结

CART算法是一种经典的决策树算法，它可以用于分类和回归问题。CART算法通过选择最优的分裂准则来进行数据划分，常用的准则包括基尼指数、信息增益、信息增益比和均方误差等。不同的分裂准则会导致不同的决策树结构和分类/回归性能，因此选择合适的分裂准则非常重要。

与其他决策树算法相比，CART算法具有灵活性、可解释性强、数据预处理要求低等优点。但也存在易过拟合、对输入数据的变化敏感、难以处理类别不平衡数据集等缺点。对于这些缺点，可以采用剪枝、集成学习等方法进行改进。

2024-1-21

文章来源:https://blog.csdn.net/m0_64198455/article/details/135731103
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！