MIT_线性代数笔记：第 20 讲 克莱姆法则、逆矩阵、体积

我们已经了解了行列式的公式和性质，下面讨论它的应用。

逆矩阵的公式 Formula for $A^{?1}$

我们已经知道二阶矩阵的逆矩阵公式：
$$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=\frac{1}{ad?bc}\left[\begin{array}{cc}d& ?b\\ ?c& a\end{array}\right]$$
那么我们能写出三阶甚至高阶的公式么？通过观察二阶矩阵逆矩阵的公式，我们可以用同样的策略来构造高阶矩阵的求逆公式，为：
$$A^{?1}=\frac{1}{det(A)}{C}^{{}_T}$$
矩阵外因子的分母是矩阵的行列式的值，而矩阵是“代数余子式矩阵”（cofactor matrix）C 的转置矩阵 C T。即伴随矩阵（adjoint matrix）。
矩阵 A 的行列式的计算中包含的都是 n 个元素的乘积：

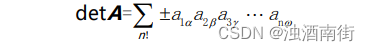
而伴随矩阵中的元素都是 n-1 阶行列式，它的运算中出现的是 n-1 个矩阵 A 中元素的乘积。所以矩阵 A 与两者相乘才能完全消去，而得到单位矩阵。下面我们就用矩阵 A 与矩阵 $C^{{}_T}$相乘来验证 A$C^{{}_T}$ =det(A)I，并且理解逆矩阵的构造策略。

矩阵 AC T 第一行第一列的元素等于矩阵 A 第一行和矩阵 C T 第一列进行点积，计算可得：

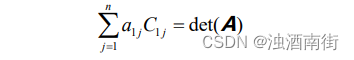
点积的算式本身就是矩阵 A 的计算公式，因此结果为 A 行列式的值。而矩阵A$C^{{}_T}$ 对角线上所有的元素都是如此，因此其对角戏上的元素都等于 detA。
而对于非对角线元素，我们以第二行第一列的元素为例，其计算公式为：

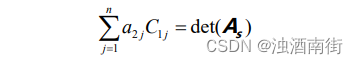
这可以视为矩阵 As 的行列式数值，各个代数余子式的形式不变，但是与代数余子式相乘的变为了矩阵 A 第二行第 j 列元素。因此 As 的形式相当于用矩阵 A 第二行的元素替代第一行的元素得到的矩阵。因为该矩阵中前两行完全相同，因此按照行列式性质 4，det(As)=0；

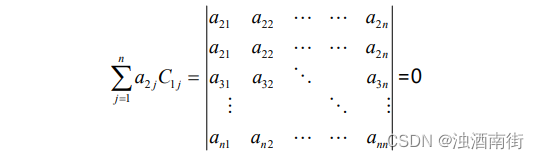
而 AC T乘积矩阵中非对角线元素的计算均服从此规律，因此均为 0。则：

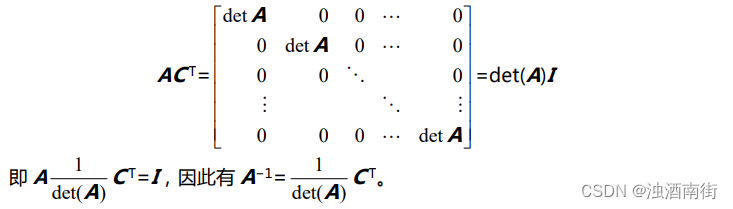
逆矩阵公式的一个好处就是，我们从中可以看到，当改变原矩阵中的一个元素时，给逆矩阵带来了怎样的变化。

克莱姆法则 Cramer’s Rule for x = $A^{?1}$b

对于可逆矩阵 A，方程 Ax=b 必然有解 x=$A^{?1}$b，将逆矩阵的公式带入其中，则有：

矩阵 $B_j$的行列式的数值从第 j 列用代数余子式进行展开计算，正好是伴随矩阵 $C^T$的第 j 行与向量 b 点积的结果。此处我们用到了行列式的性质 10。 相比于消元法，采用克莱姆法则计算方程的解效率较低。

体积 |det(A)|=volume of box

矩阵 A 行列式的绝对值等于以矩阵 A 行（列）向量为边所构成的平行六面体的体积。行列式的正负对应左手系和右手系。之前提到过行列式是将矩阵的信息压缩成一个数，可以将“体积”视为它压缩后给出的信息。
如果矩阵 A 是单位矩阵，则其构成的是三个边长均为 1 且互相垂直的立方体，其体积为 1，这与上面的结论相符。这也是行列式的性质 1。
而如果矩阵 A 为正交矩阵 Q，则其构成的也是三个边边长为 1 且三边互相垂直的立方体，其体积也为 1 只是取向与单位阵不同。这也与上面的结论相符，因为$Q^T$Q=I，且 detQ=det$Q^T$，所以 detQ= $\pm$ 1。
交换矩阵 A 中的行并不会改变其行列式的绝对值，显然也不会改变向量围成的体积，因此这也和体积理论相符。这是行列式的性质 2。

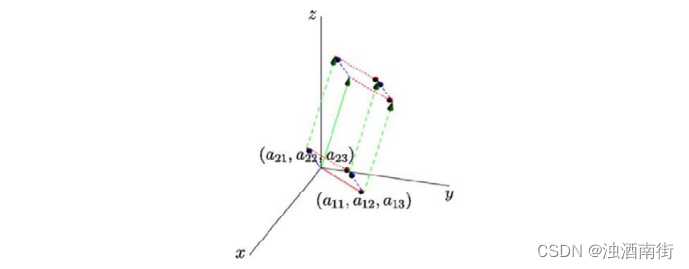
对于长方体，也非常直观，当你将其中一条边的边长增加 2 倍时，正方体的体积也会增加 2 倍成为长方体，这相当于性质 3a。
对于性质 3b，我们可以在二维条件下简单证明。



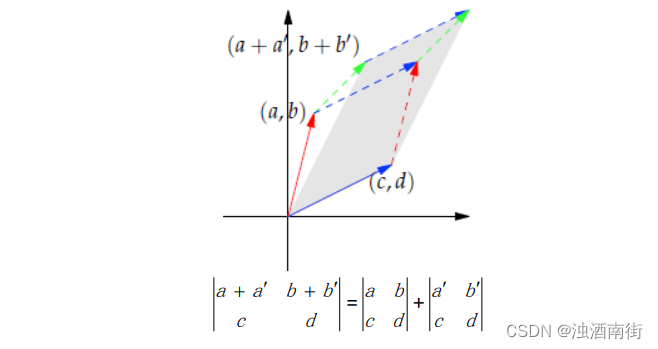
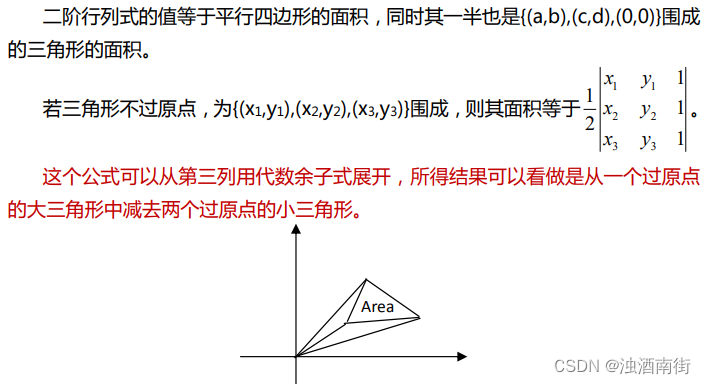
除以上各条之外，性质 4 也比较直观，当有两条边重合时，平行六面体或者平行四边形被压扁，体积或者面积为 0。