2024华数杯B题高质量成品论文22页+可执行matlab+py代码+讲解视频+论文修改+运行结果对照表

1 第一问模型的建立与求解? （完整版的见文末）

数据表格将包括以下列：

(1)??年份

(2)??总用电量（万亿千瓦时）

(3)??火电装机容量（千瓦）

(4)??风电装机容量（千瓦）

(5)??太阳能装机容量（千瓦）

(6)??水电装机容量（千瓦）

(7)??非化石能源比重

(8)??工业部门电气化率

(9)??建筑部门电气化率

(10) 交通部门电气化率

(11) 煤电装机容量（千瓦）

(12) 气电装机容量（千瓦）

(13) 核电装机容量（千瓦）

1.2 Yeo-Johnson??转换

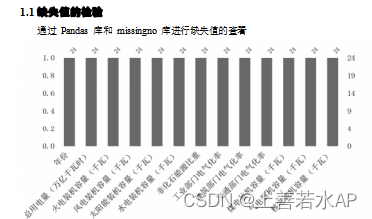
为了防止建立的模型过拟合以及提高模型的泛化能力，?需要对数据的分布情况进行?探索分析，力求保证数据集分布情况一致，首先将数据导入，运用?Python?判断每一列?数据的分布类型是否属于正态分布，本代码通过 SciPy ?库中的 stats.skew（）?函数来 判断数据是否需要进行 Yeo-Johnson ?转换。Skewness（即偏度） 是衡量某一个样本数值?相对于平均数的偏离程度的统计量， 它可以用来描述数据的分布形态是否对称。偏度为?0 ?表示数据分布是对称的， 偏度大于 0??表示数据分布偏向右侧， 偏度小于?0??表示数据?分布偏向左侧

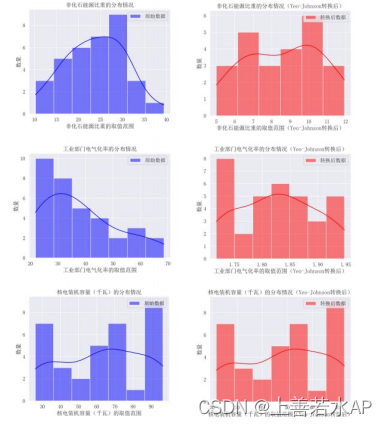
在本代码中， 如果数据的偏度值的绝对值大于某个非常小的阈值 0.05，则表示该数?据分布类型不是正态分布， 需要进行 Yeo-Johnson ?转换，?下图仅展示部分特征的原始数?据直方图分布和对应的?Yeo-Johnson ?转换后的直方图。

然后将随机森林和梯度提升树取平均值可以得到更稳健的结果。

1. ???随机森林求特征重要性： 随机森林是一种集成学习方法， 它将多个决策树组合起来，?每个树都随机选择部分特征进行训练。通过测量在随机森林中每个特征的重要性，?我们可以获得一个特征重要性的排名。在随机森林中，?特征重要性是根据袋外误差?（Out-Of-Bag Error）进行计算的，?袋外误差是指在训练随机森林时，?每个决策树中?未被选中的样本数据。

2. ???GBDT 求特征重要性：?梯度提升树是另一种常见的集成学习方法，?它通过不断地迭?代生成一组决策树来拟合数据，?每棵树都会根据上一棵树的预测误差进行训练。在?GBDT?中，特征重要性是通过测量每个特征在训练过程中平均分裂增益（Mean Split?Gain）来计算的，?即在每个节点上选择哪个特征作为分裂点，?以达到最大的信息增?益。

3. ???取平均值：?对于每个特征， 我们可以通过随机森林和?GBDT?得到两个不同的特征重?要性排名。为了得到更稳健的结果，?我们可以将两种方法得到的特征重要性取平均?值，以此作为最终的特征重要性排名。

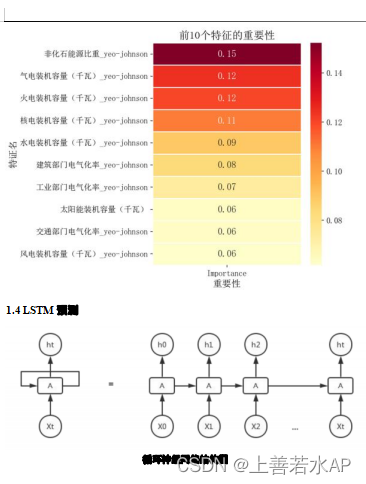
这种方法的好处包括：

1. ???随机森林和?GBDT?都是常见的机器学习方法，它们在不同的领域都有广泛的应用。?因此，这种方法可以适用于各种类型的数据和问题。

2. ???通过使用两种不同的方法计算特征重要性， 我们可以避免单一方法带来的误差和偏?差，从而得到更准确和可靠的特征重要性排名。

3. ???通过取平均值，?我们可以得到更稳健的结果。因为两种方法都有自己的优点和局限?性，它们可以相互补充，提高特征重要性的可信度和可解释性。

计算结果如下：

全网最正确〕2024华数杯B题成品论文52页word+四小问可执行代码+代码调式+结果分析+高清运行结果图