Java快速排序希尔排序归并排序
发布时间:2024年01月07日
快速排序算法
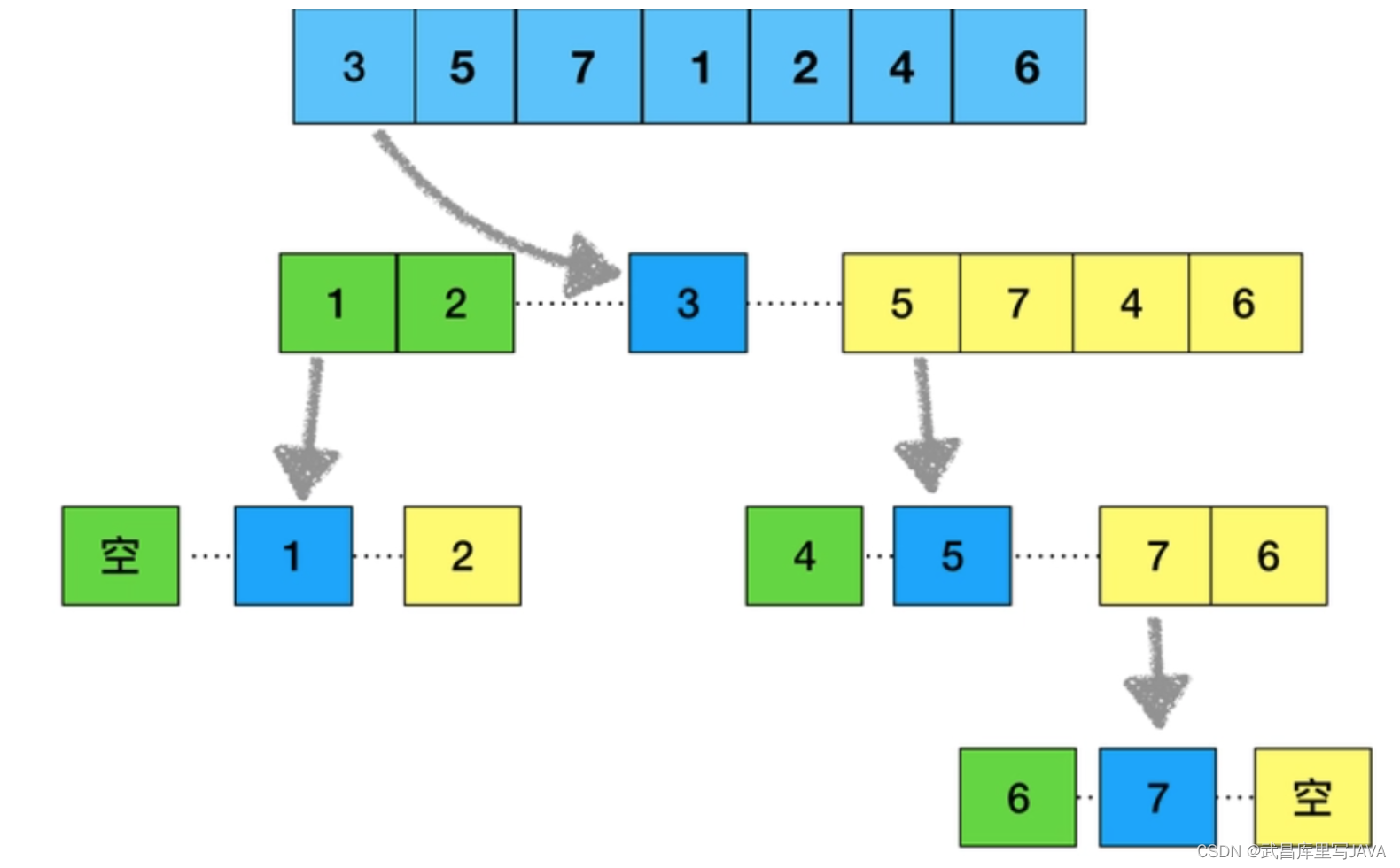
快速排序的原理:选择一个关键值作为基准值。比基准值小的都在左边序列(一般是无序的),比基准值大的都在右边(一般是无序的)。一般选择序列的第一个元素。
一次循环:从后往前比较,用基准值和最后一个值比较,如果比基准值小的交换位置,如果没有继续比较下一个,直到找到第一个比基准值小的值才交换。找到这个值之后,又从前往后开始比较,如果有比基准值大的,交换位置,如果没有继续比较下一个,直到找到第一个比基准值大的值才交换。直到从前往后的比较索引>从后往前比较的索引,结束第一次循环,此时,对于基准值来说,左右两边就是有序的了。
public void sort(int[] a, int low, int high) {
int start = low;
int end = high;
int key = a[low];
while (end > start) {
//从后往前比较
while (end > start && a[end] >= key)
//如果没有比关键值小的,比较下一个,直到有比关键值小的交换位置,然后又从前往后比较
end--;
if (a[end] <= key) {
int temp = a[end];
a[end] = a[start];
a[start] = temp;
}
//从前往后比较
while (end > start && a[start] <= key)
//如果没有比关键值大的,比较下一个,直到有比关键值大的交换位置
start++;
if (a[start] >= key) {
int temp = a[start];
a[start] = a[end];
a[end] = temp;
}
//此时第一次循环比较结束,关键值的位置已经确定了。左边的值都比关键值小,右边的
值都比关键值大,但是两边的顺序还有可能是不一样的,进行下面的递归调用
}
//递归
if (start > low) sort(a, low, start - 1);//左边序列。第一个索引位置到关键值索引-1
if (end < high) sort(a, end + 1, high);//右边序列。从关键值索引+1 到最后一个
}
}
希尔排序算法
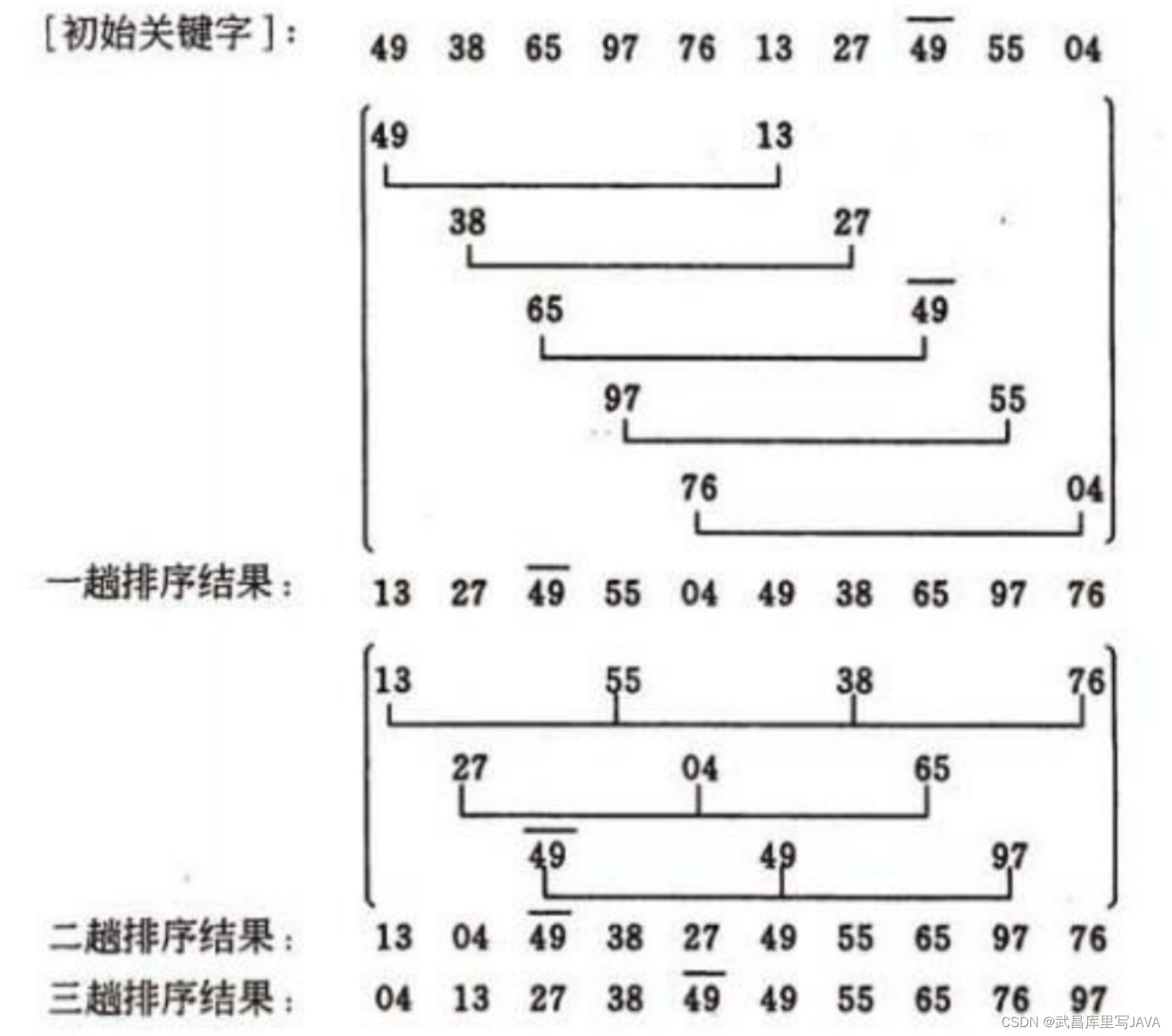
基本思想:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
-
操作方法:选择一个增量序列 t1,t2,…,tk,其中 ti>tj,tk=1;
-
按增量序列个数 k,对序列进行 k 趟排序;
-
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
private void shellSort(int[] a) {
int dk = a.length / 2;
while (dk >= 1) {
ShellInsertSort(a, dk);
dk = dk / 2;
}
}
private void ShellInsertSort(int[] a, int dk) {
//类似插入排序,只是插入排序增量是 1,这里增量是 dk,把 1 换成 dk 就可以了
for (int i = dk; i < a.length; i++) {
if (a[i] < a[i - dk]) {
int j;
int x = a[i];//x 为待插入元素
a[i] = a[i - dk];
for (j = i - dk; j >= 0 && x < a[j]; j = j - dk) {
//通过循环,逐个后移一位找到要插入的位置。
a[j + dk] = a[j];
}
a[j + dk] = x;//插入
}
}
}
归并排序算法
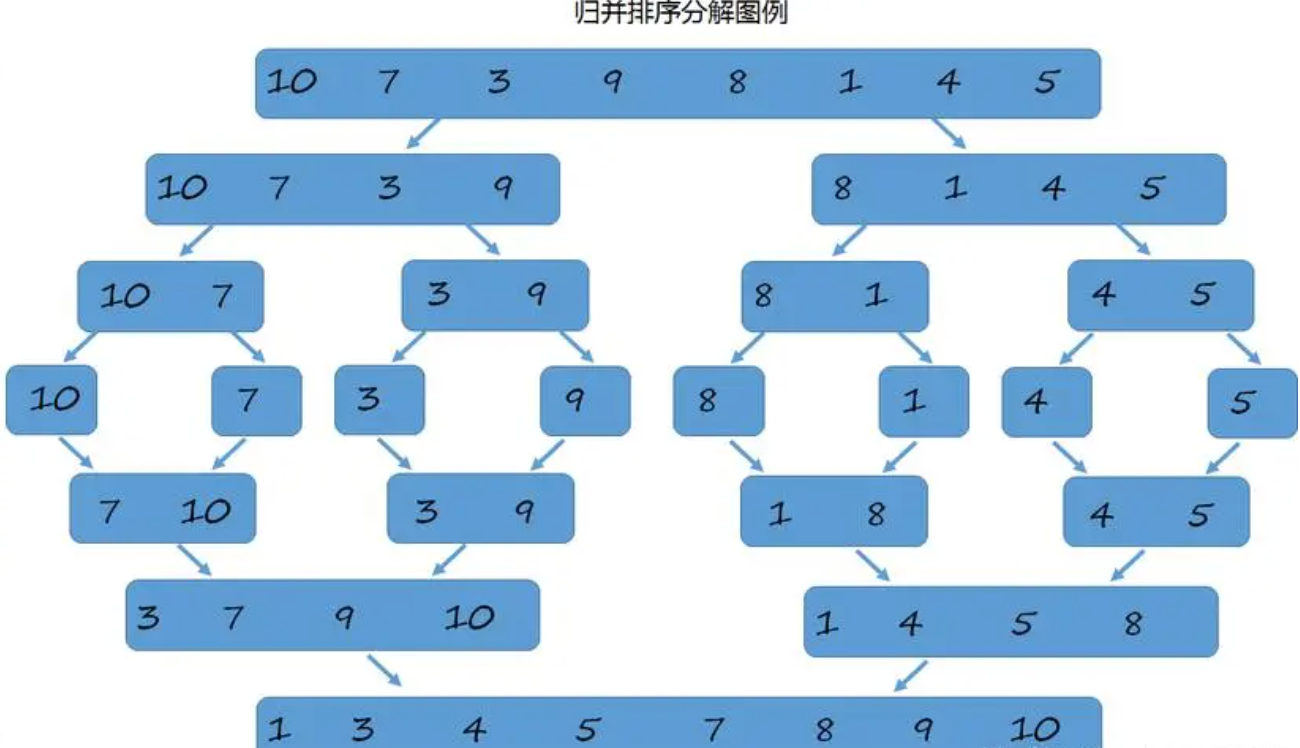
归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
public class MergeSortTest {
public static void main(String[] args) {
int[] data = new int[]{5, 3, 6, 2, 1, 9, 4, 8, 7};
print(data);
mergeSort(data);
System.out.println("排序后的数组:");
print(data);
}
public static void mergeSort(int[] data) {
sort(data, 0, data.length - 1);
}
public static void sort(int[] data, int left, int right) {
if (left >= right)
return;
// 找出中间索引
int center = (left + right) / 2;
// 对左边数组进行递归
sort(data, left, center);
// 对右边数组进行递归
sort(data, center + 1, right);
// 合并
merge(data, left, center, right);
print(data);
}
/**
* \* 将两个数组进行归并,归并前面 2 个数组已有序,归并后依然有序
* <p>
* \*
* <p>
* \* @param data
* <p>
* \* 数组对象
* <p>
* \* @param left
* <p>
* \* 左数组的第一个元素的索引
* <p>
* \* @param center
* <p>
* \* 左数组的最后一个元素的索引,center+1 是右数组第一个元素的索引
* <p>
* \* @param right
* <p>
* \* 右数组最后一个元素的索引
*/
public static void merge(int[] data, int left, int center, int right) {
// 临时数组
int[] tmpArr = new int[data.length];
// 右数组第一个元素索引
int mid = center + 1;
// third 记录临时数组的索引
int third = left;
// 缓存左数组第一个元素的索引
int tmp = left;
while (left <= center && mid <= right) {
// 从两个数组中取出最小的放入临时数组
if (data[left] <= data[mid]) {
tmpArr[third++] = data[left++];
} else {
tmpArr[third++] = data[mid++];
}
}
// 剩余部分依次放入临时数组(实际上两个 while 只会执行其中一个)
while (mid <= right) {
tmpArr[third++] = data[mid++];
}
while (left <= center) {
tmpArr[third++] = data[left++];
}
// 将临时数组中的内容拷贝回原数组中
// (原 left-right 范围的内容被复制回原数组)
while (tmp <= right) {
data[tmp] = tmpArr[tmp++];
}
}
public static void print(int[] data) {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + "\t");
}
System.out.println();
}
}
文章来源:https://blog.csdn.net/qq_24428851/article/details/135437245
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Hotspot源码解析-第十五章-类加载器初始化前期准备
- Spring高手之路-Spring事务的传播机制(行为、特性)
- 阿里云被拉入黑洞模式怎么办?该怎么换ip-速盾网络
- AutoSAR(基础入门篇)4.5-Autosar_BSW的Mode Management功能
- 告别低效!轻松创建在线文档,就用这6款协同办公神器!
- PyTorch官网demo解读——第一个神经网络(3)
- SAP不同语言开发
- 本地MinIO存储服务通过Java程序结合Cpolar内网穿透进行远程连接
- 分糖果C语言
- CentOS+shell脚本