力扣714. 买卖股票的最佳时机含手续费（java 动态规划）

Problem: 714. 买卖股票的最佳时机含手续费

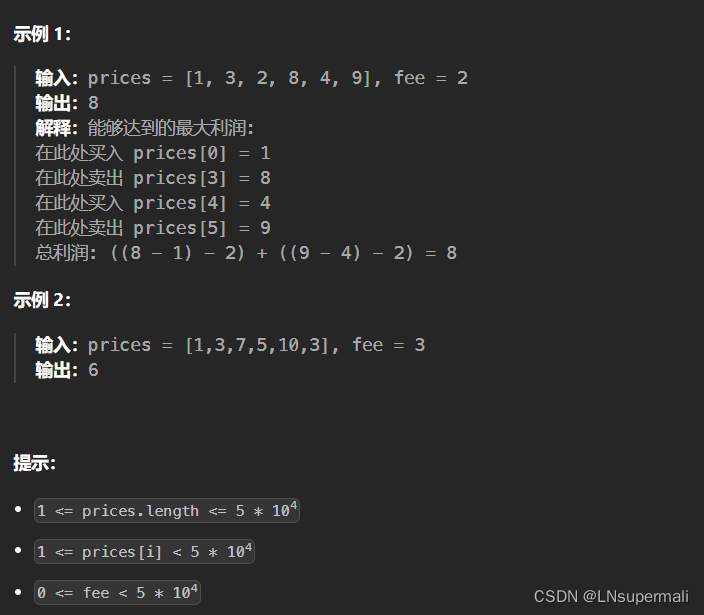
题目描述

思路

1.构建多阶段决策模型：n天对应n个阶段，每个阶段决策：买股票、卖股票、不操作；买股票只有当前不持有股票才行，卖股票只有当前持有股票才行，不操作无规则。
2.定义状态：每天有两种状态：持有股票、不持有股票。int dp[n][2]记录每个阶段的状态，dp[i][0]表示第i天持有股票可以获得的最大利润，dp[i][1]表示第i天不持有股票可以获得的最大利润。
3.定义状态转移方程：dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);即表示若当前持有股票则取出前一天持有股票的最大利润和不持有股票最大利润但减去当前的股票值二者中的最大值。其中dp[i - 1][1] - prices[i]就是表示：由于当前是持有股票，所有假设上一步不持有股票则当前的利润是要在上一步不持有股票最大利润的基础上减去当前购入股票（prices[i]）花费的价格,dp[i][1] = Math.max(dp[i][1], dp[i][0] + prices[i] - fee);即表示若当前不持有股票，则取出上一步不持有股票可以获得的最大利润和上一步持有股票再加上当前股票值（prices[i]）减去fee得到的利润二者中的最大值。其中dp[i][0] + prices[i] - fee是表示由于当前是不持有股票所以在上一步持有股票可以获得最大利润的基础上再去减去当前股票价格和交易费，则表示当前不再持有股票

解题方法

1.获取数组prices的长度n并申请一个int类型的二维数组（int[][] dp = new int[n][2]）其中dp[i][0]，与dp[i][1]表示的意义同上述思路；
2.初始化dp[0][0]为-prices[0]，表示最开始买入一个股票需要花费；dp[0][1]为0，表示最开始不持有股票可获得最大利润为0；
3.从第一个位置开始完成动态转移方程；
4.返回max(dp[n - 1][0], dp[n - 1][1]);

复杂度

时间复杂度:

$O(n)$其中$n$表示prices数组的大小

空间复杂度:

$O(n)$

Code

class Solution {
    /**
     * Dynamic programming
     *
     * @param prices The price of stock
     * @param fee    Handling charge
     * @return int
     */
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        //Recode the maximum profit
        int[][] dp = new int[n][2];
        //dp[i][0] represents the maximum profit
        // that can be made from holding the stock
        dp[0][0] = -prices[0];
        //dp[i][1] represents the maximum profit
        // that can be made by not holding the stock
        dp[0][1] = 0;
        for (int i = 1; i < n; ++i) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return Math.max(dp[n - 1][0], dp[n - 1][1]);
    }
}