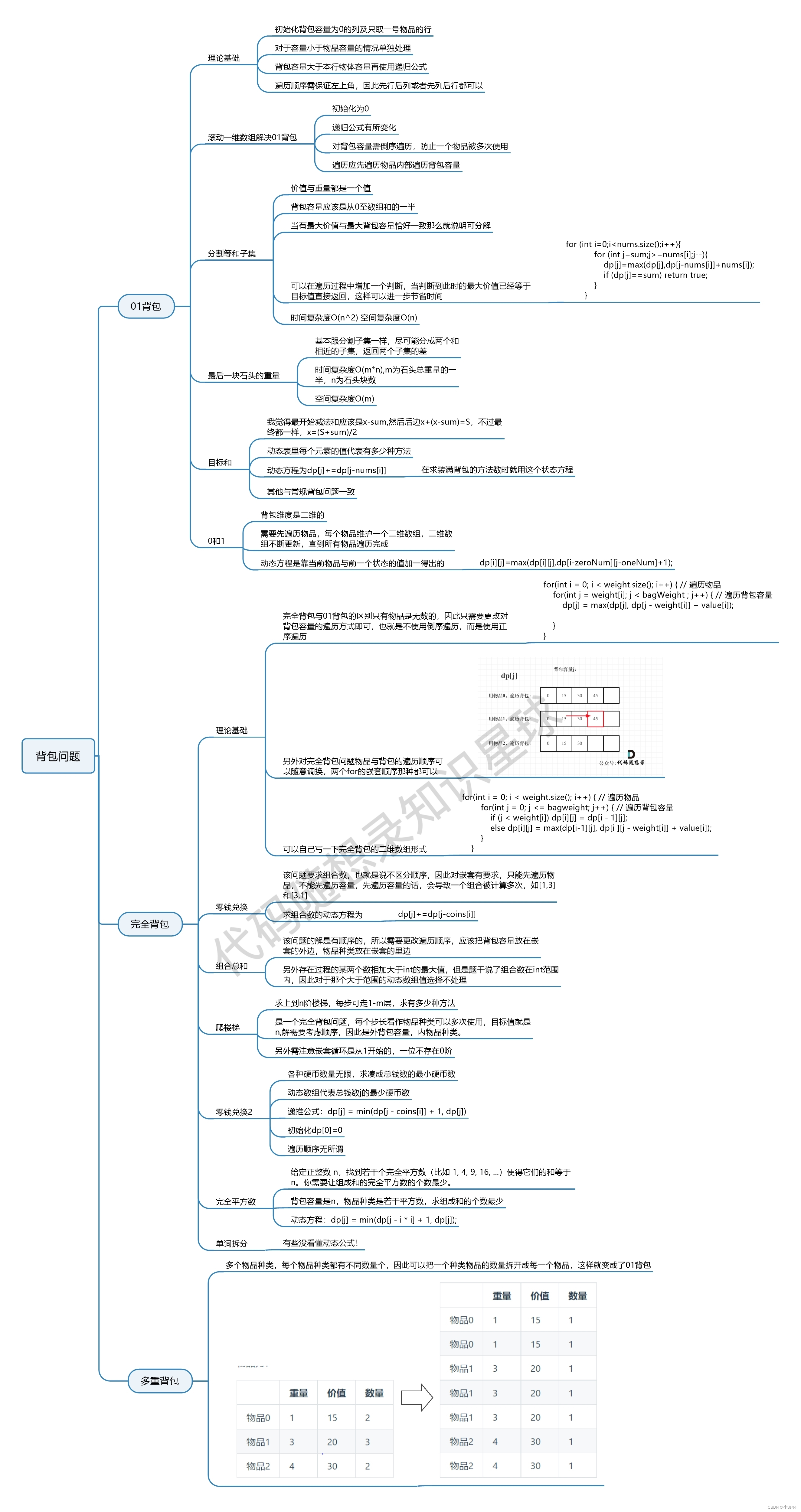
【代码随想录】刷题笔记Day46

前言

• 刚考完自辩，Chat回答举例什么的真方便。早上做组会PPT去了，火速来刷题！

139. 单词拆分 - 力扣（LeetCode）

• 单词是物品，字符串s是背包，单词能否组成字符串s，就是问物品能不能把背包装满
• 能重复用，是完全背包，其实也就是双指针的思想，i从头到尾，j从0到i
• dp[i]含义
  • 从头开始字符串长度为i，dp[i]为true表示可以拆分为在字典中出现的单词
• 递推公式
  • if( [j, i] 这个区间的子串出现在字典里 && dp[j]==true)? dp[i] = true
• 初始化
  • dp[0] = true， 其他为false
• 遍历顺序
  • 讲究顺序，用完全背包排列数的顺序，先背包后物品（双指针）
• 

• class Solution {
  public:
      bool wordBreak(string s, vector<string>& wordDict) {
          unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
          vector<bool> dp(s.size() + 1, false);
          dp[0] = true;
          for (int i = 1; i <= s.size(); i++) {   // 遍历背包
              for (int j = 0; j < i; j++) {       // 遍历物品(其实是子串的开始下标)
                  string word = s.substr(j, i - j); //substr(起始位置，截取的个数)
                  if (wordSet.find(word) != wordSet.end() && dp[j]) {
                      dp[i] = true;
                  }
              }
          }
          return dp[s.size()];
      }
  };

多重背包理论基础

• ?多重背包指的是有限个物品，其实把每个物品独立化后就是01背包问题了
• 
• 

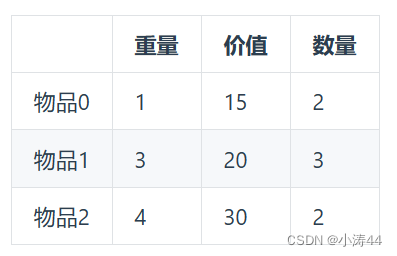
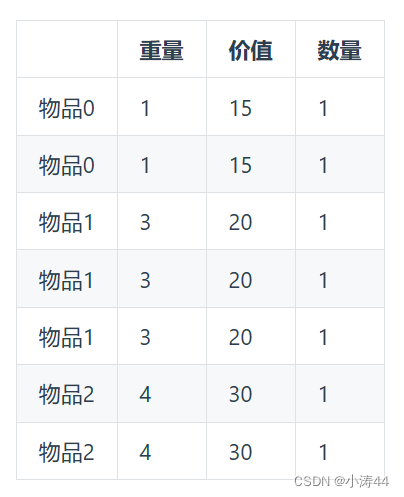
• for(int i = 0; i < n; i++) { // 遍历物品
      for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
          // 以上为01背包，然后加一个遍历个数
          for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
              dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
          }
      }
  }

?背包问题总结

?后言

• 背包问题终于结束啦，感觉这几道顺下来还是有点眉目的，只要把思路理清楚其实代码啪啪啪就可以打出来了（主要是因为比较简短，要考虑的特殊情况不多），今天是周五！下班！！