算法设计与分析 | 矩阵连乘

题目描述

??一个n*m矩阵由n行m列共n*m个数排列而成。两个矩阵A和B可以相乘当且仅当A的列数等于B的行数。一个N*M的矩阵乘以一个M*P的矩阵等于一个N*P的矩阵，运算量为nmp。
? 矩阵乘法满足结合律，A*B*C可以表示成(A*B)*C或者是A*(B*C)，两者的运算量却不同。例如当A=2*3 B=3*4 C=4*5时，(A*B)*C=64而A*(B*C)=90。显然第一种顺序节省运算量。
? 现在给出N个矩阵，并输入N+1个数，第i个矩阵是a[i-1]*a[i]

输入

第一行n(n<=100)
第二行n+1个数

输出

??最优的运算量

样例输入?

3
2 3 4 5

样例输出?

64

分析：

其实该题使用了动态规划来选出最优子结构，并且使用了以下等式：

先初始化m数组和s数组，这里使用了C++的函数memset():

void*?memset(void*?s,?int?c,?size_t?n);

参数解释：
-?`s`：指向要填充的内存区域的指针。
-?`c`：要设置的字符值（实际上是将其转换为对应的ASCII码或字节值）。
-?`n`：要填充的字节数。

`memset`函数将`s`指向的内存区域的前`n`个字节用`c`指定的值进行填充。返回值是原始的`s`指针。

并且m矩阵里面其实填充的是矩阵的右上角的部分，如可以看作下图这样：

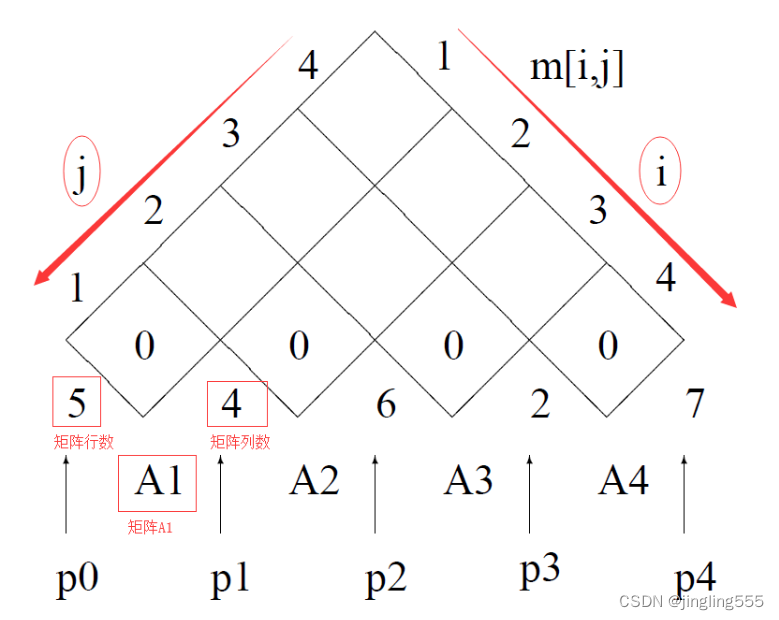
代码：

//矩阵连乘
#include<iostream>
#include<cstring> 
using namespace std;
const int size = 101;
int p[size];
int m[size][size], s[size][size];
int n;

void matrixchain()
{
	int i, r, j, k;
	memset(m, 0, sizeof(m));
	memset(s, 0, sizeof(s));//初始化数组
	for (r = 2; r <= n; r++)//矩阵连乘的规模为r 
	{
		for (i = 1; i <= n - r + 1; i++)
		{
			j = i + r - 1;
			m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];//对m[][]开始赋值
			s[i][j] = i;//s[][]存储各子问题的决策点
			for (k = i + 1; k < j; k++)//寻找最优值
			{
				int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
				if (t < m[i][j])
				{
					m[i][j] = t;
					s[i][j] = k;
				}
			}
		}
	}
}


int main()
{
	cin >> n;
	int i, j;
	for (i = 0; i <= n; i++)
		cin >> p[i];
	matrixchain();
	cout << m[1][n] << endl;

	return 0;
}

?参考博文：动态规划之——矩阵连乘（全网最详细博文，看这一篇就够了！）_矩阵连乘问题-CSDN博客