12.28数算编程专练

重构二叉树

序列重排

用嵌套容器解决，vector.back()返回此时容器的最后，尾端元素

struct node {
    int id;
    int next;
}n[100];
vector<vector<int>>t;
void add(int x) {
    if (t.empty()) {
        vector<int>n;
        n.push_back(x);
        t.push_back(n);
    }
    else {
        int i;
        for (i = 0; i < t.size(); i++) {
            if (x < t[i].back()) {
                t[i].push_back(x);
                break;//记得退出，不然会重复往t数组中加数据
            }
        }
        if (i == t.size()) {
            vector<int>n;
            n.push_back(x);
            t.push_back(n);
        }
    }
}
int n, temp;
cin >> n;
for (int i = 1; i <= n; i++) {
    cin >> temp;
    add(temp);
}
for (int i = 0; i < t.size(); i++) {
    if (t[i].back() == 1) {
        for (int j = 0; j < t[i].size(); j++)cout << t[i][j] << " ";
    }
    cout << endl;
    break;
}
cout << t.size();

后缀表达式求值

表达式求值

考虑算符优先级

建堆，两种建堆方式

欧拉回路

质数筛

将表达式用树表示

编程题的话，最短路、最小生成树、拓扑排序必定考一道

二分查找的细节

7-4 平均查找长度之线性再散列 分数 15

    int n, m, p;
    cin >> n >> m >> p;
    int arr[1000];
    int su = 0, fa = 0;
    for (int i = 0; i < m; i++)arr[i] = -1;
    for (int i = 1; i <= n; i++) {
        int num, cnt = 1;
        cin >> num;
        int index = num % p;
        while (arr[index] != -1) {
          //  cout << index << " ";
            cnt++;
            index = (index + 1) % m;
        }
       // cout << endl;
        arr[index] = num;
        su += cnt;
    }
    for (int i = 0; i < p; i++) {
        if (arr[i] == -1) { fa++; }
        else {
            int cnt = 1, j = i;
            while (arr[j]!=-1) {
                //cout << "fa" << i << " ";
                cnt++;
                j = (j + 1) % m;
            }
          //  cout << endl;
            fa += cnt;
        }
    }
    cout << su << "/" << n << endl;
    cout << fa << "/" << p << endl;

快排

如果基元是在最后的话，

第一个找比基元小的，就不需要设置一个i<j，小于右指针的限制，因为不会越界，最差就是i移动到基元的位置，所以循环一定会终止?

把奇数都放在偶数前

int oddb() {
    int c, i = 0, j = n - 1;
    while (i < j) {
        while (i < j && (a[i] % 2 == 1))i++;
        while (i < j && (a[i] % 2 == 0))j--;
        if (i < j) {
            int c = a[i];
            a[i] = a[j];
            a[j] = c;
            i++; j--;
        }
    }
}

二分查找（左闭右闭，循环条件记得加等号）

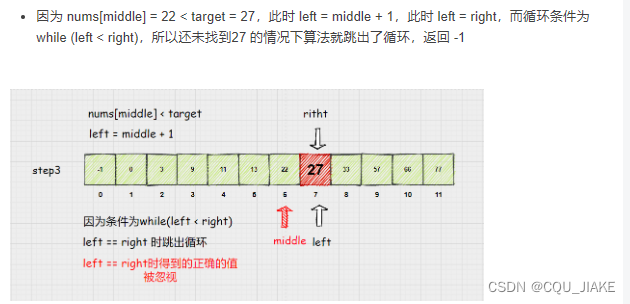
void searc() {//这是左闭右闭的二分查找
    int l, r;
    while (l <= r) {//这里注意，必须要加上=，必须要加上等于号，必要要加等于，不然就会在最后一次查询中，由于左右指针重合导致退出循环而不会返回
        int mid = (l + r) >> 1;
        if (a[mid] == t)return mid;
        else {
            if (a[mid] > t) {
                r = mid - 1;
            }
            else {
                l = mid + 1;
            }
        }
    }
}

归并排序