第 11 章树结构实际应用

发布时间：2024年01月14日

文章目录

11.1 堆排序
11.2 赫夫曼树
11.3 赫夫曼编码
11.4 二叉排序树
11.5 平衡二叉树(AVL 树)

11.1 堆排序

11.1.1 堆排序基本介绍

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为 O(nlogn)，它也是不稳定排序。
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。
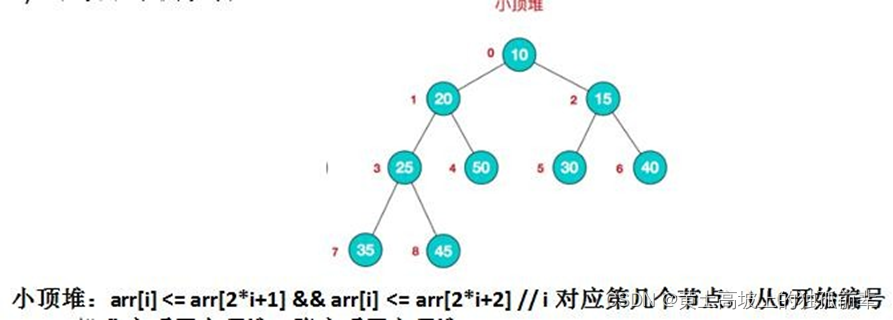
每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆
大顶堆举例说明
小顶堆举例说明
一般升序采用大顶堆，降序采用小顶堆

11.1.2 堆排序基本思想

堆排序的基本思想是：

将待排序序列构造成一个大顶堆
此时，整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换，此时末尾就为最大值。
然后将剩余 n-1 个元素重新构造成一个堆，这样会得到 n 个元素的次小值。如此反复执行，便能得到一个有序序列了。

可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列了.

11.1.3 堆排序步骤图解说明

要求：给你一个数组 {4,6,8,5,9} , 要求使用堆排序法，将数组升序排序。

步骤一
构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。原始的数组 [4, 6, 8, 5, 9]
1 .假设给定无序序列结构如下
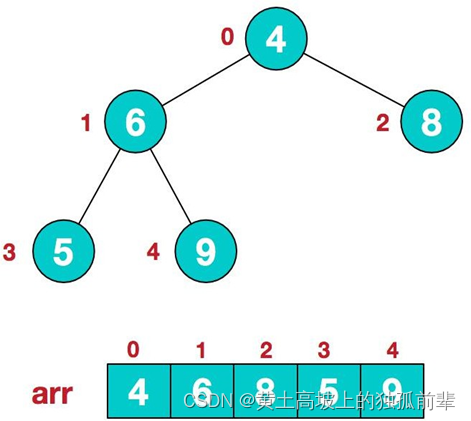在这里插入图片描述 2 .此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点
arr.length/2-1=5/2-1=1，也就是下面的 6 结点），从左至右，从下至上进行调整。

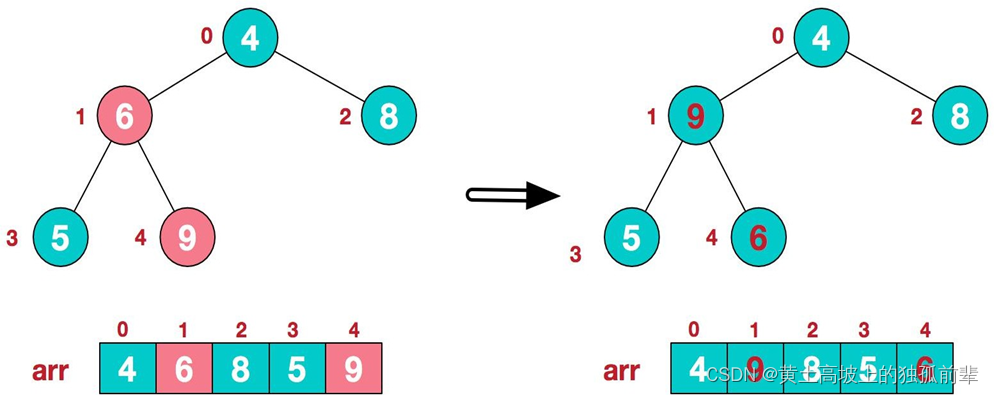
3.找到第二个非叶节点 4，由于[4,9,8]中 9 元素最大，4 和 9 交换。
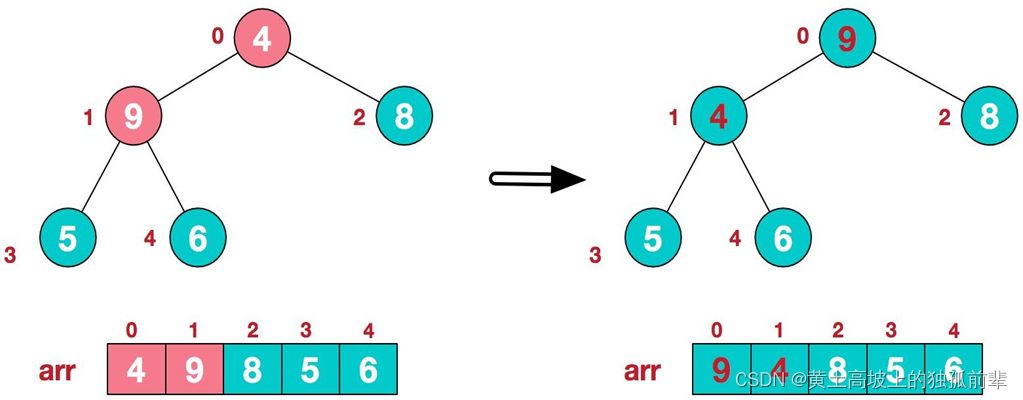
在这里插入图片描述
4.这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中 6 最大，交换 4 和 6。

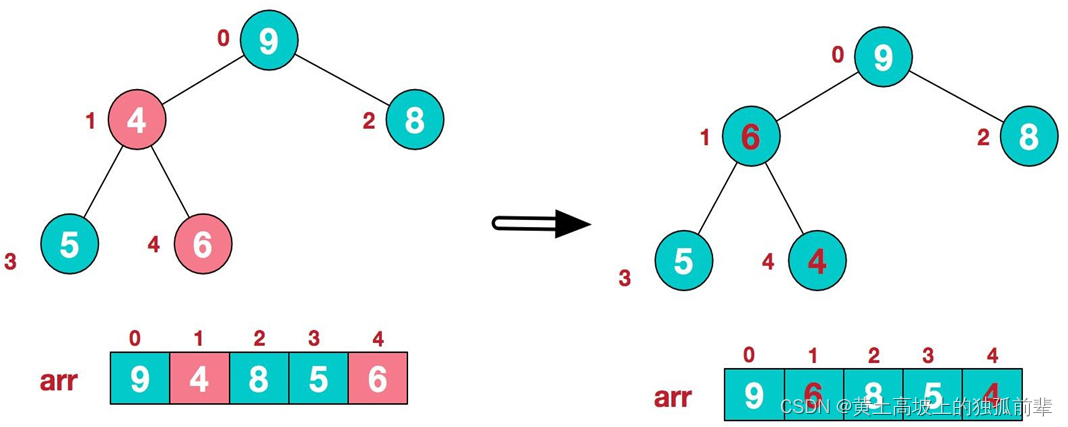在这里插入图片描述此时，我们就将一个无序序列构造成了一个大顶堆。

步骤二
将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，

得到第二大元素。如此反复进行交换、重建、交换。

1 .将堆顶元素 9 和末尾元素 4 进行交换
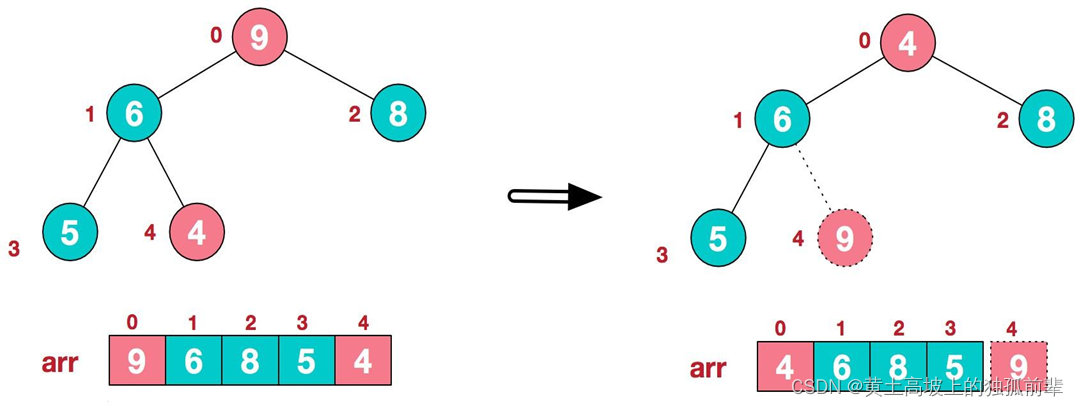
在这里插入图片描述
2 .重新调整结构，使其继续满足堆定义
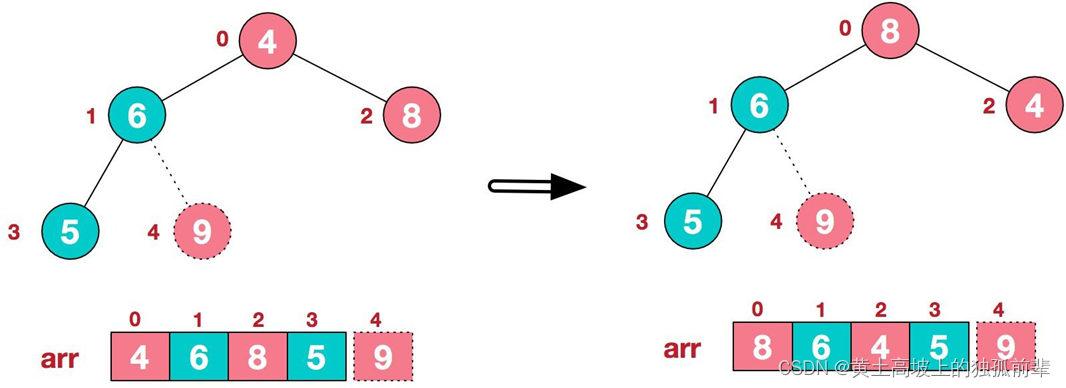3 .再将堆顶元素 8 与末尾元素 5 进行交换，得到第二大元素 8.

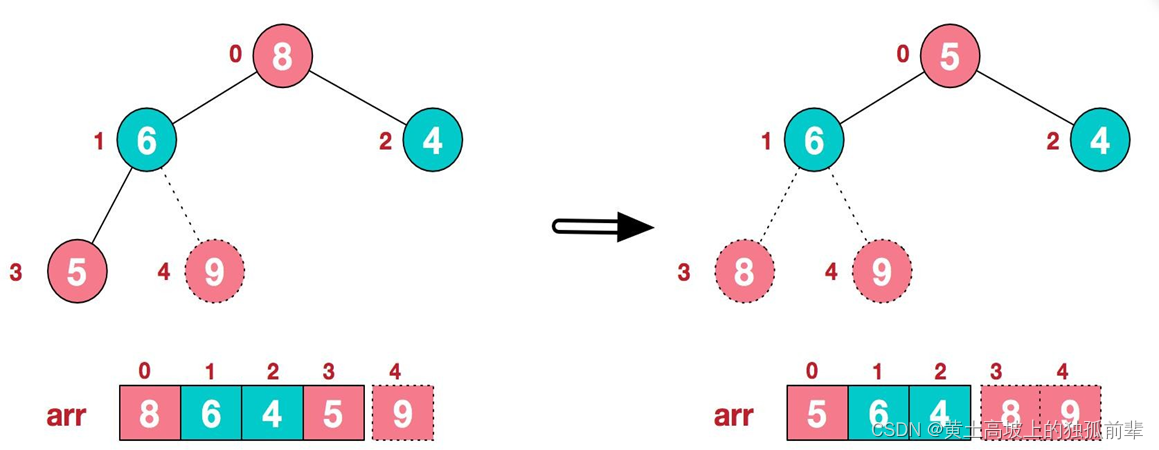
4.后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序
再简单总结下堆排序的基本思路：
1). 将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

2). 将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

3). 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

11.1.4 堆排序代码实现

要求：给你一个数组 {4,6,8,5,9} , 要求使用堆排序法，将数组升序排序。代码实现：看老师演示:
说明：

堆排序不是很好理解，老师通过 Debug 帮助大家理解堆排序
堆排序的速度非常快，在我的机器上 8 百万数据 3 秒左右。O(nlogn)

代码实现

 package com.atguigu.tree;

import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;

public class HeapSort {

	public static void main(String[] args) {
		//要求将数组进行升序排序
		//int arr[] = {4, 6, 8, 5, 9};
		// 创建要给80000个的随机的数组
		int[] arr = new int[8000000];
		for (int i = 0; i < 8000000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
		}

		System.out.println("排序前");
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("排序前的时间是=" + date1Str);
		
		heapSort(arr);
		
		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("排序前的时间是=" + date2Str);
		//System.out.println("排序后=" + Arrays.toString(arr));
	}

	//编写一个堆排序的方法
	public static void heapSort(int arr[]) {
		int temp = 0;
		System.out.println("堆排序!!");
		
//		//分步完成
//		adjustHeap(arr, 1, arr.length);
//		System.out.println("第一次" + Arrays.toString(arr)); // 4, 9, 8, 5, 6
//		
//		adjustHeap(arr, 0, arr.length);
//		System.out.println("第2次" + Arrays.toString(arr)); // 9,6,8,5,4
		
		//完成我们最终代码
		//将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆
		for(int i = arr.length / 2 -1; i >=0; i--) {
			adjustHeap(arr, i, arr.length);
		}
		
		/*
		 * 2).将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
　　			3).重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。
		 */
		for(int j = arr.length-1;j >0; j--) {
			//交换
			temp = arr[j];
			arr[j] = arr[0];
			arr[0] = temp;
			adjustHeap(arr, 0, j); 
		}
		
		//System.out.println("数组=" + Arrays.toString(arr)); 
		
	}
	
	//将一个数组(二叉树), 调整成一个大顶堆
	/**
	 * 功能： 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
	 * 举例  int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
	 * 如果我们再次调用  adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
	 * @param arr 待调整的数组
	 * @param i 表示非叶子结点在数组中索引
	 * @param lenght 表示对多少个元素继续调整， length 是在逐渐的减少
	 */
	public  static void adjustHeap(int arr[], int i, int lenght) {
		
		int temp = arr[i];//先取出当前元素的值，保存在临时变量
		//开始调整
		//说明
		//1. k = i * 2 + 1 k 是 i结点的左子结点
		for(int k = i * 2 + 1; k < lenght; k = k * 2 + 1) {
			if(k+1 < lenght && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
				k++; // k 指向右子结点
			}
			if(arr[k] > temp) { //如果子结点大于父结点
				arr[i] = arr[k]; //把较大的值赋给当前结点
				i = k; //!!! i 指向 k,继续循环比较
			} else {
				break;//!
			}
		}
		//当for 循环结束后，我们已经将以i 为父结点的树的最大值，放在了 最顶(局部)
		arr[i] = temp;//将temp值放到调整后的位置
	}
	
}

11.2 赫夫曼树

11.2.1 基本介绍

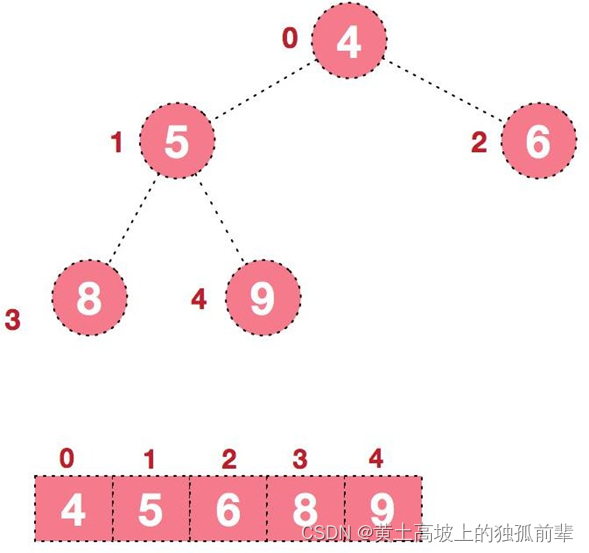
给定 n 个权值作为 n 个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。
赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近

11.2.2 赫夫曼树几个重要概念和举例说明

路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路

中分支的数目称为路径长度。若规定根结点的层数为 1，则从根结点到第 L 层结点的路径长度为 L-1
2) 结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积
3) 树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为 WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
4) WPL 最小的就是赫夫曼树
在这里插入图片描述

11.2.3 赫夫曼树创建思路图解

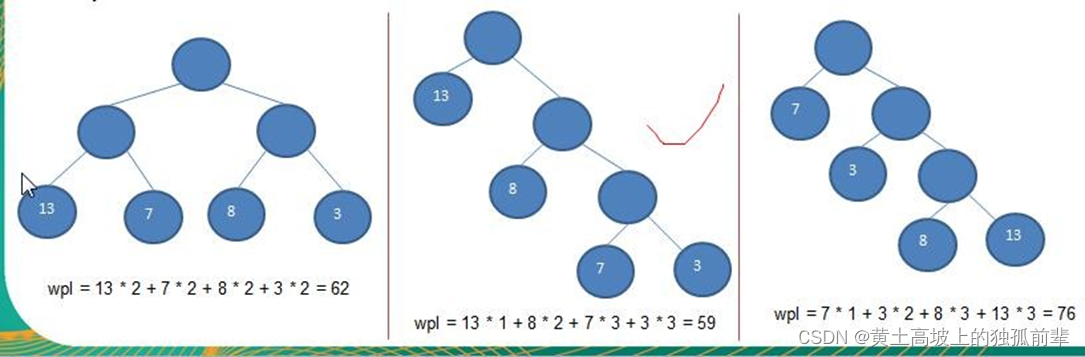
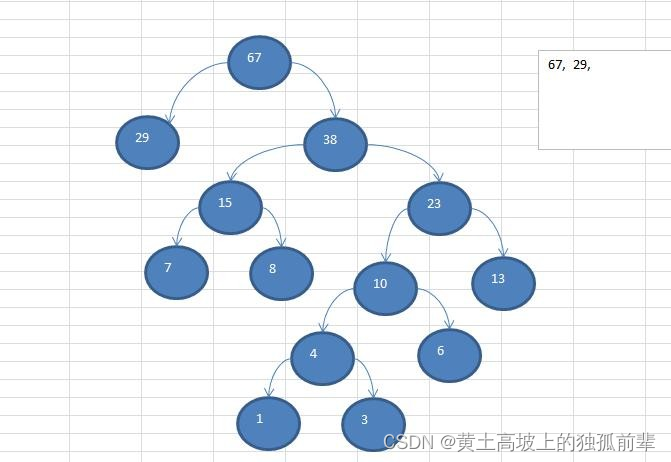
给你一个数列 {13, 7, 8, 3, 29, 6, 1}，要求转成一颗赫夫曼树.

? 思路分析(示意图)：
{13, 7, 8, 3, 29, 6, 1}

构成赫夫曼树的步骤：

从小到大进行排序, 将每一个数据，每个数据都是一个节点，每个节点可以看成是一颗最简单的二叉树
取出根节点权值最小的两颗二叉树
组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
再将这颗新的二叉树，以根节点的权值大小再次排序，不断重复 1-2-3-4 的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
图解:

11.2.4 赫夫曼树的代码实现

代码实现：

package com.atguigu.huffmantree;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class HuffmanTree {

	public static void main(String[] args) {
		int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
		Node root = createHuffmanTree(arr);
		
		//测试一把
		preOrder(root); //
		
	}
	
	//编写一个前序遍历的方法
	public static void preOrder(Node root) {
		if(root != null) {
			root.preOrder();
		}else{
			System.out.println("是空树，不能遍历~~");
		}
	}

	// 创建赫夫曼树的方法
	/**
	 * 
	 * @param arr 需要创建成哈夫曼树的数组
	 * @return 创建好后的赫夫曼树的root结点
	 */
	public static Node createHuffmanTree(int[] arr) {
		// 第一步为了操作方便
		// 1. 遍历 arr 数组
		// 2. 将arr的每个元素构成成一个Node
		// 3. 将Node 放入到ArrayList中
		List<Node> nodes = new ArrayList<Node>();
		for (int value : arr) {
			nodes.add(new Node(value));
		}
		
		//我们处理的过程是一个循环的过程
		
		
		while(nodes.size() > 1) {
		
			//排序 从小到大 
			Collections.sort(nodes);
			
			System.out.println("nodes =" + nodes);
			
			//取出根节点权值最小的两颗二叉树 
			//(1) 取出权值最小的结点（二叉树）
			Node leftNode = nodes.get(0);
			//(2) 取出权值第二小的结点（二叉树）
			Node rightNode = nodes.get(1);
			
			//(3)构建一颗新的二叉树
			Node parent = new Node(leftNode.value + rightNode.value);
			parent.left = leftNode;
			parent.right = rightNode;
			
			//(4)从ArrayList删除处理过的二叉树
			nodes.remove(leftNode);
			nodes.remove(rightNode);
			//(5)将parent加入到nodes
			nodes.add(parent);
		}
		
		//返回哈夫曼树的root结点
		return nodes.get(0);
		
	}
}

// 创建结点类
// 为了让Node 对象持续排序Collections集合排序
// 让Node 实现Comparable接口
class Node implements Comparable<Node> {
	int value; // 结点权值
	char c; //字符
	Node left; // 指向左子结点
	Node right; // 指向右子结点

	//写一个前序遍历
	public void preOrder() {
		System.out.println(this);
		if(this.left != null) {
			this.left.preOrder();
		}
		if(this.right != null) {
			this.right.preOrder();
		}
	}
	
	public Node(int value) {
		this.value = value;
	}

	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	@Override
	public int compareTo(Node o) {
		// TODO Auto-generated method stub
		// 表示从小到大排序
		return this.value - o.value;
	}

}

11.3 赫夫曼编码

11.3.1 基本介绍

赫夫曼编码也翻译为哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式, 属于一种程序算法
赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在 20%～90%之间
赫夫曼码是可变字长编码(VLC)的一种。Huffman 于 1952 年提出一种编码方法，称之为最佳编码

11.3.2 原理剖析

? 通信领域中信息的处理方式 1-定长编码
在这里插入图片描述

? 通信领域中信息的处理方式 2-变长编码
在这里插入图片描述

? 通信领域中信息的处理方式 3-赫夫曼编码
步骤如下;
输的字符串

i like like like java do you like a java
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数
按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值
步骤：
构成赫夫曼树的步骤：
1. 从小到大进行排序, 将每一个数据，每个数据都是一个节点，每个节点可以看成是一颗最简单的二叉树
2. 取出根节点权值最小的两颗二叉树
3. 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
4. 再将这颗新的二叉树，以根节点的权值大小再次排序，不断重复 1-2-3-4 的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树

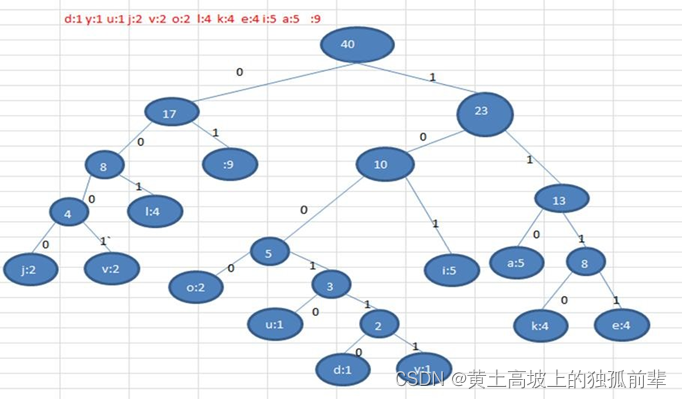
4.根据赫夫曼树，给各个字符,规定编码 (前缀编码)，向左的路径为 0 向右的路径为 1 ，编码如下:
o: 1000 u: 10010 d: 100110 y: 100111 i: 101

a : 110 k: 1110 e: 1111 j: 0000 v: 0001
l: 001 01

5.按照上面的赫夫曼编码，我们的"i like like like java do you like a java" 字符串对应的编码为 (注意这里我们使用的无损压缩) 10101001101111011110100110111101111010011011110111101000011000011100110011110000110
01111000100100100110111101111011100100001100001110 通过赫夫曼编码处理长度为 133

6 . 长度为： 133
说明:
原来长度是 359 , 压缩了 (359-133) / 359 = 62.9%

? 注意事项
注意, 这个赫夫曼树根据排序方法不同，也可能不太一样，这样对应的赫夫曼编码也不完全一样，但是 wpl 是一样的，都是最小的, 最后生成的赫夫曼编码的长度是一样，比如: 如果我们让每次生成的新的二叉树总是排在权值相同的二叉树的最后一个，则生成的二叉树为:
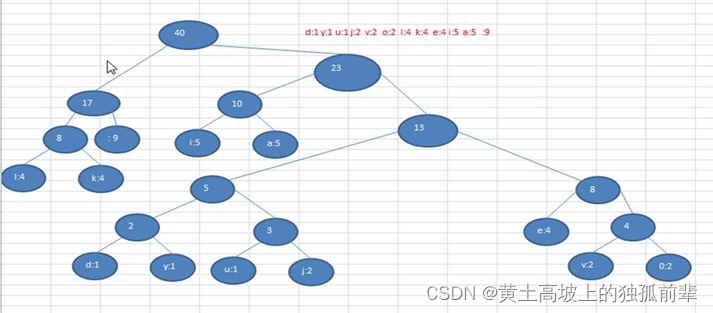
在这里插入图片描述

11.3.3 最佳实践-数据压缩(创建赫夫曼树)

将给出的一段文本，比如 “i like like like java do you like a java” ，根据前面的讲的赫夫曼编码原理，对其进行数据压缩处理，形式如 "1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100
110111101111011100100001100001110 "

步骤 1：根据赫夫曼编码压缩数据的原理，需要创建 “i like like like java do you like a java” 对应的赫夫曼树.

思路：前面已经分析过了，而且我们已然讲过了构建赫夫曼树的具体实现。代码实现：

//可以通过List 创建对应的赫夫曼树
	private static Node createHuffmanTree(List<Node> nodes) {
		
		while(nodes.size() > 1) {
			//排序, 从小到大
			Collections.sort(nodes);
			//取出第一颗最小的二叉树
			Node leftNode = nodes.get(0);
			//取出第二颗最小的二叉树
			Node rightNode = nodes.get(1);
			//创建一颗新的二叉树,它的根节点 没有data, 只有权值
			Node parent = new Node(null, leftNode.weight + rightNode.weight);
			parent.left = leftNode;
			parent.right = rightNode;
			
			//将已经处理的两颗二叉树从nodes删除
			nodes.remove(leftNode);
			nodes.remove(rightNode);
			//将新的二叉树，加入到nodes
			nodes.add(parent);
			
		}
		//nodes 最后的结点，就是赫夫曼树的根结点
		return nodes.get(0);
		
	}

11.3.4 最佳实践-数据压缩(生成赫夫曼编码和赫夫曼编码后的数据)

我们已经生成了赫夫曼树, 下面我们继续完成任务

生成赫夫曼树对应的赫夫曼编码 , 如下表:
=01 a=100 d=11000 u=11001 e=1110 v=11011 i=101 y=11010 j=0010 k=1111 l=000 o=0011
使用赫夫曼编码来生成赫夫曼编码数据 ,即按照上面的赫夫曼编码，将"i like like like java do you like a java"字符串生成对应的编码数据, 形式如下. 10101000101111111100100010111111110010001011111111001001010011011100011100000110111010001111001010
00101111111100110001001010011011100
思路：前面已经分析过了，而且我们讲过了生成赫夫曼编码的具体实现。

代码实现：

 /**
	 * 功能：将传入的node结点的所有叶子结点的赫夫曼编码得到，并放入到huffmanCodes集合
	 * @param node  传入结点
	 * @param code  路径： 左子结点是 0, 右子结点 1
	 * @param stringBuilder 用于拼接路径
	 */
	private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
		StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
		//将code 加入到 stringBuilder2
		stringBuilder2.append(code);
		if(node != null) { //如果node == null不处理
			//判断当前node 是叶子结点还是非叶子结点
			if(node.data == null) { //非叶子结点
				//递归处理
				//向左递归
				getCodes(node.left, "0", stringBuilder2);
				//向右递归
				getCodes(node.right, "1", stringBuilder2);
			} else { //说明是一个叶子结点
				//就表示找到某个叶子结点的最后
				huffmanCodes.put(node.data, stringBuilder2.toString());
			}
		}
	}

11.3.5 最佳实践-数据解压(使用赫夫曼编码解码)

使用赫夫曼编码来解码数据，具体要求是

前面我们得到了赫夫曼编码和对应的编码
byte[] , 即:[-88, -65, -56, -65, -56, -65, -55, 77
, -57, 6, -24, -14, -117, -4, -60, -90, 28]
现在要求使用赫夫曼编码，进行解码，又
重新得到原来的字符串"i like like like java do you like a java"
思路：解码过程，就是编码的一个逆向操作。

代码实现：

 /**
	 * 将一个byte 转成一个二进制的字符串, 如果看不懂，可以参考我讲的Java基础 二进制的原码，反码，补码
	 * @param b 传入的 byte
	 * @param flag 标志是否需要补高位如果是true ，表示需要补高位，如果是false表示不补, 如果是最后一个字节，无需补高位
	 * @return 是该b 对应的二进制的字符串，（注意是按补码返回）
	 */
	private static String byteToBitString(boolean flag, byte b) {
		//使用变量保存 b
		int temp = b; //将 b 转成 int
		//如果是正数我们还存在补高位
		if(flag) {
			temp |= 256; //按位与 256  1 0000 0000  | 0000 0001 => 1 0000 0001
		}
		String str = Integer.toBinaryString(temp); //返回的是temp对应的二进制的补码
		if(flag) {
			return str.substring(str.length() - 8);
		} else {
			return str;
		}
	}


//编写一个方法，完成对压缩数据的解码
	/**
	 * 
	 * @param huffmanCodes 赫夫曼编码表 map
	 * @param huffmanBytes 赫夫曼编码得到的字节数组
	 * @return 就是原来的字符串对应的数组
	 */
	private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
		
		//1. 先得到 huffmanBytes 对应的 二进制的字符串 ， 形式 1010100010111...
		StringBuilder stringBuilder = new StringBuilder();
		//将byte数组转成二进制的字符串
		for(int i = 0; i < huffmanBytes.length; i++) {
			byte b = huffmanBytes[i];
			//判断是不是最后一个字节
			boolean flag = (i == huffmanBytes.length - 1);
			stringBuilder.append(byteToBitString(!flag, b));
		}
		//把字符串安装指定的赫夫曼编码进行解码
		//把赫夫曼编码表进行调换，因为反向查询 a->100 100->a
		Map<String, Byte>  map = new HashMap<String,Byte>();
		for(Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
			map.put(entry.getValue(), entry.getKey());
		}
		
		//创建要给集合，存放byte
		List<Byte> list = new ArrayList<>();
		//i 可以理解成就是索引,扫描 stringBuilder 
		for(int  i = 0; i < stringBuilder.length(); ) {
			int count = 1; // 小的计数器
			boolean flag = true;
			Byte b = null;
			
			while(flag) {
				//1010100010111...
				//递增的取出 key 1 
				String key = stringBuilder.substring(i, i+count);//i 不动，让count移动，指定匹配到一个字符
				b = map.get(key);
				if(b == null) {//说明没有匹配到
					count++;
				}else {
					//匹配到
					flag = false;
				}
			}
			list.add(b);
			i += count;//i 直接移动到 count	
		}
		//当for循环结束后，我们list中就存放了所有的字符  "i like like like java do you like a java"
		//把list 中的数据放入到byte[] 并返回
		byte b[] = new byte[list.size()];
		for(int i = 0;i < b.length; i++) {
			b[i] = list.get(i);
		}
		return b;
		
	}

11.3.6 最佳实践-文件压缩

我们学习了通过赫夫曼编码对一个字符串进行编码和解码, 下面我们来完成对文件的压缩和解压，具体要求：给你一个图片文件，要求对其进行无损压缩, 看看压缩效果如何。

思路：读取文件-> 得到赫夫曼编码表 -> 完成压缩

代码实现：

 //编写一个方法，完成对压缩文件的解压
	/**
	 * 
	 * @param zipFile 准备解压的文件
	 * @param dstFile 将文件解压到哪个路径
	 */
	public static void unZipFile(String zipFile, String dstFile) {
		
		//定义文件输入流
		InputStream is = null;
		//定义一个对象输入流
		ObjectInputStream ois = null;
		//定义文件的输出流
		OutputStream os = null;
		try {
			//创建文件输入流
			is = new FileInputStream(zipFile);
			//创建一个和  is关联的对象输入流
			ois = new ObjectInputStream(is);
			//读取byte数组  huffmanBytes
			byte[] huffmanBytes = (byte[])ois.readObject();
			//读取赫夫曼编码表
			Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
			
			//解码
			byte[] bytes = decode(huffmanCodes, huffmanBytes);
			//将bytes 数组写入到目标文件
			os = new FileOutputStream(dstFile);
			//写数据到 dstFile 文件
			os.write(bytes);
		} catch (Exception e) {
			// TODO: handle exception
			System.out.println(e.getMessage());
		} finally {
			
			try {
				os.close();
				ois.close();
				is.close();
			} catch (Exception e2) {
				// TODO: handle exception
				System.out.println(e2.getMessage());
			}
			
		}
	}

11.3.7 最佳实践-文件解压(文件恢复)

具体要求：将前面压缩的文件，重新恢复成原来的文件。

思路：读取压缩文件(数据和赫夫曼编码表)-> 完成解压(文件恢复)

代码实现：

 //编写一个方法，完成对压缩文件的解压
	/**
	 * 
	 * @param zipFile 准备解压的文件
	 * @param dstFile 将文件解压到哪个路径
	 */
	public static void unZipFile(String zipFile, String dstFile) {
		
		//定义文件输入流
		InputStream is = null;
		//定义一个对象输入流
		ObjectInputStream ois = null;
		//定义文件的输出流
		OutputStream os = null;
		try {
			//创建文件输入流
			is = new FileInputStream(zipFile);
			//创建一个和  is关联的对象输入流
			ois = new ObjectInputStream(is);
			//读取byte数组  huffmanBytes
			byte[] huffmanBytes = (byte[])ois.readObject();
			//读取赫夫曼编码表
			Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
			
			//解码
			byte[] bytes = decode(huffmanCodes, huffmanBytes);
			//将bytes 数组写入到目标文件
			os = new FileOutputStream(dstFile);
			//写数据到 dstFile 文件
			os.write(bytes);
		} catch (Exception e) {
			// TODO: handle exception
			System.out.println(e.getMessage());
		} finally {
			
			try {
				os.close();
				ois.close();
				is.close();
			} catch (Exception e2) {
				// TODO: handle exception
				System.out.println(e2.getMessage());
			}
			
		}
	}

11.3.8 代码汇总，把前面所有的方法放在一起

	package com.atguigu.huffmancode;
	
	import java.io.FileInputStream;
	import java.io.FileOutputStream;
	import java.io.InputStream;
	import java.io.ObjectInputStream;
	import java.io.ObjectOutputStream;
	import java.io.OutputStream;
	import java.util.ArrayList;
	import java.util.Arrays;
	import java.util.Collections;
	import java.util.HashMap;
	import java.util.List;
	import java.util.Map;
	
	public class HuffmanCode {
	
		public static void main(String[] args) {
			
			//测试压缩文件
	//		String srcFile = "d://Uninstall.xml";
	//		String dstFile = "d://Uninstall.zip";
	//		
	//		zipFile(srcFile, dstFile);
	//		System.out.println("压缩文件ok~~");
			
			
			//测试解压文件
			String zipFile = "d://Uninstall.zip";
			String dstFile = "d://Uninstall2.xml";
			unZipFile(zipFile, dstFile);
			System.out.println("解压成功!");
			
			/*
			String content = "i like like like java do you like a java";
			byte[] contentBytes = content.getBytes();
			System.out.println(contentBytes.length); //40
			
			byte[] huffmanCodesBytes= huffmanZip(contentBytes);
			System.out.println("压缩后的结果是:" + Arrays.toString(huffmanCodesBytes) + " 长度= " + huffmanCodesBytes.length);
			
			
			//测试一把byteToBitString方法
			//System.out.println(byteToBitString((byte)1));
			byte[] sourceBytes = decode(huffmanCodes, huffmanCodesBytes);
			
			System.out.println("原来的字符串=" + new String(sourceBytes)); // "i like like like java do you like a java"
			*/
			
			
			
			//如何将 数据进行解压(解码)  
			//分步过程
			/*
			List<Node> nodes = getNodes(contentBytes);
			System.out.println("nodes=" + nodes);
			
			//测试一把，创建的赫夫曼树
			System.out.println("赫夫曼树");
			Node huffmanTreeRoot = createHuffmanTree(nodes);
			System.out.println("前序遍历");
			huffmanTreeRoot.preOrder();
			
			//测试一把是否生成了对应的赫夫曼编码
			Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
			System.out.println("~生成的赫夫曼编码表= " + huffmanCodes);
			
			//测试
			byte[] huffmanCodeBytes = zip(contentBytes, huffmanCodes);
			System.out.println("huffmanCodeBytes=" + Arrays.toString(huffmanCodeBytes));//17
			
			//发送huffmanCodeBytes 数组 */
			
			
		}
		
		//编写一个方法，完成对压缩文件的解压
		/**
		 * 
		 * @param zipFile 准备解压的文件
		 * @param dstFile 将文件解压到哪个路径
		 */
		public static void unZipFile(String zipFile, String dstFile) {
			
			//定义文件输入流
			InputStream is = null;
			//定义一个对象输入流
			ObjectInputStream ois = null;
			//定义文件的输出流
			OutputStream os = null;
			try {
				//创建文件输入流
				is = new FileInputStream(zipFile);
				//创建一个和  is关联的对象输入流
				ois = new ObjectInputStream(is);
				//读取byte数组  huffmanBytes
				byte[] huffmanBytes = (byte[])ois.readObject();
				//读取赫夫曼编码表
				Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
				
				//解码
				byte[] bytes = decode(huffmanCodes, huffmanBytes);
				//将bytes 数组写入到目标文件
				os = new FileOutputStream(dstFile);
				//写数据到 dstFile 文件
				os.write(bytes);
			} catch (Exception e) {
				// TODO: handle exception
				System.out.println(e.getMessage());
			} finally {
				
				try {
					os.close();
					ois.close();
					is.close();
				} catch (Exception e2) {
					// TODO: handle exception
					System.out.println(e2.getMessage());
				}
				
			}
		}
		
		//编写方法，将一个文件进行压缩
		/**
		 * 
		 * @param srcFile 你传入的希望压缩的文件的全路径
		 * @param dstFile 我们压缩后将压缩文件放到哪个目录
		 */
		public static void zipFile(String srcFile, String dstFile) {
			
			//创建输出流
			OutputStream os = null;
			ObjectOutputStream oos = null;
			//创建文件的输入流
			FileInputStream is = null;
			try {
				//创建文件的输入流
				is = new FileInputStream(srcFile);
				//创建一个和源文件大小一样的byte[]
				byte[] b = new byte[is.available()];
				//读取文件
				is.read(b);
				//直接对源文件压缩
				byte[] huffmanBytes = huffmanZip(b);
				//创建文件的输出流, 存放压缩文件
				os = new FileOutputStream(dstFile);
				//创建一个和文件输出流关联的ObjectOutputStream
				oos = new ObjectOutputStream(os);
				//把 赫夫曼编码后的字节数组写入压缩文件
				oos.writeObject(huffmanBytes); //我们是把
				//这里我们以对象流的方式写入 赫夫曼编码，是为了以后我们恢复源文件时使用
				//注意一定要把赫夫曼编码 写入压缩文件
				oos.writeObject(huffmanCodes);
				
				
			}catch (Exception e) {
				// TODO: handle exception
				System.out.println(e.getMessage());
			}finally {
				try {
					is.close();
					oos.close();
					os.close();
				}catch (Exception e) {
					// TODO: handle exception
					System.out.println(e.getMessage());
				}
			}
			
		}
		
		//完成数据的解压
		//思路
		//1. 将huffmanCodeBytes [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
		//   重写先转成 赫夫曼编码对应的二进制的字符串 "1010100010111..."
		//2.  赫夫曼编码对应的二进制的字符串 "1010100010111..." =》 对照 赫夫曼编码  =》 "i like like like java do you like a java"
		
		
		//编写一个方法，完成对压缩数据的解码
		/**
		 * 
		 * @param huffmanCodes 赫夫曼编码表 map
		 * @param huffmanBytes 赫夫曼编码得到的字节数组
		 * @return 就是原来的字符串对应的数组
		 */
		private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
			
			//1. 先得到 huffmanBytes 对应的 二进制的字符串 ， 形式 1010100010111...
			StringBuilder stringBuilder = new StringBuilder();
			//将byte数组转成二进制的字符串
			for(int i = 0; i < huffmanBytes.length; i++) {
				byte b = huffmanBytes[i];
				//判断是不是最后一个字节
				boolean flag = (i == huffmanBytes.length - 1);
				stringBuilder.append(byteToBitString(!flag, b));
			}
			//把字符串安装指定的赫夫曼编码进行解码
			//把赫夫曼编码表进行调换，因为反向查询 a->100 100->a
			Map<String, Byte>  map = new HashMap<String,Byte>();
			for(Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
				map.put(entry.getValue(), entry.getKey());
			}
			
			//创建要给集合，存放byte
			List<Byte> list = new ArrayList<>();
			//i 可以理解成就是索引,扫描 stringBuilder 
			for(int  i = 0; i < stringBuilder.length(); ) {
				int count = 1; // 小的计数器
				boolean flag = true;
				Byte b = null;
				
				while(flag) {
					//1010100010111...
					//递增的取出 key 1 
					String key = stringBuilder.substring(i, i+count);//i 不动，让count移动，指定匹配到一个字符
					b = map.get(key);
					if(b == null) {//说明没有匹配到
						count++;
					}else {
						//匹配到
						flag = false;
					}
				}
				list.add(b);
				i += count;//i 直接移动到 count	
			}
			//当for循环结束后，我们list中就存放了所有的字符  "i like like like java do you like a java"
			//把list 中的数据放入到byte[] 并返回
			byte b[] = new byte[list.size()];
			for(int i = 0;i < b.length; i++) {
				b[i] = list.get(i);
			}
			return b;
			
		}
	 	
		/**
		 * 将一个byte 转成一个二进制的字符串, 如果看不懂，可以参考我讲的Java基础 二进制的原码，反码，补码
		 * @param b 传入的 byte
		 * @param flag 标志是否需要补高位如果是true ，表示需要补高位，如果是false表示不补, 如果是最后一个字节，无需补高位
		 * @return 是该b 对应的二进制的字符串，（注意是按补码返回）
		 */
		private static String byteToBitString(boolean flag, byte b) {
			//使用变量保存 b
			int temp = b; //将 b 转成 int
			//如果是正数我们还存在补高位
			if(flag) {
				temp |= 256; //按位与 256  1 0000 0000  | 0000 0001 => 1 0000 0001
			}
			String str = Integer.toBinaryString(temp); //返回的是temp对应的二进制的补码
			if(flag) {
				return str.substring(str.length() - 8);
			} else {
				return str;
			}
		}
		
		//使用一个方法，将前面的方法封装起来，便于我们的调用.
		/**
		 * 
		 * @param bytes 原始的字符串对应的字节数组
		 * @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
		 */
		private static byte[] huffmanZip(byte[] bytes) {
			List<Node> nodes = getNodes(bytes);
			//根据 nodes 创建的赫夫曼树
			Node huffmanTreeRoot = createHuffmanTree(nodes);
			//对应的赫夫曼编码(根据 赫夫曼树)
			Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
			//根据生成的赫夫曼编码，压缩得到压缩后的赫夫曼编码字节数组
			byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
			return huffmanCodeBytes;
		}
		
		
		//编写一个方法，将字符串对应的byte[] 数组，通过生成的赫夫曼编码表，返回一个赫夫曼编码 压缩后的byte[]
		/**
		 * 
		 * @param bytes 这时原始的字符串对应的 byte[]
		 * @param huffmanCodes 生成的赫夫曼编码map
		 * @return 返回赫夫曼编码处理后的 byte[] 
		 * 举例： String content = "i like like like java do you like a java"; =》 byte[] contentBytes = content.getBytes();
		 * 返回的是 字符串 "1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100"
		 * => 对应的 byte[] huffmanCodeBytes  ，即 8位对应一个 byte,放入到 huffmanCodeBytes
		 * huffmanCodeBytes[0] =  10101000(补码) => byte  [推导  10101000=> 10101000 - 1 => 10100111(反码)=> 11011000= -88 ]
		 * huffmanCodeBytes[1] = -88
		 */
		private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
			
			//1.利用 huffmanCodes 将  bytes 转成  赫夫曼编码对应的字符串
			StringBuilder stringBuilder = new StringBuilder();
			//遍历bytes 数组 
			for(byte b: bytes) {
				stringBuilder.append(huffmanCodes.get(b));
			}
			
			//System.out.println("测试 stringBuilder~~~=" + stringBuilder.toString());
			
			//将 "1010100010111111110..." 转成 byte[]
			
			//统计返回  byte[] huffmanCodeBytes 长度
			//一句话 int len = (stringBuilder.length() + 7) / 8;
			int len;
			if(stringBuilder.length() % 8 == 0) {
				len = stringBuilder.length() / 8;
			} else {
				len = stringBuilder.length() / 8 + 1;
			}
			//创建 存储压缩后的 byte数组
			byte[] huffmanCodeBytes = new byte[len];
			int index = 0;//记录是第几个byte
			for (int i = 0; i < stringBuilder.length(); i += 8) { //因为是每8位对应一个byte,所以步长 +8
					String strByte;
					if(i+8 > stringBuilder.length()) {//不够8位
						strByte = stringBuilder.substring(i);
					}else{
						strByte = stringBuilder.substring(i, i + 8);
					}	
					//将strByte 转成一个byte,放入到 huffmanCodeBytes
					huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
					index++;
			}
			return huffmanCodeBytes;
		}
		
		//生成赫夫曼树对应的赫夫曼编码
		//思路:
		//1. 将赫夫曼编码表存放在 Map<Byte,String> 形式
		//   生成的赫夫曼编码表{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
		static Map<Byte, String> huffmanCodes = new HashMap<Byte,String>();
		//2. 在生成赫夫曼编码表示，需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
		static StringBuilder stringBuilder = new StringBuilder();
		
		
		//为了调用方便，我们重载 getCodes
		private static Map<Byte, String> getCodes(Node root) {
			if(root == null) {
				return null;
			}
			//处理root的左子树
			getCodes(root.left, "0", stringBuilder);
			//处理root的右子树
			getCodes(root.right, "1", stringBuilder);
			return huffmanCodes;
		}
		
		/**
		 * 功能：将传入的node结点的所有叶子结点的赫夫曼编码得到，并放入到huffmanCodes集合
		 * @param node  传入结点
		 * @param code  路径： 左子结点是 0, 右子结点 1
		 * @param stringBuilder 用于拼接路径
		 */
		private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
			StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
			//将code 加入到 stringBuilder2
			stringBuilder2.append(code);
			if(node != null) { //如果node == null不处理
				//判断当前node 是叶子结点还是非叶子结点
				if(node.data == null) { //非叶子结点
					//递归处理
					//向左递归
					getCodes(node.left, "0", stringBuilder2);
					//向右递归
					getCodes(node.right, "1", stringBuilder2);
				} else { //说明是一个叶子结点
					//就表示找到某个叶子结点的最后
					huffmanCodes.put(node.data, stringBuilder2.toString());
				}
			}
		}
		
		//前序遍历的方法
		private static void preOrder(Node root) {
			if(root != null) {
				root.preOrder();
			}else {
				System.out.println("赫夫曼树为空");
			}
		}
		
		/**
		 * 
		 * @param bytes 接收字节数组
		 * @return 返回的就是 List 形式   [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
		 */
		private static List<Node> getNodes(byte[] bytes) {
			
			//1创建一个ArrayList
			ArrayList<Node> nodes = new ArrayList<Node>();
			
			//遍历 bytes , 统计 每一个byte出现的次数->map[key,value]
			Map<Byte, Integer> counts = new HashMap<>();
			for (byte b : bytes) {
				Integer count = counts.get(b);
				if (count == null) { // Map还没有这个字符数据,第一次
					counts.put(b, 1);
				} else {
					counts.put(b, count + 1);
				}
			}
			
			//把每一个键值对转成一个Node 对象，并加入到nodes集合
			//遍历map
			for(Map.Entry<Byte, Integer> entry: counts.entrySet()) {
				nodes.add(new Node(entry.getKey(), entry.getValue()));
			}
			return nodes;
			
		}
		
		//可以通过List 创建对应的赫夫曼树
		private static Node createHuffmanTree(List<Node> nodes) {
			
			while(nodes.size() > 1) {
				//排序, 从小到大
				Collections.sort(nodes);
				//取出第一颗最小的二叉树
				Node leftNode = nodes.get(0);
				//取出第二颗最小的二叉树
				Node rightNode = nodes.get(1);
				//创建一颗新的二叉树,它的根节点 没有data, 只有权值
				Node parent = new Node(null, leftNode.weight + rightNode.weight);
				parent.left = leftNode;
				parent.right = rightNode;
				
				//将已经处理的两颗二叉树从nodes删除
				nodes.remove(leftNode);
				nodes.remove(rightNode);
				//将新的二叉树，加入到nodes
				nodes.add(parent);
				
			}
			//nodes 最后的结点，就是赫夫曼树的根结点
			return nodes.get(0);
			
		}
		
	
	}
	
	
	
	//创建Node ,待数据和权值
	class Node implements Comparable<Node>  {
		Byte data; // 存放数据(字符)本身，比如'a' => 97 ' ' => 32
		int weight; //权值, 表示字符出现的次数
		Node left;//
		Node right;
		public Node(Byte data, int weight) {
			
			this.data = data;
			this.weight = weight;
		}
		@Override
		public int compareTo(Node o) {
			// 从小到大排序
			return this.weight - o.weight;
		}
		
		public String toString() {
			return "Node [data = " + data + " weight=" + weight + "]";
		}
		
		//前序遍历
		public void preOrder() {
			System.out.println(this);
			if(this.left != null) {
				this.left.preOrder();
			}
			if(this.right != null) {
				this.right.preOrder();
			}
		}
	}

11.3.9 赫夫曼编码压缩文件注意事项

如果文件本身就是经过压缩处理的，那么使用赫夫曼编码再压缩效率不会有明显变化, 比如视频,ppt 等等文件
[举例压一个 .ppt]
赫夫曼编码是按字节来处理的，因此可以处理所有的文件(二进制文件、文本文件) [举例压一个.xml 文件]
如果一个文件中的内容，重复的数据不多，压缩效果也不会很明显.

11.4 二叉排序树

11.4.1 先看一个需求

给你一个数列 (7, 3, 10, 12, 5, 1, 9)，要求能够高效的完成对数据的查询和添加

11.4.2 解决方案分析

? 使用数组
数组未排序，优点：直接在数组尾添加，速度快。缺点：查找速度慢. [示意图]
数组排序，优点：可以使用二分查找，查找速度快，缺点：为了保证数组有序，在添加新数据时，找到插入位置后，后面的数据需整体移动，速度慢。[示意图]

? 使用链式存储-链表
不管链表是否有序，查找速度都慢，添加数据速度比数组快，不需要数据整体移动。[示意图]

? 使用二叉排序树

11.4.3 二叉排序树介绍

二叉排序树：BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大。
特别说明：如果有相同的值，可以将该节点放在左子节点或右子节点

比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ，对应的二叉排序树为：

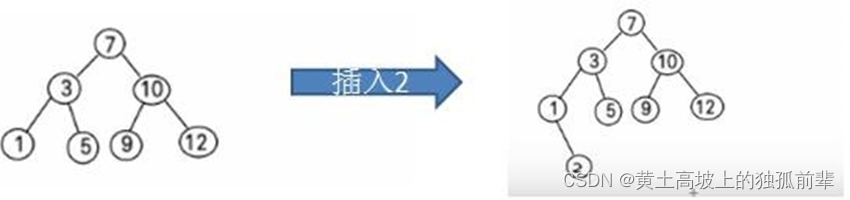
在这里插入图片描述

11.4.4 二叉排序树创建和遍历

一个数组创建成对应的二叉排序树，并使用中序遍历二叉排序树，比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) ，创建成对应的二叉排序树为 :

在这里插入图片描述

11.4.5 二叉排序树的删除

二叉排序树的删除情况比较复杂，有下面三种情况需要考虑

删除叶子节点 (比如：2, 5, 9, 12)
删除只有一颗子树的节点 (比如：1)
删除有两颗子树的节点. (比如：7, 3，10 )
操作的思路分析

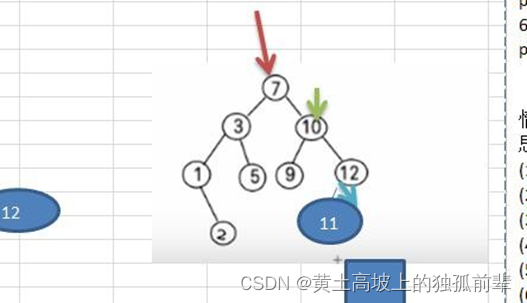
在这里插入图片描述
//对删除结点的各种情况的思路分析:

第一种情况:
删除叶子节点 (比如：2, 5, 9, 12)
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到 targetNode 的父结点 parent
(3) 确定 targetNode 是 parent 的左子结点还是右子结点
(4) 根据前面的情况来对应删除左子结点 parent.left = null
右子结点 parent.right = null;
第二种情况:
删除只有一颗子树的节点比如 1
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到 targetNode 的父结点 parent
(3) 确定 targetNode 的子结点是左子结点还是右子结点
(4) targetNode 是 parent 的左子结点还是右子结点
(5) 如果 targetNode 有左子结点
如果 targetNode 是 parent 的左子结点
parent.left = targetNode.left;
如果 targetNode 是 parent 的右子结点
parent.right = targetNode.left;
(6) 如果 targetNode 有右子结点
如果 targetNode 是 parent 的左子结点
parent.left = targetNode.right;
如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right

情况三：
删除有两颗子树的节点. (比如：7, 3，10 )
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到 targetNode 的父结点 parent
(3) 从 targetNode 的右子树找到最小的结点
(4) 用一个临时变量，将最小结点的值保存 temp = 11
(5) 删除该最小结点
(6) targetNode.value = temp

11.4.6 二叉排序树删除结点的代码实现:

package com.atguigu.binarysorttree;

public class BinarySortTreeDemo {

	public static void main(String[] args) {
		int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};
		BinarySortTree binarySortTree = new BinarySortTree();
		//循环的添加结点到二叉排序树
		for(int i = 0; i< arr.length; i++) {
			binarySortTree.add(new Node(arr[i]));
		}
		
		//中序遍历二叉排序树
		System.out.println("中序遍历二叉排序树~");
		binarySortTree.infixOrder(); // 1, 3, 5, 7, 9, 10, 12
		
		//测试一下删除叶子结点
	    
	   
	    binarySortTree.delNode(12);
	   
	 
	    binarySortTree.delNode(5);
	    binarySortTree.delNode(10);
	    binarySortTree.delNode(2);
	    binarySortTree.delNode(3);
		   
	    binarySortTree.delNode(9);
	    binarySortTree.delNode(1);
	    binarySortTree.delNode(7);
	    
		
		System.out.println("root=" + binarySortTree.getRoot());
		
		
		System.out.println("删除结点后");
		binarySortTree.infixOrder();
	}

}

//创建二叉排序树
class BinarySortTree {
	private Node root;
	
	
	
	
	public Node getRoot() {
		return root;
	}

	//查找要删除的结点
	public Node search(int value) {
		if(root == null) {
			return null;
		} else {
			return root.search(value);
		}
	}
	
	//查找父结点
	public Node searchParent(int value) {
		if(root == null) {
			return null;
		} else {
			return root.searchParent(value);
		}
	}
	
	//编写方法: 
	//1. 返回的 以node 为根结点的二叉排序树的最小结点的值
	//2. 删除node 为根结点的二叉排序树的最小结点
	/**
	 * 
	 * @param node 传入的结点(当做二叉排序树的根结点)
	 * @return 返回的 以node 为根结点的二叉排序树的最小结点的值
	 */
	public int delRightTreeMin(Node node) {
		Node target = node;
		//循环的查找左子节点，就会找到最小值
		while(target.left != null) {
			target = target.left;
		}
		//这时 target就指向了最小结点
		//删除最小结点
		delNode(target.value);
		return target.value;
	}
	
	
	//删除结点
	public void delNode(int value) {
		if(root == null) {
			return;
		}else {
			//1.需求先去找到要删除的结点  targetNode
			Node targetNode = search(value);
			//如果没有找到要删除的结点
			if(targetNode == null) {
				return;
			}
			//如果我们发现当前这颗二叉排序树只有一个结点
			if(root.left == null && root.right == null) {
				root = null;
				return;
			}
			
			//去找到targetNode的父结点
			Node parent = searchParent(value);
			//如果要删除的结点是叶子结点
			if(targetNode.left == null && targetNode.right == null) {
				//判断targetNode 是父结点的左子结点，还是右子结点
				if(parent.left != null && parent.left.value == value) { //是左子结点
					parent.left = null;
				} else if (parent.right != null && parent.right.value == value) {//是由子结点
					parent.right = null;
				}
			} else if (targetNode.left != null && targetNode.right != null) { //删除有两颗子树的节点
				int minVal = delRightTreeMin(targetNode.right);
				targetNode.value = minVal;
				
				
			} else { // 删除只有一颗子树的结点
				//如果要删除的结点有左子结点 
				if(targetNode.left != null) {
					if(parent != null) {
						//如果 targetNode 是 parent 的左子结点
						if(parent.left.value == value) {
							parent.left = targetNode.left;
						} else { //  targetNode 是 parent 的右子结点
							parent.right = targetNode.left;
						} 
					} else {
						root = targetNode.left;
					}
				} else { //如果要删除的结点有右子结点 
					if(parent != null) {
						//如果 targetNode 是 parent 的左子结点
						if(parent.left.value == value) {
							parent.left = targetNode.right;
						} else { //如果 targetNode 是 parent 的右子结点
							parent.right = targetNode.right;
						}
					} else {
						root = targetNode.right;
					}
				}
				
			}
			
		}
	}
	
	//添加结点的方法
	public void add(Node node) {
		if(root == null) {
			root = node;//如果root为空则直接让root指向node
		} else {
			root.add(node);
		}
	}
	//中序遍历
	public void infixOrder() {
		if(root != null) {
			root.infixOrder();
		} else {
			System.out.println("二叉排序树为空，不能遍历");
		}
	}
}

//创建Node结点
class Node {
	int value;
	Node left;
	Node right;
	public Node(int value) {
		
		this.value = value;
	}
	
	
	//查找要删除的结点
	/**
	 * 
	 * @param value 希望删除的结点的值
	 * @return 如果找到返回该结点，否则返回null
	 */
	public Node search(int value) {
		if(value == this.value) { //找到就是该结点
			return this;
		} else if(value < this.value) {//如果查找的值小于当前结点，向左子树递归查找
			//如果左子结点为空
			if(this.left  == null) {
				return null;
			}
			return this.left.search(value);
		} else { //如果查找的值不小于当前结点，向右子树递归查找
			if(this.right == null) {
				return null;
			}
			return this.right.search(value);
		}
		
	}
	//查找要删除结点的父结点
	/**
	 * 
	 * @param value 要找到的结点的值
	 * @return 返回的是要删除的结点的父结点，如果没有就返回null
	 */
	public Node searchParent(int value) {
		//如果当前结点就是要删除的结点的父结点，就返回
		if((this.left != null && this.left.value == value) || 
				(this.right != null && this.right.value == value)) {
			return this;
		} else {
			//如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
			if(value < this.value && this.left != null) {
				return this.left.searchParent(value); //向左子树递归查找
			} else if (value >= this.value && this.right != null) {
				return this.right.searchParent(value); //向右子树递归查找
			} else {
				return null; // 没有找到父结点
			}
		}
		
	}
	
	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}


	//添加结点的方法
	//递归的形式添加结点，注意需要满足二叉排序树的要求
	public void add(Node node) {
		if(node == null) {
			return;
		}
		
		//判断传入的结点的值，和当前子树的根结点的值关系
		if(node.value < this.value) {
			//如果当前结点左子结点为null
			if(this.left == null) {
				this.left = node;
			} else {
				//递归的向左子树添加
				this.left.add(node);
			}
		} else { //添加的结点的值大于 当前结点的值
			if(this.right == null) {
				this.right = node;
			} else {
				//递归的向右子树添加
				this.right.add(node);
			}
			
		}
	}
	
	//中序遍历
	public void infixOrder() {
		if(this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if(this.right != null) {
			this.right.infixOrder();
		}
	}
	
}

11.4.7 课后练习：完成老师代码，并使用第二种方式来解决

如果我们从左子树找到最大的结点，然后前面的思路完成.

11.5 平衡二叉树(AVL 树)

11.5.1 看一个案例(说明二叉排序树可能的问题)

给你一个数列{1,2,3,4,5,6}，要求创建一颗二叉排序树(BST), 并分析问题所在.
? 左边 BST 存在的问题分析:

左子树全部为空，从形式上看，更像一个单链表.
插入速度没有影响
查询速度明显降低(因为需要依次比较), 不能发挥 BST

的优势，因为每次还需要比较左子树，其查询速度比单链表还慢
4) 解决方案-平衡二叉树(AVL)

11.5.2 基本介绍

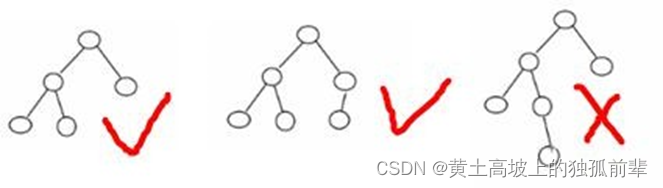
平衡二叉树也叫平衡二叉搜索树（Self-balancing binary search tree）又被称为 AVL 树，可以保证查询效率较高。
具有以下特点：它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
举例说明, 看看下面哪些 AVL 树, 为什么?

11.5.3 应用案例-单旋转(左旋转)

要求: 给你一个数列，创建出对应的平衡二叉树.数列 {4,3,6,5,7,8}
思路分析(示意图)

代码实现

 //左旋转方法
	private void leftRotate() {
		
		//创建新的结点，以当前根结点的值
		Node newNode = new Node(value);
		//把新的结点的左子树设置成当前结点的左子树
		newNode.left = left;
		//把新的结点的右子树设置成带你过去结点的右子树的左子树
		newNode.right = right.left;
		//把当前结点的值替换成右子结点的值
		value = right.value;
		//把当前结点的右子树设置成当前结点右子树的右子树
		right = right.right;
		//把当前结点的左子树(左子结点)设置成新的结点
		left = newNode;
		
		
	}

11.5.4 应用案例-单旋转(右旋转)

要求: 给你一个数列，创建出对应的平衡二叉树.数列 {10,12, 8, 9, 7, 6}
思路分析(示意图)

代码实现

//右旋转
private void rightRotate() {
	Node newNode = new Node(value);
	newNode.right = right;
	newNode.left = left.right;
	value = left.value;
	left = left.left;
	right = newNode;
}

11.5.5 应用案例-双旋转

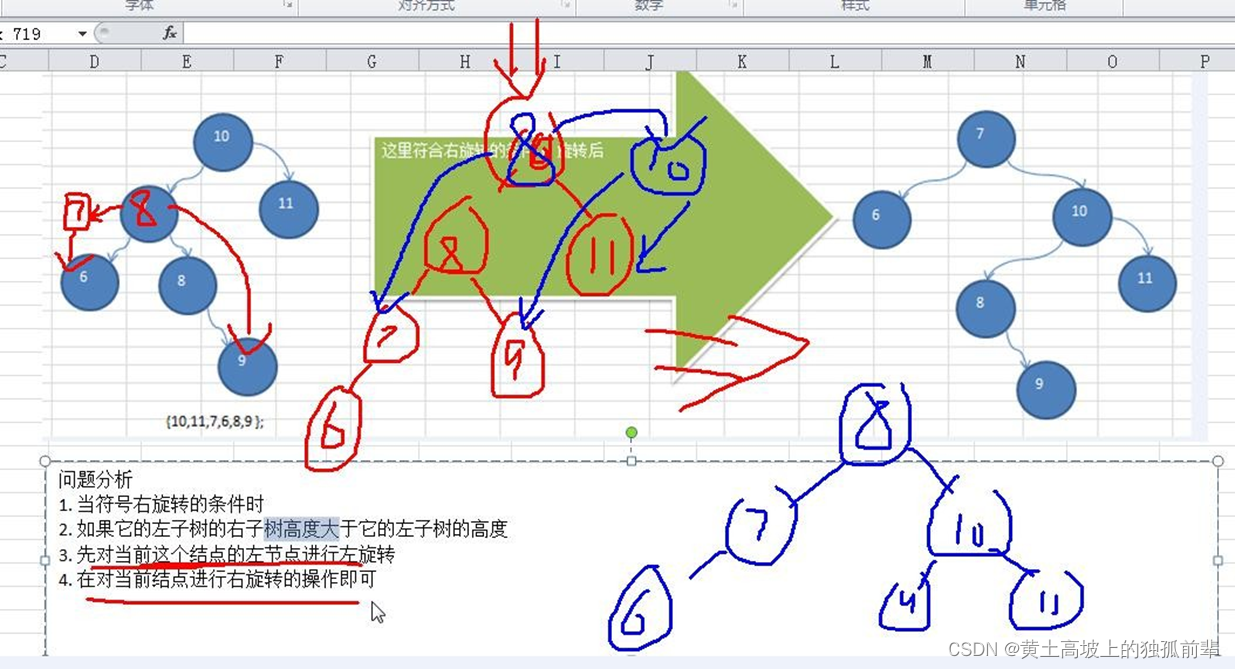
前面的两个数列，进行单旋转(即一次旋转)就可以将非平衡二叉树转成平衡二叉树,但是在某些情况下，单旋转不能完成平衡二叉树的转换。比如数列
int[] arr = { 10, 11, 7, 6, 8, 9 }; 运行原来的代码可以看到，并没有转成 AVL 树. int[] arr = {2,1,6,5,7,3}; // 运行原来的代码可以看到，并没有转成 AVL 树

问题分析
解决思路分析

当符号右旋转的条件时
如果它的左子树的右子树高度大于它的左子树的高度
先对当前这个结点的左节点进行左旋转
在对当前结点进行右旋转的操作即可

代码实现[AVL 树的汇总代码(完整代码)]

 package com.atguigu.avl;



public class AVLTreeDemo {

	public static void main(String[] args) {
		//int[] arr = {4,3,6,5,7,8};
		//int[] arr = { 10, 12, 8, 9, 7, 6 };
		int[] arr = { 10, 11, 7, 6, 8, 9 };  
		//创建一个 AVLTree对象
		AVLTree avlTree = new AVLTree();
		//添加结点
		for(int i=0; i < arr.length; i++) {
			avlTree.add(new Node(arr[i]));
		}
		
		//遍历
		System.out.println("中序遍历");
		avlTree.infixOrder();
		
		System.out.println("在平衡处理~~");
		System.out.println("树的高度=" + avlTree.getRoot().height()); //3
		System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight()); // 2
		System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight()); // 2
		System.out.println("当前的根结点=" + avlTree.getRoot());//8
		
		
	}

}

// 创建AVLTree
class AVLTree {
	private Node root;

	public Node getRoot() {
		return root;
	}

	// 查找要删除的结点
	public Node search(int value) {
		if (root == null) {
			return null;
		} else {
			return root.search(value);
		}
	}

	// 查找父结点
	public Node searchParent(int value) {
		if (root == null) {
			return null;
		} else {
			return root.searchParent(value);
		}
	}

	// 编写方法:
	// 1. 返回的 以node 为根结点的二叉排序树的最小结点的值
	// 2. 删除node 为根结点的二叉排序树的最小结点
	/**
	 * 
	 * @param node
	 *            传入的结点(当做二叉排序树的根结点)
	 * @return 返回的 以node 为根结点的二叉排序树的最小结点的值
	 */
	public int delRightTreeMin(Node node) {
		Node target = node;
		// 循环的查找左子节点，就会找到最小值
		while (target.left != null) {
			target = target.left;
		}
		// 这时 target就指向了最小结点
		// 删除最小结点
		delNode(target.value);
		return target.value;
	}

	// 删除结点
	public void delNode(int value) {
		if (root == null) {
			return;
		} else {
			// 1.需求先去找到要删除的结点 targetNode
			Node targetNode = search(value);
			// 如果没有找到要删除的结点
			if (targetNode == null) {
				return;
			}
			// 如果我们发现当前这颗二叉排序树只有一个结点
			if (root.left == null && root.right == null) {
				root = null;
				return;
			}

			// 去找到targetNode的父结点
			Node parent = searchParent(value);
			// 如果要删除的结点是叶子结点
			if (targetNode.left == null && targetNode.right == null) {
				// 判断targetNode 是父结点的左子结点，还是右子结点
				if (parent.left != null && parent.left.value == value) { // 是左子结点
					parent.left = null;
				} else if (parent.right != null && parent.right.value == value) {// 是由子结点
					parent.right = null;
				}
			} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
				int minVal = delRightTreeMin(targetNode.right);
				targetNode.value = minVal;

			} else { // 删除只有一颗子树的结点
				// 如果要删除的结点有左子结点
				if (targetNode.left != null) {
					if (parent != null) {
						// 如果 targetNode 是 parent 的左子结点
						if (parent.left.value == value) {
							parent.left = targetNode.left;
						} else { // targetNode 是 parent 的右子结点
							parent.right = targetNode.left;
						}
					} else {
						root = targetNode.left;
					}
				} else { // 如果要删除的结点有右子结点
					if (parent != null) {
						// 如果 targetNode 是 parent 的左子结点
						if (parent.left.value == value) {
							parent.left = targetNode.right;
						} else { // 如果 targetNode 是 parent 的右子结点
							parent.right = targetNode.right;
						}
					} else {
						root = targetNode.right;
					}
				}

			}

		}
	}

	// 添加结点的方法
	public void add(Node node) {
		if (root == null) {
			root = node;// 如果root为空则直接让root指向node
		} else {
			root.add(node);
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (root != null) {
			root.infixOrder();
		} else {
			System.out.println("二叉排序树为空，不能遍历");
		}
	}
}

// 创建Node结点
class Node {
	int value;
	Node left;
	Node right;

	public Node(int value) {

		this.value = value;
	}

	// 返回左子树的高度
	public int leftHeight() {
		if (left == null) {
			return 0;
		}
		return left.height();
	}

	// 返回右子树的高度
	public int rightHeight() {
		if (right == null) {
			return 0;
		}
		return right.height();
	}

	// 返回 以该结点为根结点的树的高度
	public int height() {
		return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
	}
	
	//左旋转方法
	private void leftRotate() {
		
		//创建新的结点，以当前根结点的值
		Node newNode = new Node(value);
		//把新的结点的左子树设置成当前结点的左子树
		newNode.left = left;
		//把新的结点的右子树设置成带你过去结点的右子树的左子树
		newNode.right = right.left;
		//把当前结点的值替换成右子结点的值
		value = right.value;
		//把当前结点的右子树设置成当前结点右子树的右子树
		right = right.right;
		//把当前结点的左子树(左子结点)设置成新的结点
		left = newNode;
		
		
	}
	
	//右旋转
	private void rightRotate() {
		Node newNode = new Node(value);
		newNode.right = right;
		newNode.left = left.right;
		value = left.value;
		left = left.left;
		right = newNode;
	}

	// 查找要删除的结点
	/**
	 * 
	 * @param value
	 *            希望删除的结点的值
	 * @return 如果找到返回该结点，否则返回null
	 */
	public Node search(int value) {
		if (value == this.value) { // 找到就是该结点
			return this;
		} else if (value < this.value) {// 如果查找的值小于当前结点，向左子树递归查找
			// 如果左子结点为空
			if (this.left == null) {
				return null;
			}
			return this.left.search(value);
		} else { // 如果查找的值不小于当前结点，向右子树递归查找
			if (this.right == null) {
				return null;
			}
			return this.right.search(value);
		}

	}

	// 查找要删除结点的父结点
	/**
	 * 
	 * @param value
	 *            要找到的结点的值
	 * @return 返回的是要删除的结点的父结点，如果没有就返回null
	 */
	public Node searchParent(int value) {
		// 如果当前结点就是要删除的结点的父结点，就返回
		if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
			return this;
		} else {
			// 如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
			if (value < this.value && this.left != null) {
				return this.left.searchParent(value); // 向左子树递归查找
			} else if (value >= this.value && this.right != null) {
				return this.right.searchParent(value); // 向右子树递归查找
			} else {
				return null; // 没有找到父结点
			}
		}

	}

	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	// 添加结点的方法
	// 递归的形式添加结点，注意需要满足二叉排序树的要求
	public void add(Node node) {
		if (node == null) {
			return;
		}

		// 判断传入的结点的值，和当前子树的根结点的值关系
		if (node.value < this.value) {
			// 如果当前结点左子结点为null
			if (this.left == null) {
				this.left = node;
			} else {
				// 递归的向左子树添加
				this.left.add(node);
			}
		} else { // 添加的结点的值大于 当前结点的值
			if (this.right == null) {
				this.right = node;
			} else {
				// 递归的向右子树添加
				this.right.add(node);
			}

		}
		
		//当添加完一个结点后，如果: (右子树的高度-左子树的高度) > 1 , 左旋转
		if(rightHeight() - leftHeight() > 1) {
			//如果它的右子树的左子树的高度大于它的右子树的右子树的高度
			if(right != null && right.leftHeight() > right.rightHeight()) {
				//先对右子结点进行右旋转
				right.rightRotate();
				//然后在对当前结点进行左旋转
				leftRotate(); //左旋转..
			} else {
				//直接进行左旋转即可
				leftRotate();
			}
			return ; //必须要!!!
		}
		
		//当添加完一个结点后，如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
		if(leftHeight() - rightHeight() > 1) {
			//如果它的左子树的右子树高度大于它的左子树的高度
			if(left != null && left.rightHeight() > left.leftHeight()) {
				//先对当前结点的左结点(左子树)->左旋转
				left.leftRotate();
				//再对当前结点进行右旋转
				rightRotate();
			} else {
				//直接进行右旋转即可
				rightRotate();
			}
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if (this.right != null) {
			this.right.infixOrder();
		}
	}

}

文章来源:https://blog.csdn.net/lihuazaizheli/article/details/135587955
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

第 11 章 树结构实际应用

文章目录

11.1 堆排序

11.1.1 堆排序基本介绍

11.1.2 堆排序基本思想

11.1.3 堆排序步骤图解说明

11.1.4 堆排序代码实现

11.2 赫夫曼树

11.2.1 基本介绍

11.2.2 赫夫曼树几个重要概念和举例说明

11.2.3 赫夫曼树创建思路图解

11.2.4 赫夫曼树的代码实现

11.3 赫夫曼编码

11.3.1 基本介绍

11.3.2 原理剖析

11.3.3 最佳实践-数据压缩(创建赫夫曼树)

11.3.4 最佳实践-数据压缩(生成赫夫曼编码和赫夫曼编码后的数据)

11.3.5 最佳实践-数据解压(使用赫夫曼编码解码)

11.3.6 最佳实践-文件压缩

11.3.7 最佳实践-文件解压(文件恢复)

11.3.8 代码汇总，把前面所有的方法放在一起

11.3.9 赫夫曼编码压缩文件注意事项

11.4 二叉排序树

11.4.1 先看一个需求

11.4.2 解决方案分析

11.4.3 二叉排序树介绍

11.4.4 二叉排序树创建和遍历

11.4.5 二叉排序树的删除

11.4.6 二叉排序树删除结点的代码实现:

11.4.7 课后练习：完成老师代码，并使用第二种方式来解决

11.5 平衡二叉树(AVL 树)

11.5.1 看一个案例(说明二叉排序树可能的问题)

11.5.2 基本介绍

11.5.3 应用案例-单旋转(左旋转)

11.5.4 应用案例-单旋转(右旋转)

11.5.5 应用案例-双旋转

第 11 章树结构实际应用