7.12全排列②（LC47-M）

算法：

这道题目和46.全排列?(opens new window)的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

所以就是多了个去重操作。

还是一样的套路：

先排序：

Arrays.sort(nums);

再去重：

// used[i - 1] == true，说明同?树?nums[i - 1]使?过
// used[i - 1] == false，说明同?树层nums[i - 1]使?过
// 如果同?树层nums[i - 1]使?过则直接跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }

注意：

（1）其实used[i - 1] == false也行，而used[i - 1] == true也行

用输入: [1,1,1] 来举一个例子：

树层上去重(used[i - 1] == false)，的树形结构如下：

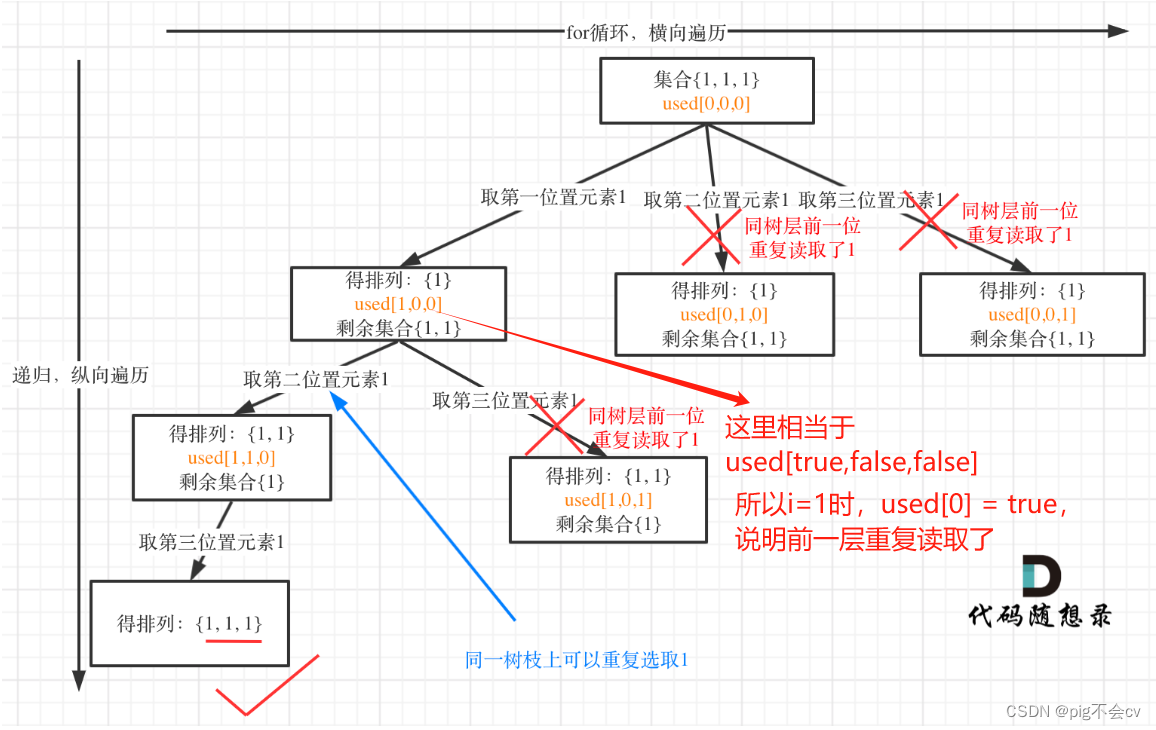
树枝上去重（used[i - 1] == true）的树型结构如下：

树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索。

所以实际去重时，用used[i - 1] == false

（2）为什么一定要加上?used[i - 1] == false或者used[i - 1] == true ？

因为 used[i - 1] 要一直是 true 或者一直是false 才可以，而不是 一会是true 一会又是false。 所以这个条件要写上。

正确代码：

class Solution {
    List<List<Integer>> result = new LinkedList<>();
    List<Integer> path = new LinkedList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
    boolean[] used2 = new boolean[nums.length]; 
    Arrays.fill(used2, false);
    Arrays.sort(nums);  
    backtracking (nums, used2);
    return result;
    }

    void backtracking (int[] nums, boolean[] used) {
    //确定终止条件
    if (path.size() == nums.length) {
        result.add (new LinkedList(path));
        return;
    }
    //单层递归逻辑，排序的i都从0开始了
    for(int i=0; i < nums.length; i++){
    //去重
    if (i>0 && nums[i] == nums[i-1] && used[i-1] == false) continue;
    if (used[i] == true) continue;
    //如果同?树?nums[i]没使?过开始处理
    
    //标记用过的数字
    used[i] = true;
    path.add(nums[i]);
    //递归
    backtracking (nums, used);
    //回溯，先入后出
    //先标记的used，那回溯时，used就后改
    path.removeLast();
    used[i] = false;
    
    }
    }
}

注意：

（1）在permuteUnique中新建used2后，要将其用false填满（Arrays.fill(used2, false);），这样才能符合后面backtracking的逻辑

（2）去重时，used[i-1] == false而不是used[i] == false，因为used[i]的默认值本来就是false，只有使用过的used[i-1]才可能被标记为true

时间空间复杂度：