代码随想录刷题题Day17

刷题的第十七天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day17 任务
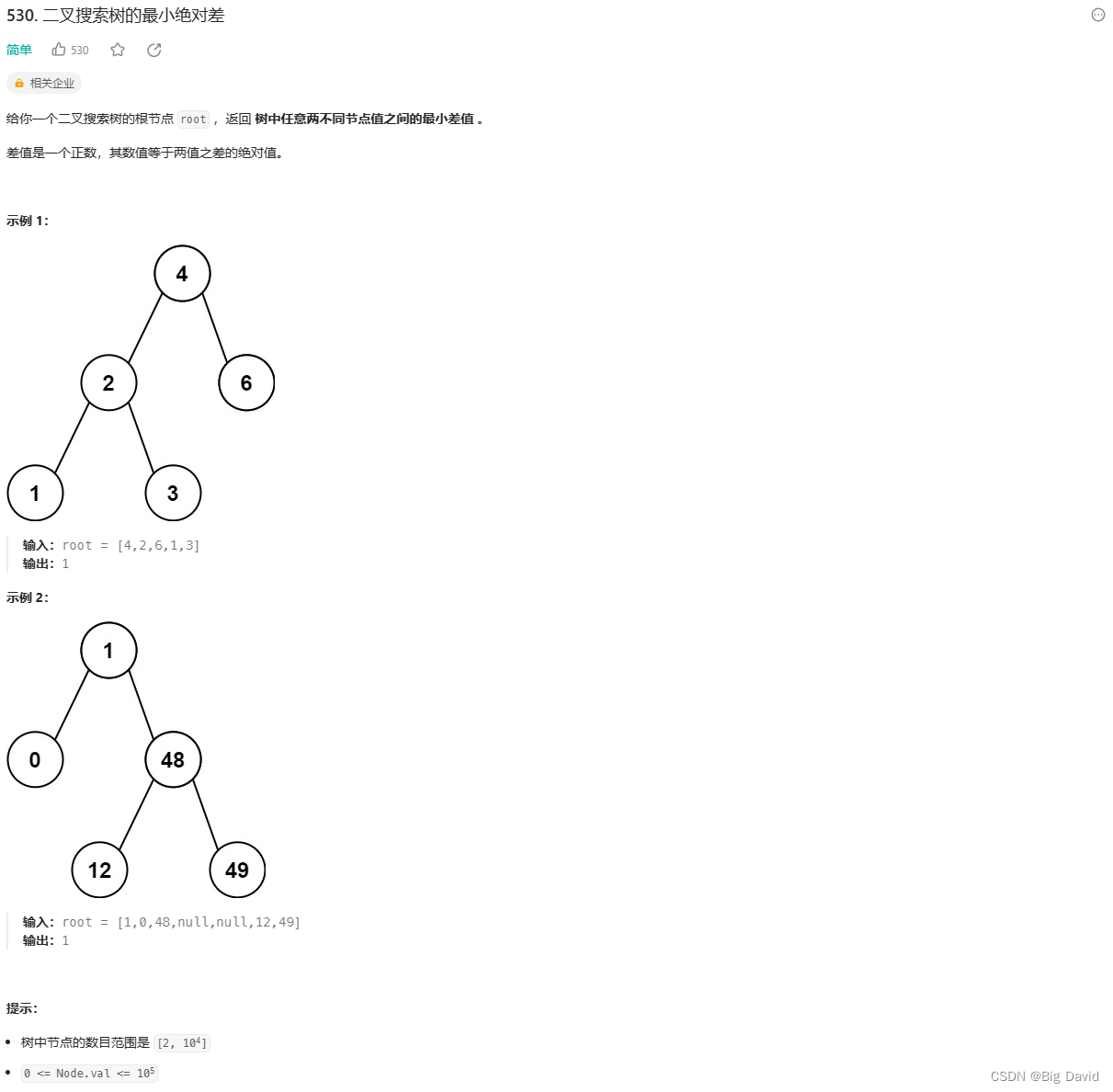
● 530.二叉搜索树的最小绝对差
● 501.二叉搜索树中的众数
● 236. 二叉树的最近公共祖先

1 二叉搜索树的最小绝对差

530.二叉搜索树的最小绝对差

利用二叉搜索树的特性：二叉搜索树是有序的

遇到在二叉搜索树上求最值，求差值，就把它想象成在一个有序数组上求最值，求差值

递归法
二叉搜索树采用中序遍历，就是一个有序数组
思路1：

把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值

class Solution {
public:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val);// 将二叉搜索树转换为有序数组
        traversal(root->right);
    }
    int getMinimumDifference(TreeNode* root) {
        vec.clear();
        traversal(root);
        int result = INT_MAX;
        for (int i = 1; i < vec.size(); i++) {// 统计有序数组的最小差值
            result = min(result, vec[i] - vec[i - 1]);
        }
        return result;
    }
};

思路2：

在二叉搜素树中序遍历的过程中就可以直接计算
用一个pre节点记录cur节点的前一个节点

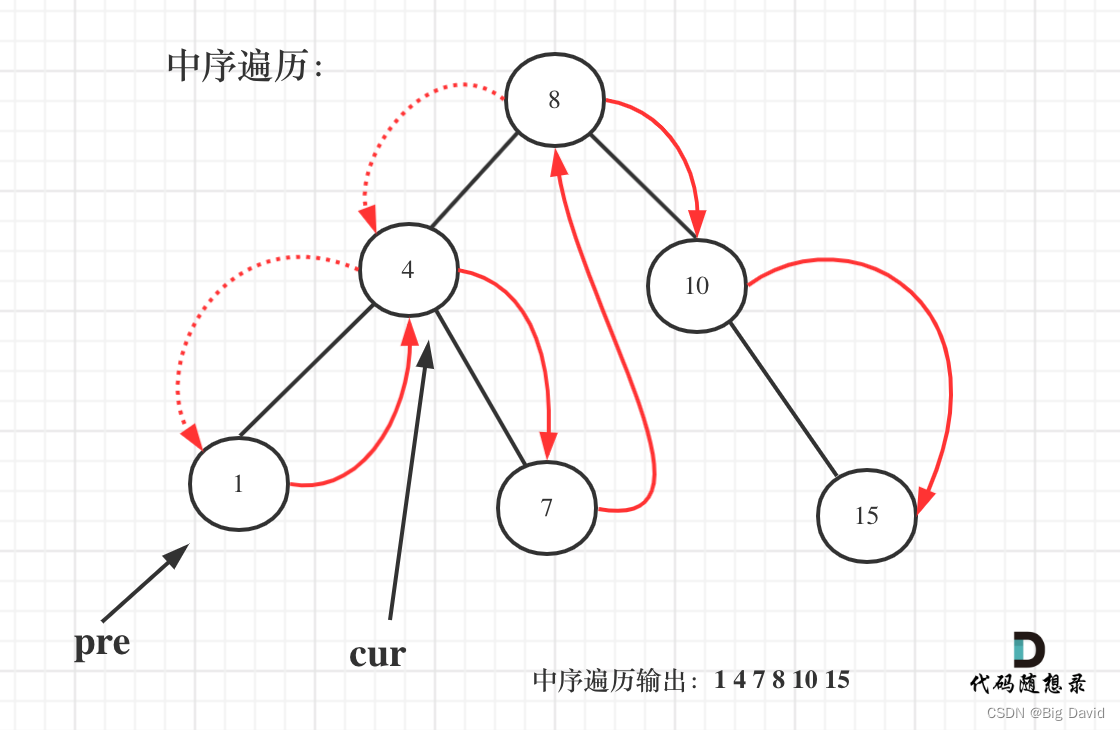
class Solution {
public:
    int result = INT_MAX;
    TreeNode* pre = NULL;
    void traversal(TreeNode* cur) {
        if (cur == NULL) return;
        traversal(cur->left);// 左
        if (pre != NULL) {// 中
            result = min(result, cur->val - pre->val);
        }
        pre = cur;// 记录前一个
        traversal(cur->right);// 右
    }
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return result;
    }
};

2 二叉搜索树中的众数

501.二叉搜索树中的众数

递归法
二叉搜索树：既然是搜索树，它中序遍历就是有序的

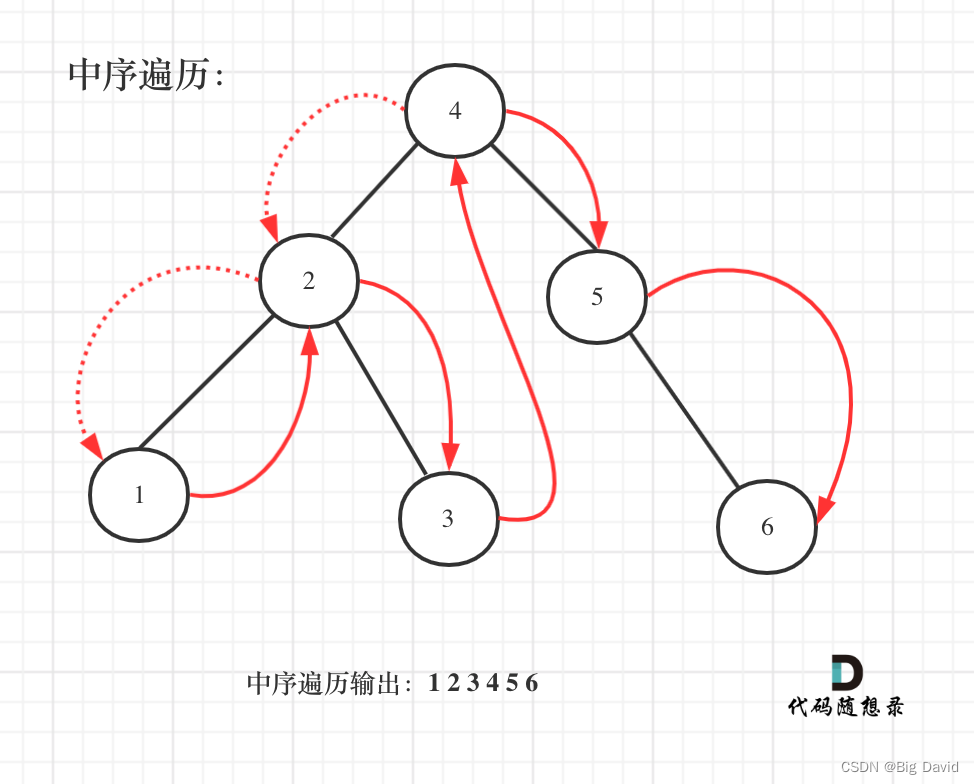
中序遍历代码：

void traversal(TreeNode* cur) {
	if (cur == NULL) return;
	traversal(cur->left); // 左
	处理节点               // 中
	traversal(cur->right);// 右
	return;
}

处理节点逻辑：

if (pre == NULL) count = 1;// 第一个节点
else if (pre->val == cur->val) count++;// 与前一个节点数值相同
else count = 1;// 与前一个节点数值不同
pre = cur;// 更新上一个节点

只需要遍历一次就可以找到所有的众数

频率count 等于 maxCount（最大频率），把这个元素加入到结果集中（以下代码为result数组）
频率count 大于 maxCount的时候，不仅要更新maxCount，而且要清空结果集（以下代码为result数组），因为结果集之前的元素都失效

if (count == maxCount) {
	result.push_back(cur->val);
}
if (count > maxCount) {// 如果计数大于最大值
	maxCount = count;// 更新最大频率
	result.clear();// 清空result，之前result里的元素都失效
	result.push_back(cur->val);
}

C++：

class Solution {
public:
    int count = 0;   // 统计频率
    int maxCount = 0;// 最大频率
    vector<int> result;
    TreeNode* pre = NULL;
    void traversal(TreeNode* cur) {
        if (cur == NULL) return;
        traversal(cur->left); // 左
        // 中
        if (pre == NULL) count = 1;
        else if (pre->val == cur->val) count++;
        else count = 1;
        pre = cur;// 记录前一个节点
        if (count == maxCount) result.push_back(cur->val);
        if (count > maxCount) {
            maxCount = count;
            result.clear();
            result.push_back(cur->val);
        }
        traversal(cur->right);// 右
        return;
    }
    vector<int> findMode(TreeNode* root) {
        traversal(root);
        return result;
    }
};

不是二叉搜索树，最直观的方法把这个树都遍历，用map统计频率，把频率排个序，最后取前面高频的元素的集合

（1）遍历这个树，用map统计频率

用哪种遍历顺序都可以

// map<int, int> key:元素，value:出现频率
void traversal(TreeNode* cur, unordered_map<int, int>& map) {// 前序遍历
	if (cur == NULL) return;
	map[cur->val]++;
	traversal(cur->left, map);
	traversal(cur->right, map);
	return;
}

（2）把统计的出来的出现频率（即map中的value）排个序

把map转化数组即vector，再进行排序，当然vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率

bool static cmp(const pair<int, int>& a, const pair<int, int>& b) {
	return a.second > b.second;// 按照频率从大到小排序
}
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp);// 给频率排个序

（3）取前面高频的元素

数组vector中已经是存放着按照频率排好序的pair，把前面高频的元素取出来

result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {
	if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
	else break;
}
return result;

C++：

class Solution {
public:
    void traversal(TreeNode* cur, unordered_map<int, int>& map) {// 前序遍历
        if (cur == NULL) return;
        map[cur->val]++;// 统计元素频率
        traversal(cur->left, map);
        traversal(cur->right, map);
        return;
    }
    bool static cmp(const pair<int, int>& a, const pair<int, int>& b) {
        return a.second > b.second;
    }
    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> map;// key:元素，value:出现频率
        vector<int> result;
        if (root == NULL) return result;
        traversal(root, map);
        vector<pair<int, int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);// 给频率排个序
        result.push_back(vec[0].first);
        // 取最高的放到result数组中
        for (int i = 1; i < vec.size(); i++) {
            if (vec[0].second == vec[i].second) {
                result.push_back(vec[i].first);
            }
            else break;
        }
        return result;
    }
};

3 二叉树的最近公共祖先

236. 二叉树的最近公共祖先
最近公共祖先的定义：

对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）

思路：
二叉树如何可以自底向上查找？回溯

后序遍历（左右中）就是天然的回溯，可以根据左右子树的返回值，来处理中节点的逻辑

最容易的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先

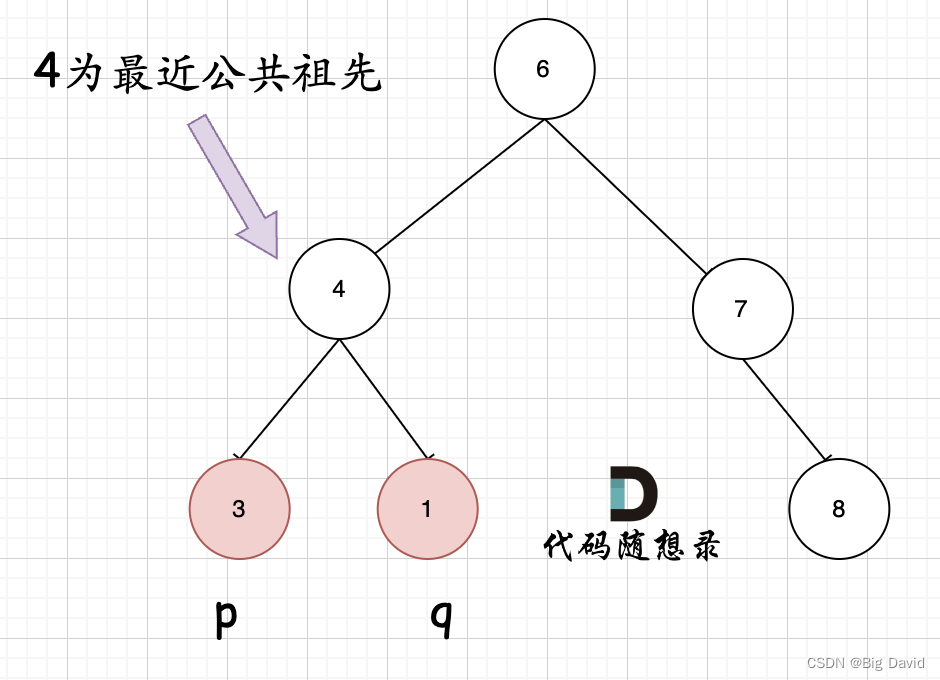
判断逻辑：如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果左右子树的返回值都不为空，说明此时的中节点，一定是q 和p的最近祖先

容易忽略的情况：

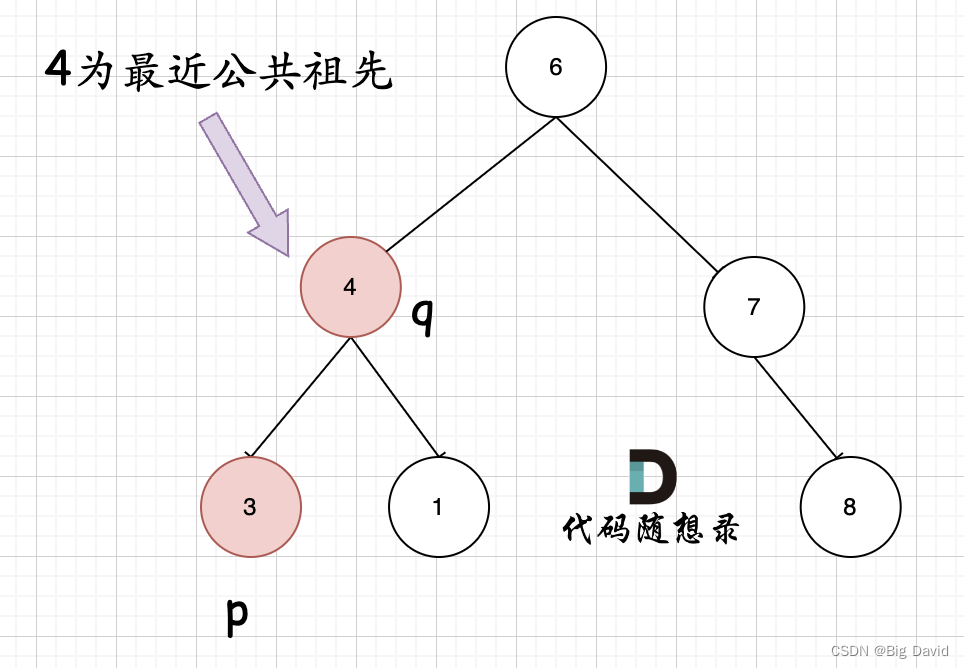
递归法
（1）确定递归函数返回值以及参数
返回值：最近公共节点，TreeNode*
参数：根节点、p、q

TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q)

（2）确定终止条件

遇到空的话，因为树都是空了，所以返回空
如果 root == q，或者 root == p，说明找到 q p ，则将其返回

if (root == q || root == q || root == NULL) return root;

（3）确定单层递归逻辑

本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题依然要遍历树的所有节点

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

1. 搜索一条边

if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;

2. 搜索整棵树

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

TreeNode* left = traversal(root->left, p, q);
TreeNode* right = traversal(root->right, p, q);

(1) 如果left和right都不为空，说明此时root就是最近公共节点
(2) 如果left为空，right不为空，就返回right，说明目标节点是通过right返回的。

if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else return NULL;

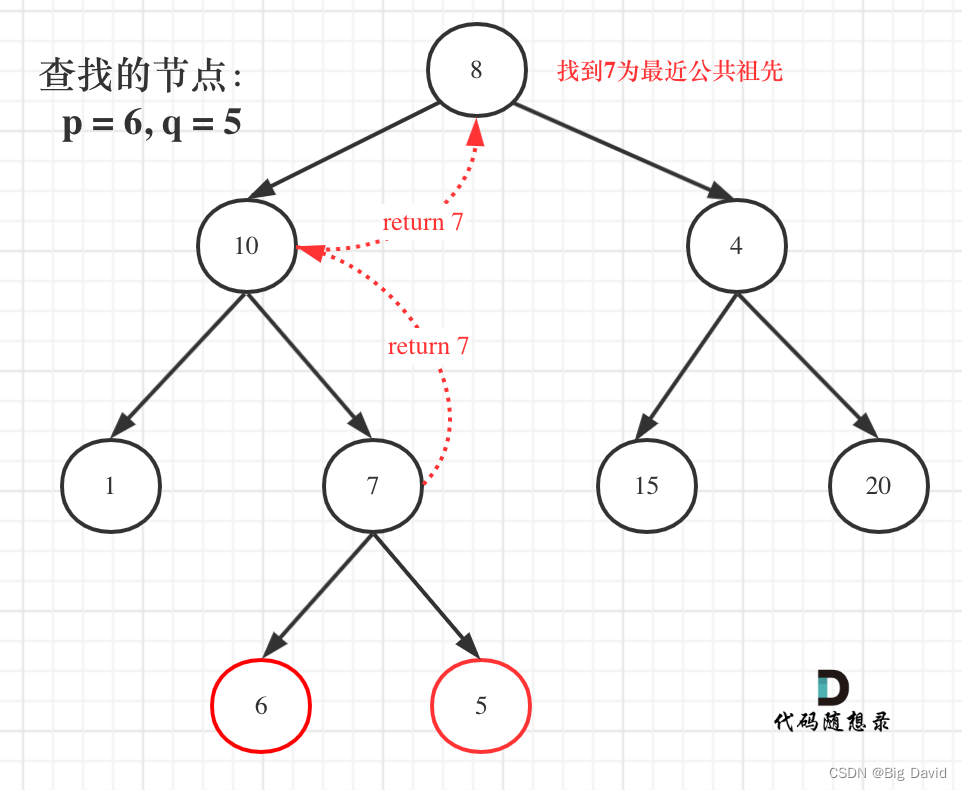
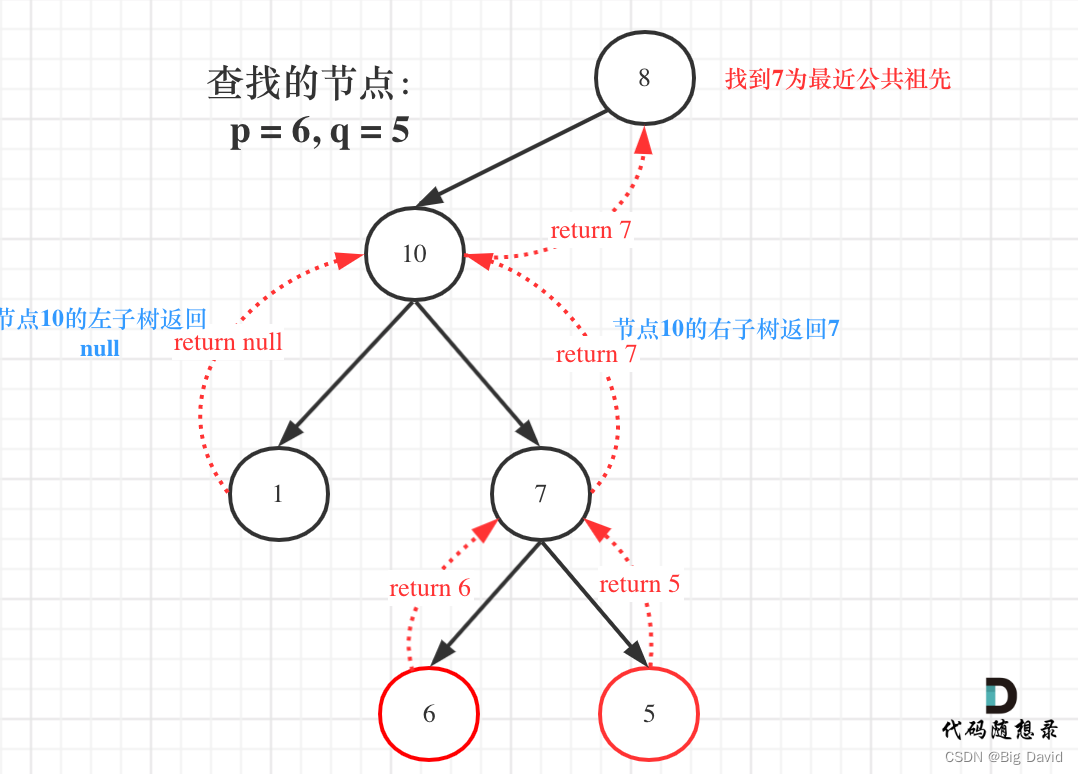
寻找最小公共祖先，完整流程图:

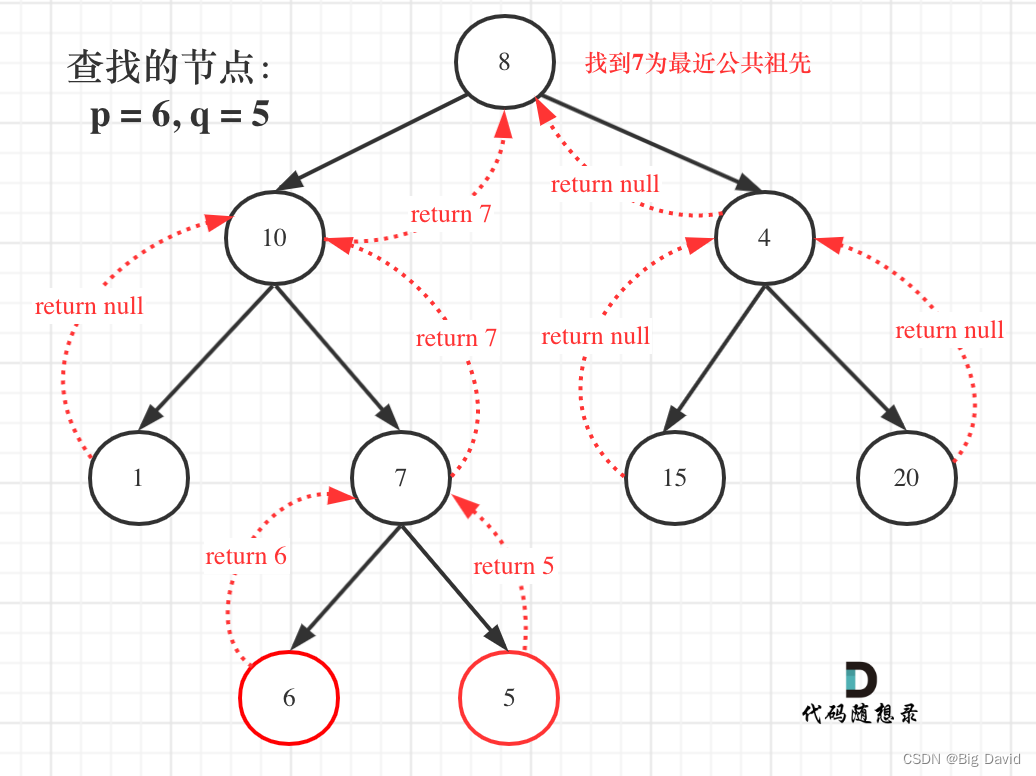
C++：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == p || root == q || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);// 左
        TreeNode* right = lowestCommonAncestor(root->right, p, q);// 右
        // 中
        if (left != NULL && right != NULL) return root;
        if (left == NULL && right != NULL) return right;
        else if (left != NULL && right == NULL) return left;
        else return NULL;
    }
};

精简C++：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == p || root == q || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != NULL && right != NULL) return root;
        if (left == NULL) return right;
        return left;
    }
};

总结:

（1）求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式
（2）在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断

---

鼓励坚持十八天的自己😀😀😀