基于MATLAB的泊松分布，正态分布与伽玛分布（附完整代码与例题）

目录

一. 泊松分布

1.1 理论部分

1.2 MATLAB函数模型

1.3 例题

二. 正态分布

2.1 理论部分

2.2 MATLAB函数模型

2.3 例题

三. 伽玛分布

3.1 理论部分

3.2 MATLAB函数模型

3.3 例题

---

一. 泊松分布

1.1 理论部分

Poisson分布是离散的，其x值只能取自然数。Poisson分布的概率密度函数如下：

其中是一个固定的正整数常数。在泊松分布中，参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。以下情况可以构建泊松分布模型：

• 某一服务设施在一定时间内到达的人数
• 电话交换机接到呼叫的次数
• 汽车站台的候客人数
• 机器出现的故障数
• 自然灾害发生的次数

?

1.2 MATLAB函数模型

泊松分布的概率密度函数，在MATLAB中可以直接调用：

y=poisspdf(x,lambda);

%给定x与lambda的值，就可以直接求该点的概率密度值

分布函数（累积概率函数），在MATLAB中可以直接调用：

F=poisscdf(x,lambda)

如果给定分布函数值，反过来求x，则需要调用逆概率分布函数：

x=poissinv(F,lambda)

MATLAB本身非常适合用来处理向量和矩阵，所以，如果输入的x为一个向量的话，那么输出的y则是x各个点处的概率密度函数值。

1.3 例题

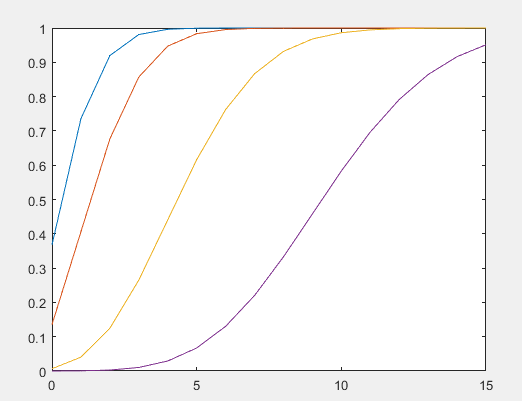
绘制时，泊松分布的概率密度函数与概率分布函数曲线图。

MATLAB代码：

x=[0:15]'; 
%x为0~15之间的整数，注意需要通过'转为列向量
y1=[]; y2=[]; 
%要画两个图像
lam1=[1,2,5,10];
%lambda确定了，泊松分布就确定了
for i=1:length(lam1) %lam1的长度为4
    y1=[y1,poisspdf(x,lam1(i))]; %lam1(i)代表调用集合lam1中的第i个元素
    y2=[y2,poisscdf(x,lam1(i))];
end
plot(x,y1), figure; %figure命令可让其画两个图
plot(x,y2)

注意题目要求是画曲线，所以需要将这些点连起来。

泊松概率密度函数图：

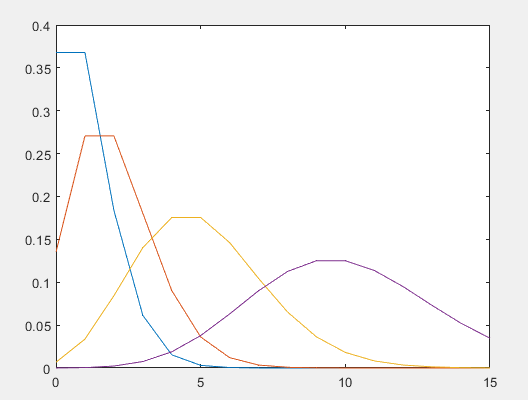
泊松分布的概率分布函数图：

二. 正态分布

2.1 理论部分

正态分布的概率密度函数如下：

其中代表均值，代表方差。

2.2 MATLAB函数模型

正态分布的概率密度函数，在MATLAB中可以直接调用：

y=normpdf(x,mu,sigma);

%给定x,mu,sigma的值，就可以直接求该点的概率密度值
%注意函数调用格式中的sigma使用的是标准差

分布函数（累积概率函数），在MATLAB中可以直接调用：

F=normcdf(x,mu,sigma);

如果给定分布函数值，反过来求x，则需要调用逆概率分布函数：

x=norminv(F,mu,sigma);

2.3 例题

分别绘制出为(-1,1),(0,0.1),(0,1),(0,10),(1,1)时，正态分布的概率密度函数与分布函数曲线。

MATLAB代码：

x=[-5:.02:5]'; 
y1=[]; 
y2=[];
mu1=[-1,0,0,0,1]; 
sig1=[1,0.1,1,10,1]; sig1=sqrt(sig1); %注意函数调用的是标准差
for i=1:length(mu1)   %length(mu1)=5    
    y1=[y1,normpdf(x,mu1(i),sig1(i))];
    y2=[y2,normcdf(x,mu1(i),sig1(i))];  
end
plot(x,y1), figure; 
plot(x,y2)

正态分布的概率密度函数图：

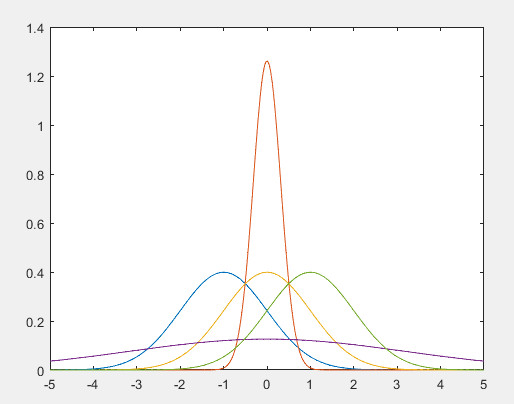
根据对称轴的值，也就是均值的大小可以对应曲线代表的正态分布。方差越大，曲线越胖。

分布函数曲线图：

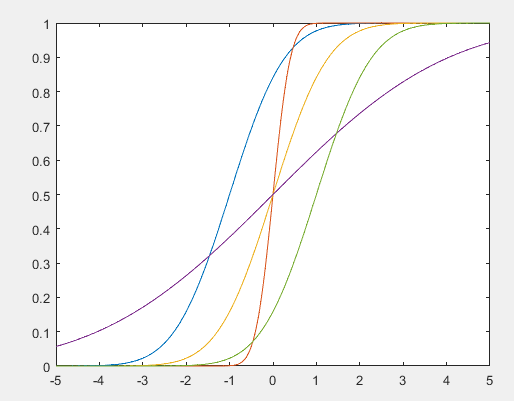
函数严格单调递增。

三. 伽玛分布

3.1 理论部分

观察相邻两个事件之间时间间隔的分布情况，或者隔k个事件的时间间隔的分布情况。根据概率论，事件之间的时间间隔应符合伽玛分布，由于时间间隔可以是任意数值，因此伽玛分布是一种连续概率分布。又因为时间间隔不可能为负数，所以伽玛分布的x需要非负。

伽玛分布有的时候也会写做分布，其概率密度函数为：

伽玛分布需要提前确定两个参数：a与.

上个式子中：

在MATLAB可以调用积分函数来计算该值，也可以直接调用gamma()函数来计算，两种途径都可以。

该积分属于指数积分类型，有三个常用的结论：

3.2 MATLAB函数模型

与泊松分布和正态分布类似，此处也有对应的三个函数，就不过多啰嗦了：

%概率密度函数
y=gampdf(x,a,lambda)

%概率分布函数
F=gamcdf(x,a,lambda)

%逆概率分布函数
x=gaminv(F,a,lambda)

3.3 例题

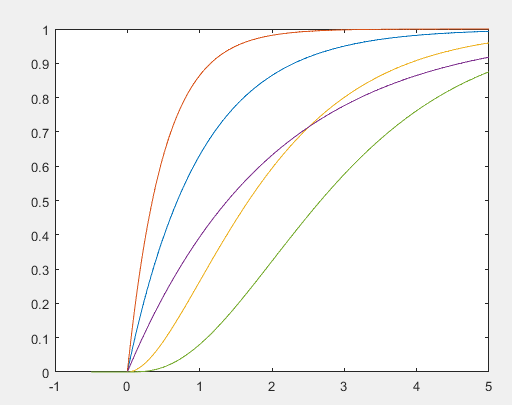
绘制为(1,1),(1,0.5),(2,1),(1,2),(3,1)时伽玛分布的概率密度函数与分布函数曲线。

MATLAB代码：

x=[-0.5:.02:5]';   %图像x轴取值范围
y1=[]; y2=[]; 
a1=[1,1,2,1,3]; 
lam1=[1,0.5,1,2,1];
for i=1:length(a1)
    y1=[y1,gampdf(x,a1(i),lam1(i))]; 
    y2=[y2,gamcdf(x,a1(i),lam1(i))];
end
plot(x,y1), figure; plot(x,y2)

概率密度函数曲线：

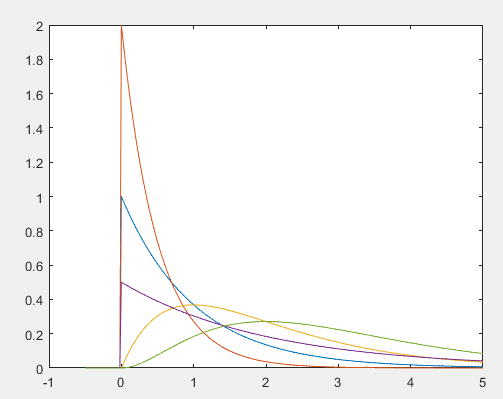
伽马函数的图像趋势一般是先上升后下降。

分布函数曲线：