算法设计与分析复习笔记--第一章

目录

算法与程序

算法复杂性分析

练习题

课堂作业

---

算法与程序

算法的定义：算法是指解决问题的方法和过程。

算法的特性：

1. 确定性：每条指令的意义都是清晰的，无歧义的；如：不允许有诸如“x/0”或“x与1或2相加”之类的运算。
2. 有限性：每条指令的执行次数和执行时间都是有限的；
3. 输入：有零个或多个输入；
4. 输出：至少产生一个量作为输出。

算法要求其执行时间是有限的 (终止性) 。

程序的定义：程序是算法用某种程序设计语言的具体实现。

程序是依赖于程序设计语言的，甚至依赖于计算机结构的。

算法是脱离具体的计算机结构和程序设计语言的。

算法与程序的区别和联系

1. 一个程序不一定满足有限性。例操作系统，只要整个系统不遭破坏，它将永远不会停止，即使没有作业需要处理，它仍处于动态等待中。因此，操作系统不是一个算法。
2. 程序中的指令必须是机器可执行的，而算法中的指令则无此限制。
3. 算法代表了对问题的解，而程序则是算法在计算机上的特定的实现。一个算法若用程序设计语言来描述，则它就是一个程序.

算法描述

算法描述：自然语言，流程图，程序设计语言，伪代码

用各种算法描述方法所描述的同一算法，该算法的功用是一样的，允许在算法的描述和实现方法上有所不同。

问题求解流程

问题表示

设Input和Output是两个集合。一个问题是一个关系R?Input?Output，Input称为问题R的输入集合，Input的每个元素称为R的一个输入，Output称为问题R的输出或结果集合，Output的每个元素称为R的一个结果。

一个算法面向一类问题，而不是仅求解问题的一个或几个实例。

算法的正确性分析

正确的算法：对于每一个输入都最终停止,而且产生正确的输出。

不正确算法： ①不停止(在某个输入上) ②对所有输入都停止，但对某输入产生不正确结果

近似算法 ①对所有输入都停止 ②产生近似正确的解或产生不多的不正确解

算法正确性证明：①证明算法对所有输入都停止②证明对每个输入都产生正确结果

注：调试程序≠程序正确性证明！程序调试只能证明程序有错，不能证明程序无错误!

算法复杂性分析

算法复杂性 = 算法所需要的计算机资源。所需资源量越多则复杂性越高，反之所需资源量越少则复杂性越低。

其中最为重要的是：时间复杂性T(n)；空间复杂性S(n)。其中n是问题的规模（输入大小）。

决定算法复杂性的因素：

(1)求解问题的规模；(2)具体的输入数据；(3)算法本身的设计。

若令N、I、和A分别表示问题的规模、具体的输入和算法本身，则

C = F(N, I, A)或 C = FA(N, I) = F( N, I)

时间复杂性的计算：

时间复杂性T(N, I)的计算为：

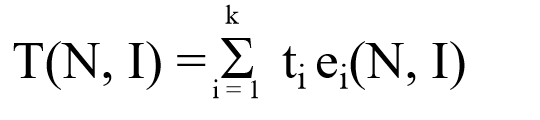
ti为执行抽象计算机的第i种指令一次所需要的时间，这里假定抽象计算机共有k种指令。

ei(N, I)为经过统计后得到的执行抽象计算机的第i种指令的次数。

最坏、最好或平均的情况

最坏情况：Tmax(n) = max{ T(I) | size(I)=n }

最好情况： Tmin(n) = min{ T(I) | size(I)=n }

平均情况： Tavg(n) =

其中I是问题的规模为n的实例，p(I)是实例I出现的概率。

最有实际价值的是最坏情况下的时间复杂性。

用基本运算的次数来度量算法工作量

复杂性分析的简化

令T(N)为表示算法A的复杂性函数，若存在t (N)，使得

那么，就可以用t(N)来代替T(N) ，从而简化复杂性的分析。

用阶来表示复杂性

不必关心t(N)中的常数因子，我们就只需要用t(N)的阶来表示该算法的复杂性。

几个记号

设f(N)、g(N)都是定义在正整数集上的函数。

渐近上界记号O

在大O符号中包含常数因子和低阶项被认为是不好的。应该用大O的最简单形式描述算法的时间复杂性。

注意：

时间复杂度为2n 而不是2n+1

练习题

1.采用顺序查找方法，在长度为n的一维实型数组a[0..n-1]中查找值为x的元素。即从数组的第一个元素开始，逐个与被查值x进行比较。找到后返回1，否则返回0，对应的算法如下：

回答以下问题：分析该算法在等概率情况下成功查找到值为x的元素的最好、最坏和平均时间复杂度。

解：（1）算法的while循环中的if语句是基本语句。a数组中有n个元素，当第一个元素a[0]等于x，此时基本语句仅执行一次，此时呈现最好的情况，即G(n)=O(1)。　　

（2）当a中最后一个元素a[n-1]等于x，此时基本语句执行n次，此时呈现最坏的情况，即W(n)=O(n)。

（3）平均情况：假设查找每个元素的概率相同，则P(a[i])=1/n（0≤i≤n-1），而成功找到a[i]元素时基本语句正好执行i+1次，所以：A(n)=

=O(n)

2.算法复杂度分析

以上三条单个语句的执行次数均为1，该算法段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=Ο(1)。

3.算法复杂度分析

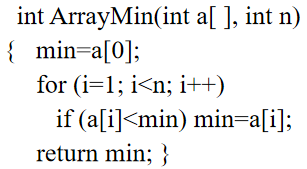
循环体内计算时间*循环次数。如果循环变量与问题规模n有关，则时间复杂度一般为O(n)。

该算法段的时间复杂度为T(n)=Ο(n2)。

当有若干个嵌套循环语句时，算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的执行次数决定的。

4.

该算法时间复杂度为O(n3 )

非递归算法的基本法则：

1. 顺序语句： 各语句计算时间相加；
2. for / while 循环：循环体内计算时间*循环次数；
3. 嵌套循环： 最深层循环体内计算时间*所有循环次数；
4. if-else语句： if语句计算时间和else语句计算时间的较大者。

算法复杂性的一般表示形式

分治法(Divide and Conquer)动态规划法(Dynamic Programming)贪心法(Greedy)回溯法(Backtracking)分支界限法(Branch and Bound)这些算法中都使用了递归(Recursion)。

伪代码

伪代码是自然语言和高级程序设计语言的混合物，它描述数据结构或算法的主要实现。然而，由于伪代码依赖于自然语言，因此实际上伪代码语言没有精确的定义。

编写伪代码时，切忌是为读者而不是为计算机编写的。因此，应力图传达一些高级思想，而不是低级的实现细节。同时，对于重要步骤，不能一笔带过。

就像人类的许多交流形式，找到合适的平衡是一项重要的技能，大家可以通过实践逐步改进。

课堂作业

O(n)=n!

1!*1+2!*2+3!*3+4!*4+5!*5+...+n!*n

n!*n=n!*(n+1-1)=n!*(n+1)-n!=(n+1)!-n!

1!*1+2!*2+3!*3+4!*4+5!*5+...+n!*n
=2!-1!+3!-2!+4!-3!+5!-4!+...+(n+1)!-n!=(n+1)!-1

所以：O(n)=n! ！！！！！！！！！！！！！！！！！