SM4加密算法的侧信道攻击实现
SM4 算法有多个位置存在泄漏点,如下图所示:
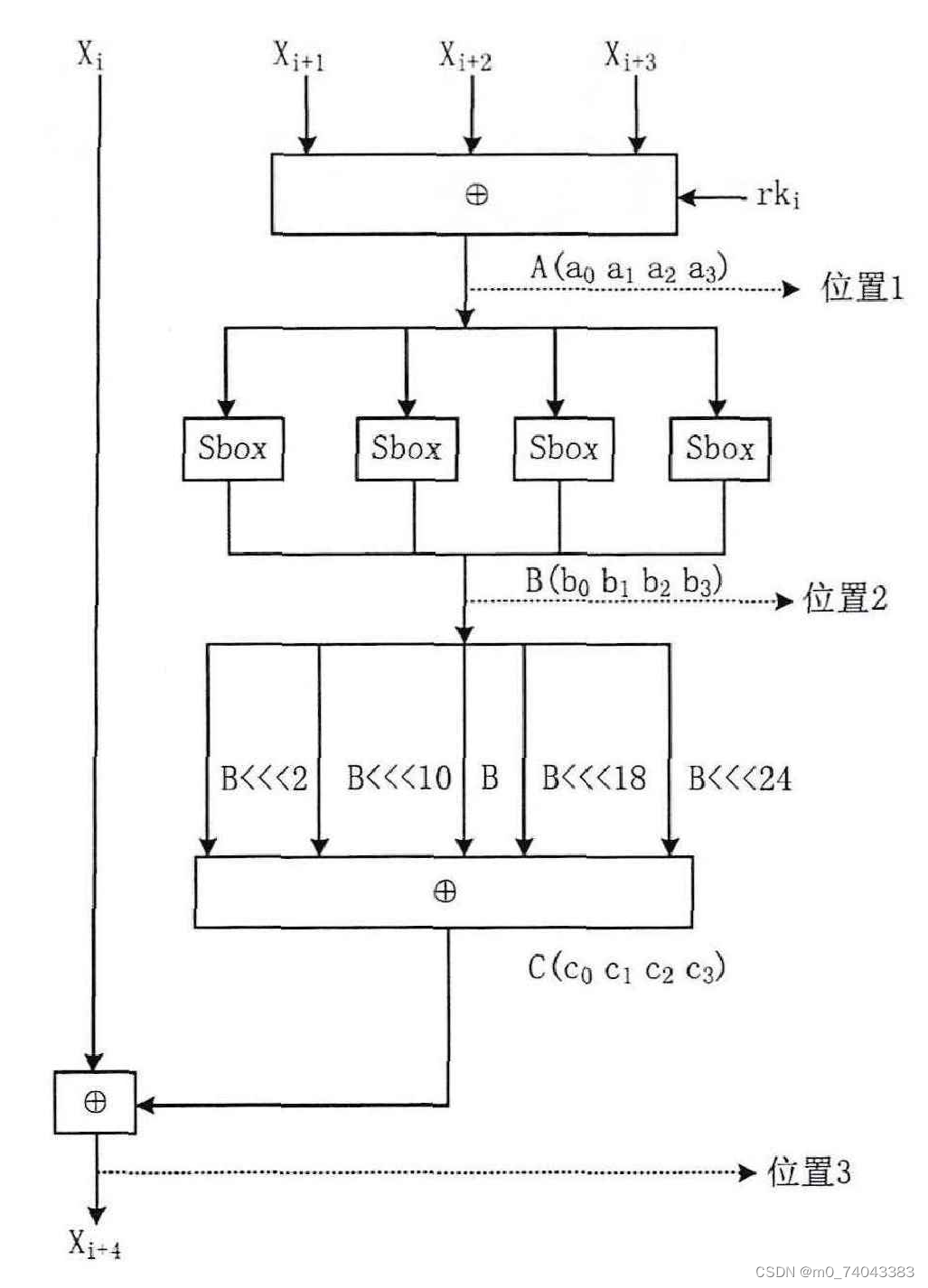
在位置1和2,可以逐个字节攻击密钥,因为密钥和中间结果之间没有扩散,这时通常取Sbox的输出作为攻击点,因为在位置2处的功耗是大于位置1的,但是在FPGA硬件电路中,Sbox产生的功耗相对于状态寄存器来说小得多,有文章中的数据显示,如果攻击点在Sbox处,至少需要采集270000条功率曲线才可以破解出密钥。在实际密码电路中,产生功耗的寄存器出现在位置3,因为SM4算法的移位操作,密钥和明文高度混淆,直接攻击需要
2
32
2^{32}
232次穷举尝试,如果选择随机明文,则在位置3中不可能进行攻击。因为选择位置3作为攻击点时,应该使用选择特定的明文方法来获得密钥。这与破解AES密钥是不同的,因为在AES的每轮的状态寄存器中,最后一步是轮密钥加操作,状态寄存器的每个字节的数据只与其对应的密钥字节有相关性,可以使用正常的随机明文作为输入来攻击。
对于SM4算法而言,使用选择特定的明文方法如下:
(1)以第一轮攻击为例,第一轮密钥为
r
k
0
rk_0
rk0?,记
r
k
0
=
(
r
k
0
,
0
,
r
k
0
,
1
,
r
k
0
,
2
,
r
k
0
,
3
)
rk_0 = (rk_{0,0}, rk_{0,1},rk_{0,2},rk_{0,3})
rk0?=(rk0,0?,rk0,1?,rk0,2?,rk0,3?)。
(2)选择明文
(
X
0
,
X
1
,
X
2
,
X
3
)
=
(
00000000
h
,
00000000
h
,
00000000
h
,
X
X
000000
h
)
(X_0,X_1,X_2,X_3)=(00000000h, 00000000h, 00000000h,XX000000h)
(X0?,X1?,X2?,X3?)=(00000000h,00000000h,00000000h,XX000000h),其中
X
X
XX
XX表示一个字节的随机数据。根据SM4算法步骤,经过Sbox替换后,输出的值为:
B
=
(
S
b
o
x
(
X
X
⊕
r
k
0
,
0
)
,
S
b
o
x
(
r
k
0
,
1
)
,
S
b
o
x
(
r
k
0
,
2
)
,
S
b
o
x
(
r
k
0
,
3
)
)
B = (Sbox(XX \oplus rk_{0,0}), Sbox(rk_{0,1}), Sbox(rk_{0,2}), Sbox(rk_{0,3}))
B=(Sbox(XX⊕rk0,0?),Sbox(rk0,1?),Sbox(rk0,2?),Sbox(rk0,3?))
从这看出,只有 32bits的
b
0
b_0
b0? 是变量,其他
b
1
,
b
2
,
b
3
b_1, b_2,b_3
b1?,b2?,b3?都是常量,为了便于表述,把Sbox输出
B
B
B以及移位的结果在下表中进行推导,表中字母
X
X
X表示1bit变量,其他字母表示1bit固定常量。
| 移位操作 | 32bit寄存器中的值 |
|---|---|
| B = ( b 0 , b 1 , b 2 , b 3 ) B=(b_0,b_1,b_2,b_3) B=(b0?,b1?,b2?,b3?) | XXXXXXXX ABCDEFGH IJKLMNOP QRSTUVWY |
| 移位2比特 | XXXXXXAB CDEFGHIJ KLMNOPQR STUVWYXX |
| 移位10bit | CDEFGHIJ KLMNOPQR STUVWYXX XXXXXXAB |
| 移位18 bits | KLMNOPQR STUVWYXX XXXXXXAB CDEFGHIJ |
| 移位24bits | QRSTUVWY XXXXXXXX ABCDEFGH IJKLMNOP |
(3)经过线性位移后,状态寄存器的值为:
C
=
B
⊕
(
B
<
<
<
2
)
⊕
(
B
<
<
<
10
)
⊕
(
B
<
<
<
18
)
⊕
(
B
<
<
<
24
)
C=B \oplus(B <<< 2) \oplus (B <<< 10) \oplus (B <<< 18) \oplus (B <<< 24)
C=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)
其中
c
0
c_0
c0? 表达式如下:
c
0
=
b
0
⊕
(
b
0
<
<
<
2
)
⊕
m
a
s
k
c_0 = b_0 \oplus (b_0 <<< 2) \oplus mask
c0?=b0?⊕(b0?<<<2)⊕mask
mask 是一个与后3个字节的子密钥相关的未知的8 bits 常量。根据表达式可以看出
c
0
c_0
c0? 与轮密钥的第一个字节
r
k
0
,
0
rk_{0,0}
rk0,0?具有很强的相关性,根据功耗攻击原理,可以恢复出
r
k
0
,
0
rk_{0,0}
rk0,0?。同理,如果选择明文:
(
X
0
,
X
1
,
X
2
,
X
3
)
=
(
00000000
h
,
00000000
h
,
00000000
h
,
00
X
X
0000
h
)
(X_0,X_1,X_2,X_3) = (00000000h, 00000000h, 00000000h, 00XX0000h)
(X0?,X1?,X2?,X3?)=(00000000h,00000000h,00000000h,00XX0000h)可以恢复出
r
k
0
,
1
rk_{0,1}
rk0,1?,依次按字节恢复出轮密钥,然后依据第1-4轮的轮密钥通过密钥扩展算法反推出加密的原始密钥。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- FPGA引脚物理电平(内部资源,Select IO)-认知2
- 神舟飞船科普网站的设计与实现(JSP+java+springmvc+mysql+MyBatis)
- 不留遗憾 | 三年浇灌,终是开出了花儿
- 【XR806开发板试用】留言板功能开发
- 【lesson18】MySQL内置函数(1)日期函数和字符串函数
- 软信天成:选择和部署主数据管理(MDM)的十大关键要求(下)
- 基于长短期神经网络LSTM的路径追踪
- XV7021BB陀螺仪传感器
- Python游戏开发实战:经典游戏制作教程
- docker--Prometheus、Grafana、node_exporter的安装配置及Springboot集成Prometheus示例