B-TREE(B-树)

B-TREE

B-tree 又叫平衡多路查找树。一棵 m 阶的 B-tree (m 叉树)的特性如下（其中 ceil(x)是一个取上限的函数）：

1. 树中每个结点至多有 m 个孩子；

2. 除根结点和叶子结点外，其它每个结点至少有有 ceil(m / 2)个孩子；

3. 若根结点不是叶子结点，则至少有 2 个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；

4. 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部结点或查询失败的结点，实际上这些结点不存在，指向这些结点的指针都为 null)；

5. 每个非终端结点中包含有 n 个关键字信息： (n，P0，K1，P1，K2，P2，…，Kn，Pn)。其中：

a) Ki (i=1…n)为关键字，且关键字按顺序排序 K(i-1)< Ki。

b) Pi 为指向子树根的接点，且指针 P(i-1)指向子树种所有结点的关键字均小于 Ki，但都大于 K(i-1)。

c) 关键字的个数 n 必须满足： ceil(m / 2)-1 <= n <= m-1

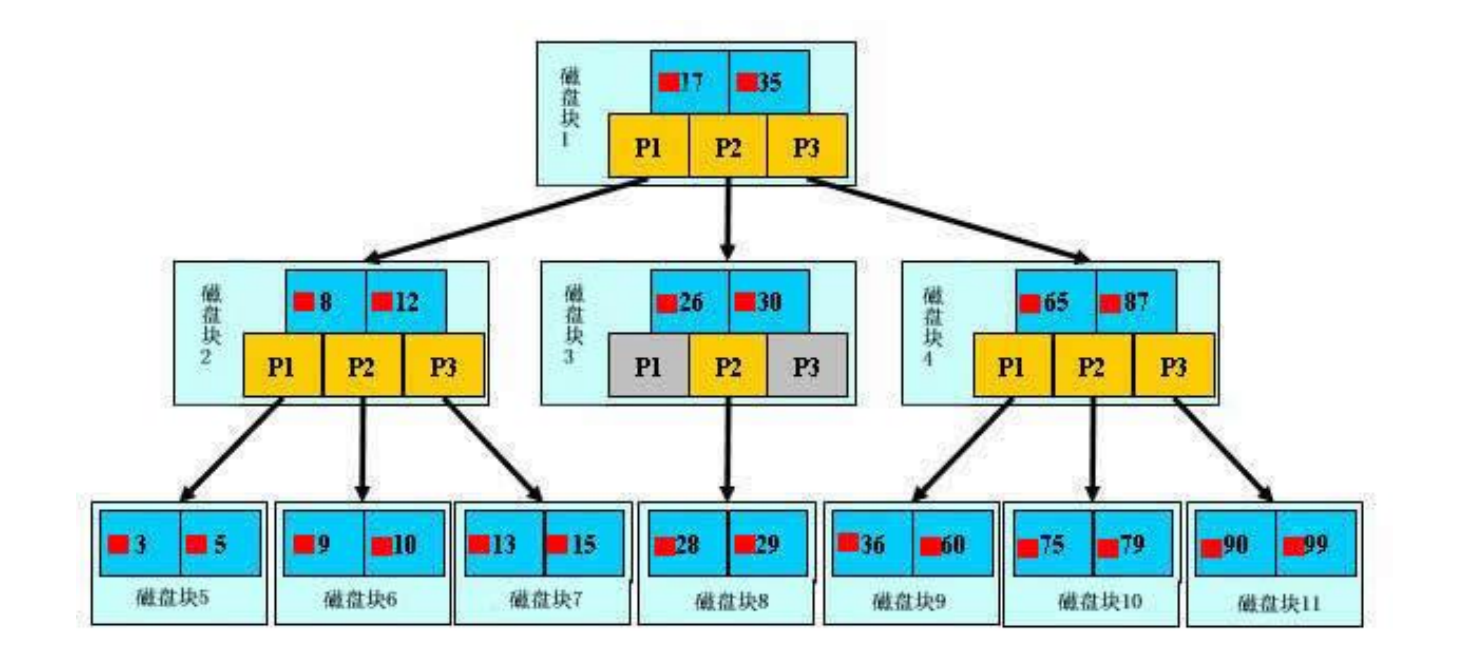
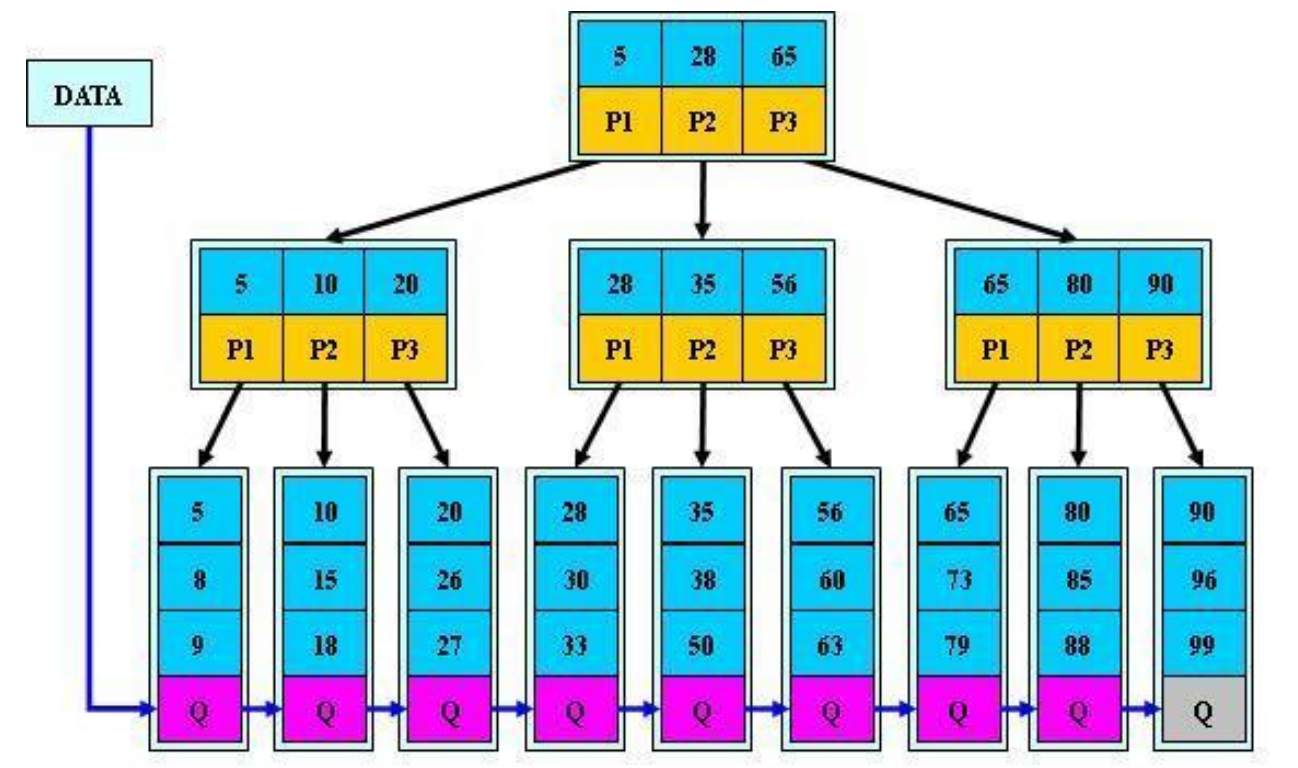
一棵 m 阶的 B+tree 和 m 阶的 B-tree 的差异在于：

1.有 n 棵子树的结点中含有 n 个关键字； (B-tree 是 n 棵子树有 n-1 个关键字)

2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (B-tree 的叶子节点并没有包括全部需要查找的信息)

3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。

(B-tree 的非终节点也包含需要查找的有效信息)