蓝桥杯软件类考点2：排序

一、前提声明

1、什么是冒泡排序

????????冒泡排序是一种简单的排序算法，它的时间复杂度为O(n^2),n为列表长度，它重复地遍历要排序的列表，比较相邻的两个元素，并依次交换顺序，直到整个列表按照指定顺序排序。它的名字来源于排序过程中较小的元素像“气泡”一样逐步“浮”到列表的顶端。

????????冒泡排序的基本思想是每次比较相邻的两个元素，如果它们的顺序不符合预期（升序或降序），则交换它们的位置。通过多次遍历，把最大（或最小）的元素“冒泡”到顶端（或底端），从而完成排序。

2、什么是选择排序

????????选择排序是一种简单的排序算法，它的基本思想是每次在未排序的部分找到最小（或最大）的元素，然后将其放到已排序部分的末尾。它与冒泡排序类似，都属于基于比较的排序算法，但选择排序不同于冒泡排序的地方在于它不是交换相邻元素，而是选择合适的元素放在已排序的部分。

选择排序的步骤如下：

1、在未排序序列中找到最小元素，并将其放置在序列的起始位置（如果要进行升序排序，则是放在已排序部分的末尾）。
2、从剩余未排序的部分中继续寻找最小元素，并将其放到已排序部分的末尾。
3、重复上述步骤，直到所有元素都排序完成。
????????选择排序的时间复杂度为O(n^2)，其中n是要排序的元素个数。尽管选择排序是一种简单的算法，但在实际应用中，它相对效率较低，尤其在处理大量数据时。

3、什么是插入排序

????????插入排序是一种简单直观的排序算法，它的基本思想是将一个元素插入到已经排序好的部分中，从而逐步扩大已排序部分，直到所有元素都被排序完成。

插入排序的步骤如下：

1、将第一个元素视为已排序部分。
2、从第二个元素开始，依次将元素插入到已排序的部分中，保持已排序部分的顺序性。插入时，将当前元素与已排序部分中的元素逐个比较，找到合适的位置插入。
3、重复上述步骤，直到所有元素都被插入到已排序部分。
????????插入排序的时间复杂度为O(n^2)，其中n是要排序的元素个数。尽管插入排序相对于其他高级的排序算法可能效率较低，但对于小型数据集或者是部分已排序的列表，它的性能可能更好

4、什么是归并排序

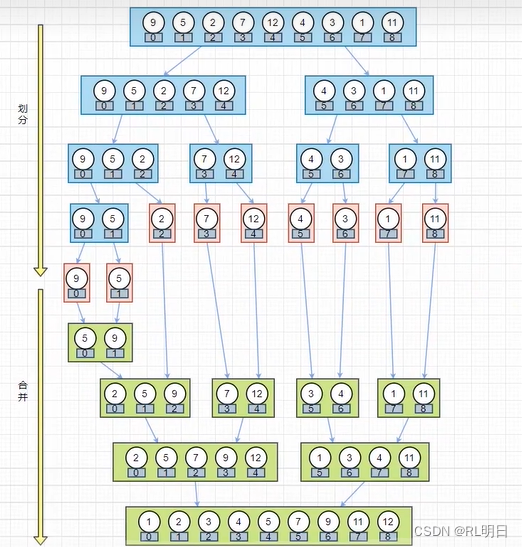
????????归并排序是一种分治法（Divide and Conquer）的经典排序算法，其基本思想是将待排序的序列划分为若干个子序列，分别进行排序，然后再合并这些子序列，最终得到一个完整有序的序列。

归并排序的步骤如下：

1、分解：将原始序列分解为更小的序列，直到每个子序列只有一个元素为止。
2、合并：将两个已排序的子序列合并成一个有序序列。合并时比较两个子序列的第一个元素，将较小（或较大）的元素放入新的序列中，并继续比较下一个元素，直到其中一个子序列被完全合并。
3、递归：递归地将子序列两两合并，直到最终形成一个完整有序序列。
????????归并排序的时间复杂度是O(nlogn)，其中n是要排序的元素个数。它的优点在于稳定且效率高，特别适合对链表或数组等结构进行排序。然而，归并排序需要额外的存储空间来暂存合并过程中的元素，因此在处理大型数据集时可能需要更多的内存。

5、什么是快速排序

????????快速排序是一种高效的排序算法，它采用分治法的思想，通过递归地将列表分割成较小的子列表来实现排序。快速排序的基本思想是选择一个基准值，然后将列表中小于基准值的元素放在基准值的左边，大于基准值的元素放在右边，最终达到排序的目的。

快速排序的步骤如下：

1、选择基准值：从列表中选择一个基准值（通常是列表的第一个元素、最后一个元素或中间元素）。
2、分割：将列表中小于基准值的元素放在基准值的左边，大于基准值的元素放在右边。在这个过程中，基准值的位置也确定了。
3、递归：对分割后的两个子列表重复上述步骤，直到每个子列表只有一个元素为止。
????????快速排序的时间复杂度平均为O(nlogn)，其中n是要排序的元素个数。尽管在最坏情况下可能达到O(n^2)，但在大多数情况下，快速排序仍然是一种高效的排序算法，尤其适用于处理大量数据集。

通过以下链接快速了解:【三分钟学会快速排序】 https://www.bilibili.com/video/BV1j841197rQ/?share_source=copy_web&vd_source=307838fdbdb0dab7d7988f7b676ed038

6、什么是桶排序

桶排序是一种排序算法，它的基本思想是将待排序的元素分到有限数量的桶中，然后对每个桶中的元素进行排序，最后按照桶的顺序依次将各个桶中的元素合并起来。

桶排序的步骤如下：

1、分桶：将待排序的元素按照一定的规则分到有限数量的桶中。这个分桶的规则可以是简单的取余数、映射到桶的索引等。
2、对每个桶排序：对每个桶中的元素进行排序。可以选择使用其他排序算法，比如插入排序或者快速排序。
3、合并：按照桶的顺序依次将各个桶中的元素合并起来。
????????桶排序的时间复杂度取决于对每个桶中元素的排序算法和分桶策略。如果分桶合理，并且每个桶中的元素数量均匀，桶排序的时间复杂度可以达到线性时间O(n)，其中n是要排序的元素个数。桶排序通常适用于待排序的元素均匀分布在某个范围内的情况。

7、什么是堆排序

????????堆排序是一种基于二叉堆数据结构的排序算法，它利用堆的性质进行排序。堆是一个特殊的树形数据结构，它满足堆属性：对于每个节点i，其父节点i/2的值不大于节点i的值。在堆中，根节点通常是最大值（最大堆）或最小值（最小堆）。

堆排序的基本思想是：

1、构建初始堆：将待排序的元素构建成一个堆。
2、交换：将堆顶元素（最大值或最小值）与堆的最后一个元素交换位置，然后对剩余的部分重新调整为堆。
3、重复步骤2，直到堆中只有一个元素。
????????堆排序的时间复杂度为O(n log n)，其中n是要排序的元素个数。它是一种不稳定的排序算法，因为在堆的调整过程中，相同值的元素可能会交换位置。堆排序在大数据集上表现较好，且不需要额外的存储空间，因为它是原地排序算法。

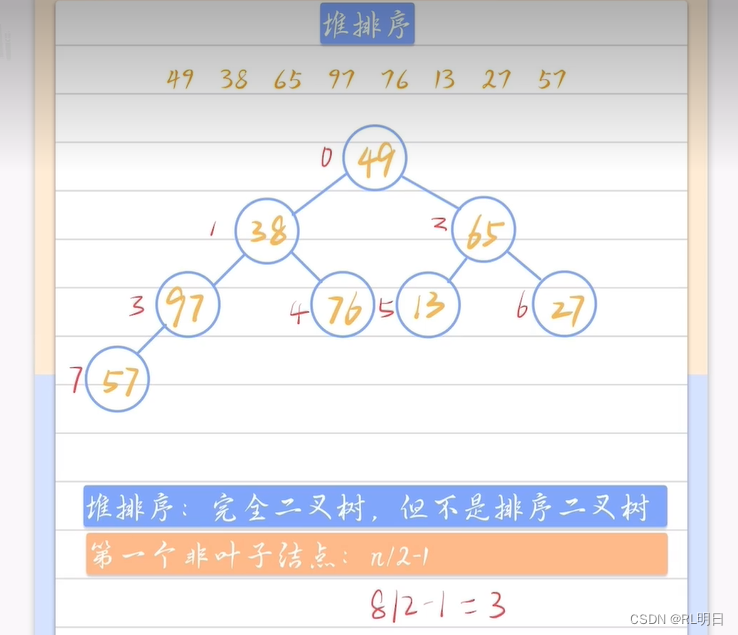
详细请观看以下链接:【数据结构——堆排序】 https://www.bilibili.com/video/BV1aj411M71h/?share_source=copy_web&vd_source=307838fdbdb0dab7d7988f7b676ed038

8、什么是基数排序

????????基数排序是一种非比较型的排序算法，它将待排序的元素按照位数切割成不同的数字，然后按照每个位数进行排序。基数排序可以分为 LSD（最低位优先）和 MSD（最高位优先）两种方式。

LSD 基数排序（最低位优先）：

1、从最右边的位数开始，按照每个位数进行排序。
2、排序完成后，将元素按照当前位数的顺序重新排列。
3、重复以上步骤，直到最高位数。

MSD 基数排序（最高位优先）：

1、从最左边的位数开始，按照每个位数进行排序。
2、排序完成后，将元素按照当前位数的顺序重新排列。
3、递归地对每个子序列进行排序，直到排序完成。
????????基数排序适用于整数或字符串等数据类型，而不适用于包含负数的整数。它的时间复杂度是 O(nk)，其中 n 是元素个数，k 是元素的最大位数。基数排序的优点在于稳定、非比较型，对于大量数据和位数相对较小的情况，它可以是一种有效的排序方法。

详细请观看以下链接:【基数排序】 https://www.bilibili.com/video/BV1YM4y1A7wi/?share_source=copy_web&vd_source=307838fdbdb0dab7d7988f7b676ed038

二、试题练习

1、冒泡排序

排序前：70 80 31 37 10 1 48 60 33 80

def data_sort(arr):
    n = len(arr)
    for i in range(n-1): #n个数据，执行n-1次外层循环
        for j in range(n-i-1):
            if arr[j] > arr[j+1]:
                arr[j],arr[j+1] = arr[j+1],arr[j]# 如果顺序不对，交换位置

if __name__ == '__main__':
    arr = [70,80,31,37,10,1,48,60,33,80]
    print(f'排序前:',arr)
    data_sort(arr)
    print(f'排序后:',arr)

2、选择排序

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_idx = i   #假设当前索引为最小索引
        # 在未排序部分中找到最小元素的索引
        for j in range(i+1,n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        # 将找到的最小元素与当前位置交换
        arr[i],arr[min_idx] = arr[min_idx],arr[i]

if __name__ == '__main__':
    arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
    print(f'排序前:', arr)
    selection_sort(arr)
    print(f'排序后:', arr)

3、插入排序

def insection_sort(arr):
    n = len(arr)

    for i in range(1,n):
        current = arr[i] #保存当前插入的值
        j = i - 1  # 已排序部分的最后一个元素的索引

        while j >= 0 and arr[j]>current:
            arr[j+1] = arr[j] # 向右移动元素
            j -= 1  #逐一与已排序序列比较

        arr[j+1] = current  # 将当前元素插入合适的位置

if __name__ == '__main__':
    arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
    print(f'排序前:',arr)
    insection_sort(arr)
    print(f'排序后:',arr)

4、归并排序

def merge_sort(arr):
    if 1 < len(arr):
        mid = len(arr)//2 #计算中间索引
        left_half = arr[:mid] #二分法分割数列
        right_half = arr[mid:]

        merge_sort(left_half)  #递归调用，直至分成单个元素
        merge_sort(right_half)

        #归并过程
        i = j = k = 0

        #两者相比，排小的元素
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                arr[k] = left_half[i]
                i += 1
            else:
                arr[k] = right_half[j]
                j += 1
            k += 1

        # 两者相比，排大的元素
        while i < len(left_half):
            arr[k] = left_half[i]
            i += 1
            k += 1

        while j < len(right_half):
            arr[k] = right_half[j]
            j += 1
            k += 1

if __name__ == '__main__':
    arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
    print(f'排序前:', arr)
    merge_sort(arr)
    print(f'排序后:',arr)

5、快速排序

'''
return quick_sort(left) + [pivot] + quick_sort(right) 是快速排序算法中递归调用的一部分，它负责将左右两个子列表排序后再合并起来。
让我解释它的执行顺序：
1、quick_sort(left): 这是对左子列表进行递归调用，对左边部分的子列表 left 进行排序。这一步会重复快速排序算法的整个流程：选择基准值、分割列表、
递归排序左右子列表，直到左子列表长度为1或为空。
2、quick_sort(right): 同样的方式对右子列表进行递归调用，对右边部分的子列表 right 进行排序。
3、+ [pivot] +: 基准值 pivot 是一个单独的元素（一个列表），它被放在左右子列表排序后的中间位置。在合并的过程中，它会和左右子列表的排序结果连接起来。
最终，quick_sort(left) 和 quick_sort(right) 递归调用将返回排序好的左右子列表。这两个排序好的子列表与基准值 pivot
以及它们之间的连接（+ [pivot] +）一起组成了整个列表的排序结果。
这个过程是递归的，每次递归都会对左右两个子列表进行排序，直到所有的子列表长度为1或为空，然后再进行合并操作，最终得到完整的排序列表。
'''

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0] #选择第一个元素为基准值
        left = [x for x in arr[1:] if x <= pivot] #小于等于基准值的放左边
        right = [x for x in arr[1:] if x > pivot] #大于基准值的放右边

        return quick_sort(left) + [pivot] + quick_sort(right)


if __name__ == '__main__':
    arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
    print(f'排序前:', arr)
    quick_sort(arr)
    print(f'排序后:',arr)

6、桶排序

'''
[_ for _ in range(bucket_count)]：使用列表推导式创建一个包含 bucket_count 个元素的列表，这些元素取值为 _，
但实际上并不会被使用。这种写法是为了简单地生成一个包含指定数量元素的列表。
'''

def bucket_sort(arr):
    #确定最大最小值，用来确定范围，直至于找到合适的桶数
    max_value = max(arr)
    min_value = min(arr)

    #计算了每个桶的范围，以便将元素放入相应的桶中
    bucket_range = (max_value - min_value) // len(arr) + 1
    #用范围确定桶数
    bucket_count = (max_value - min_value) // bucket_range + 1

    #初始化桶
    bucket = [[] for _ in range(bucket_count)]

    #将元素分配到桶中
    for num in arr:
        index = (num - min_value) // bucket_range
        bucket[index].append(num)

    # 对每个桶中的元素进行排序
    for i in range(bucket_count):
        bucket[i].sort()

    # 合并各个桶中的元素
    sort_arr = []
    for i in bucket:
        sort_arr.extend(bucket)
    
    return sort_arr

if __name__ == '__main__':
    arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
    print(f'排序前:', arr)
    bucket_sort(arr)
    print(f'排序后:',arr)

7、堆排序

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    # 检查左子节点是否比根节点大
    if left < n and arr[left] > arr[largest]:
        largest = left

    # 检查右子节点是否比根节点大
    if right < n and arr[right] > arr[largest]:
        largest = right

    # 如果根节点不是最大值，交换根节点和最大值
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        # 递归调整子堆
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # 构建初始最大堆
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 交换堆顶元素和堆的最后一个元素，然后调整堆
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

# 给定列表
arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
print("排序前:", arr)

# 调用堆排序函数
heap_sort(arr)

print("排序后:", arr)

8、基数排序

def radix_sort(arr):
    # 找到数组中最大的数，以确定最大位数
    max_num = max(arr)
    exp = 1

    # LSD 基数排序
    while max_num // exp > 0:
        counting_sort(arr, exp)
        exp *= 10

def counting_sort(arr, exp):
    n = len(arr)
    output = [0] * n
    count = [0] * 10

    # 统计每个桶中的元素个数
    for i in range(n):
        index = arr[i] // exp
        count[index % 10] += 1

    # 将 count 转换为每个桶的结束索引
    for i in range(1, 10):
        count[i] += count[i - 1]

    # 根据 count 将元素放入正确的位置
    i = n - 1
    while i >= 0:
        index = arr[i] // exp
        output[count[index % 10] - 1] = arr[i]
        count[index % 10] -= 1
        i -= 1

    # 将排序好的数组复制回原数组
    for i in range(n):
        arr[i] = output[i]

# 给定列表
arr = [70, 80, 31, 37, 10, 1, 48, 60, 33, 80]
print("排序前:", arr)

# 调用基数排序函数
radix_sort(arr)

print("排序后:", arr)