梯度下降算法实现原理
什么是梯度
在了解梯度之前,我们先了解一下导数:
用于描述曲线变换快慢的一个量,在几何意义上表示为函数的斜率,数学定义为:
f ′ ( x ) = lim ? △ x → 0 f ( x + △ x ) ? f ( x ) △ x f'(x) = \lim_{{△x \to 0}} \frac{{f(x + △x) - f(x)}}{△x} f′(x)=△x→0lim?△xf(x+△x)?f(x)?
- 当导数大于0时候,则单调递增,当导数小于0时候,则单调递减,所以,我们可以根据导数值,来求取函数的最值.

那如果是多元函数,我们怎么求最值呢?答案是分别对多元变量求取 偏导数,即对哪个变量求导,就把其余变量看做常数,以f(x,y)为例,数学定义对x和对y求偏导为:
?
f
?
x
=
lim
?
△
x
→
0
f
(
x
+
△
x
,
y
)
?
f
(
x
,
y
)
△
x
\frac{\partial f}{\partial x} = \lim_{{△x \to 0}} \frac{{f(x + △x, y) - f(x, y)}}{△x}
?x?f?=△x→0lim?△xf(x+△x,y)?f(x,y)?
? f ? y = lim ? △ y → 0 f ( x , y + △ y ) ? f ( x , y ) △ y \frac{\partial f}{\partial y} = \lim_{{△y \to 0}} \frac{{f(x, y + △y) - f(x, y)}}{△y} ?y?f?=△y→0lim?△yf(x,y+△y)?f(x,y)?
而梯度就是我们的多元函数的偏导向量,梯度向量的方向是函数值变化率最大的方向, 简单理解就是对于函数某个特定点,它的梯度就表示从该点出发,函数值变化最迅猛的方向。:
?
f
(
x
,
y
)
=
(
?
f
?
x
,
?
f
?
x
)
\nabla f(x, y) = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial x})
?f(x,y)=(?x?f?,?x?f?)
例如我们的

f ( x , y ) = x 2 + y 2 f(x, y) = x^2 + y^2 f(x,y)=x2+y2
则
?
f
(
x
,
y
)
=
(
?
f
?
x
,
?
f
?
x
)
=
(
2
x
,
2
y
)
\nabla f(x, y) = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial x}) =(2x,2y)
?f(x,y)=(?x?f?,?x?f?)=(2x,2y)

我们可以清晰的看到,在点(1, 1)位置,函数值为1^2 + 1^2=2。
如果按照向量(-1, 0)的方向移动一个1个单位,到达(0, 1), 函数值为0^2+1^2=1, 比f(1, 1) 减小1。
换另一 个方向,按照向量(1, 0)的方向移动1到达(2, 1) 函数值为2^2+1^2=5 比f(1, 1) 增加3.
但是按照梯度方向(2, 2) 移动1,大约到达(1.7, 1.7),函数值为1.7^2 + 1.7^2 = 5.78 比f(1, 1) 增加3.78。
所以按照梯度方向移动,函数增加最迅猛。
梯度下降算法(通过迭代解决目标函数最小值)
我们用一个例子进行引入该算法:
目前有一组关于房屋面积和价格关系的数据,我们想用该组数据的大致关系,制作一个数学模型,用于预测其余面积可能的价格.
根据图中点图,我们可能会容易想到用模型
y
=
w
x
+
b
y = wx + b
y=wx+b
但是这样就有个问题了,k和b到底应该怎样设置呢?不同的k和b会有不一样的拟合效果:

根据肉眼,我们可能觉得第2,3,4幅图效果比较好,但是后面的三幅图又怎么比较呢?
我们这里采取真实值和模型的差值平方均值的和 最小 (一般是均方误差损失函数(MSE)来表示)表示:

其公式为:
MSE
=
1
n
∑
i
=
1
n
(
y
^
i
?
y
i
)
2
,
其中
n
是样本数量
,
y
i
是实际值
,
y
i
^
是预测值
\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2 ,其中n是样本数量,y_i是实际值,\hat{y_i}是预测值
MSE=n1?i=1∑n?(y^?i??yi?)2,其中n是样本数量,yi?是实际值,yi?^?是预测值
如果我们把y = kx +b带入公式MSE中,就会得到
j
(
w
,
b
)
=
1
n
∑
i
=
1
n
(
w
x
i
+
b
?
y
i
)
2
,
x
i
和
y
i
都是我们已知的样本实际值
,
可以当成常数
j(w,b) = \frac{1}{n} \sum_{i=1}^{n} (wx_i + b - y_i)^2,x_i和y_i都是我们已知的样本实际值,可以当成常数
j(w,b)=n1?i=1∑n?(wxi?+b?yi?)2,xi?和yi?都是我们已知的样本实际值,可以当成常数
所以,很明显,只要我们使函数j(w,b)的值最小,那么就可以获取到最适合的预测模型,而这我们就可以使用梯度下降算法了
- 即分别对损失函数的自变量求偏导数
- 然后分别对参数利用
数学公式更新到最合适的值(别问我公式怎么来的,网上有推导过程) - 最后迭代好后的参数,就可以构成我们想要的最合适的模型
y = wx + b
以损失函数j(w,b)为例:
- 分别计算梯度(偏导数)为:
? j ? w = 1 n ∑ i = 1 n 2 ( w x i + b ? y i ) ? x i \frac{\partial j}{\partial w} = \frac{1}{n} \sum_{i=1}^{n} 2(wx_i + b - y_i) \cdot x_i ?w?j?=n1?i=1∑n?2(wxi?+b?yi?)?xi?
? j ? b = 1 n ∑ i = 1 n 2 ( w x i + b ? y i ) \frac{\partial j}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} 2(wx_i + b - y_i) ?b?j?=n1?i=1∑n?2(wxi?+b?yi?)
- 然后分别对参数进行更新
w i + 1 = w i + ( ? a ? j ? w ) = w i ? a ? j ? w w_{i+1} =w_i +(-a\frac{\partial j}{\partial w}) = w_i-a\frac{\partial j}{\partial w} wi+1?=wi?+(?a?w?j?)=wi??a?w?j?
b i + 1 = b i + ( ? a ? j ? b ) = b i ? a ? j ? b b_{i+1} =b_i +(-a\frac{\partial j}{\partial b}) = b_i-a\frac{\partial j}{\partial b} bi+1?=bi?+(?a?b?j?)=bi??a?b?j?
这个a是学习率,也叫步进值,其值设置一般为0.1或者0.01,如下图:

- 我们对更新完毕后的最终参数带入模型就是我们要的最合适拟合线
y = w i x + b i y = w_ix + b_i y=wi?x+bi?
代码实现
就以上面那个例子为例,有一组类线性数据,请你利用 梯度下降算法 思想进行模拟得到合适线
import random
import numpy as np
from matplotlib import pyplot as plt
# 1. 提供的真实的波动数据x和y集,可以理解为房屋面积和价格真实值
_x = [x/100 for x in range(100)]
_y = [4*x+5+random.random() for x in _x]
# 2. 随机给定 y = wx+b 模型中的w 和 b一个初始值,以方便后续参数更新迭代到合适值
w = random.random()
b = random.random()
for i in range(1000):
for x, y in zip(_x, _y):
# 3. 给定预测模型 h = w*x+b
h = w * x + b
# 4. 确定均方误差函数(损失函数)
loss = (h - y) ** 2 # 本质是loss = (w*x+b - y)**2,我这里只是为了方便演示和计算,该函数简化了
# 5. 对 w, b 求偏导,同时给定学习率(步长)
dw = 2 * (h - y) * x
db = 2 * (h - y)
learn_ratio = 0.1
# 6. 参数迭代
w = w - learn_ratio * dw # 本质上是 w + -(learn_ratio*dw)
b = b - learn_ratio * db
# 然后把第三步到第六步代码 用准备的真实数据 去迭代更新修正(即放到for x,y in zip(_x,_y)循环
# 由于物理限制,我们的预测模型是根据每一个真实点 顺序校验 一遍!!!! 得来的,这不够,所以我们在外面继续套个循环迭代校验1000次以上,这样更准确
# 这里进行可视化一下,让我们更加直观理解回归
# 如果想看到动态模拟的过程,下面这些代码就全部和第二个for循环对齐,不过就可能有点浪费时间了
plt.ion()
plt.plot(_x,_y,'.') # 真实值点图
plt.plot(_x,[w*ele+b for ele in _x]) # 绘制预测模型图
plt.pause(0.01)
plt.cla() # 清屏
plt.show()
模拟效果(黄线是模型,点是真实值):
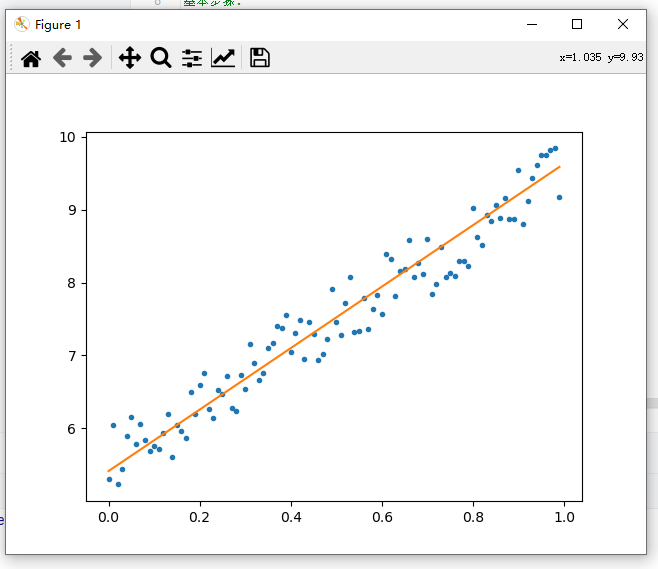
如果我们有时候不知道用什么模型去拟合散乱数据,可以用泰勒展开式(或者多项式)模型进行拟合,公式为:
f
(
x
)
=
f
(
a
)
+
f
′
(
a
)
(
x
?
a
)
+
f
′
′
(
a
)
2
!
(
x
?
a
)
2
+
f
′
′
′
(
a
)
3
!
(
x
?
a
)
3
+
…
,
(
泰勒展开式
)
f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \ldots ,(泰勒展开式)
f(x)=f(a)+f′(a)(x?a)+2!f′′(a)?(x?a)2+3!f′′′(a)?(x?a)3+…,(泰勒展开式)
f ( x ) = a n x n + a n ? 1 x n ? 1 + … + a 1 x + a 0 , ( 多项式 ) f(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0,(多项式) f(x)=an?xn+an?1?xn?1+…+a1?x+a0?,(多项式)
其中常数和系数就是参数,可以自己任意选择参数数量
拓展:
给定一组真实数据:
_x = [ele / 100 for ele in range(100)]
_y = [3 * np.sin(5 * ele) + ele * 2 + 10 + random.random() for ele in _x]
请你利用多项式 梯度下降算法拟合
代码:
import random
import numpy as np
from matplotlib import pyplot as plt
_x = [ele / 100 for ele in range(100)]
_y = [3 * np.sin(5 * ele) + ele * 2 + 10 + random.random() for ele in _x]
# 设置初始参数
para_list = [random.random() for i in range(6)] # 索引从0到5分别表示 从常数位c x x^2 X^3 ..x^5的习俗
for i in range(1000):
for x, y in zip(_x, _y):
# 设置模型
h = para_list[1] * x + para_list[2] * (x ** 2) + para_list[3] * (x ** 3) + para_list[4] * (x ** 4) + para_list[5] * (x ** 5) + para_list[0]
# 均方误差损失函数
loss = (h - y) ** 2
# 求参数梯度 和给定学习率
grad_list = [2 * (h - y) * pow(x, i) for i in range(6)]
learn_ratio = 0.1
# 参数迭代更
for i in range(6):
para_list[i] -= learn_ratio * grad_list[i]
#图结果
plt.ion()
plt.plot(_x,_y,'.')
# 根据参数不断调整的模型图
plt.plot(_x,[para_list[1]*x + para_list[2] * (x**2) + para_list[3] * (x ** 3) + para_list[4] * (x ** 4) + para_list[5] * (x ** 5) + para_list[0] for x in _x])
plt.pause(5)
plt.cla()
效果:
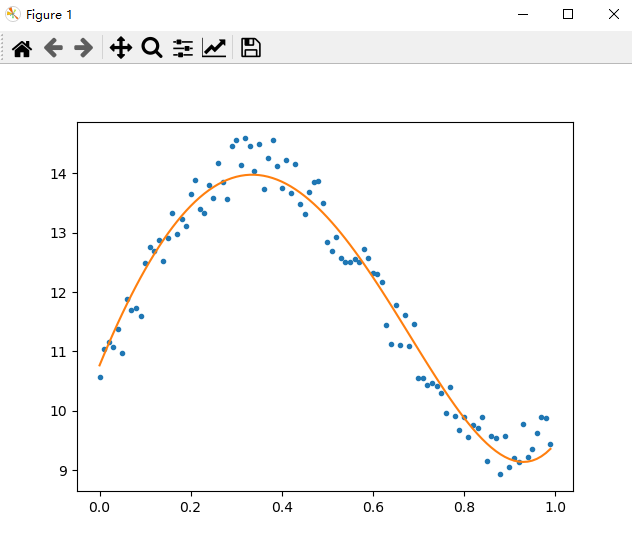
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Multimodal Contrastive Training for Visual Representation Learning
- 各语言冒泡排序总结
- python使用分治算法找出出现次数最多的数字
- Databend 部署与运维概要:本地部署 Meta 服务并利用 Kubernetes 管理 Query 服务
- 什么是序列化以及如何实现Java中的序列化?transient关键字的作用是什么?
- 基础_函数_数值函数
- Elasticsearch 字段更新机制
- toString()和JSON.stringify()有什么区别,分别在什么时候使用的?
- arm芯片安装lxml报错 libxslt.so.1: cannot open shared object file
- 基础算术运算符示例 - Python
