从信号处理角度彻底理解FFT

只想速览公式可以转到简明FFT公式

一、FFT起初用于解决的问题

分解复合信号
将复合信号视为若干正弦波与余弦波的叠加，如何得知某个正弦波/余弦波在该信号中的强度？

二、即答

用特定频率的正弦波/余弦波（设其为a）乘上复合信号即可
由三角函数系的正交性，对于复合信号中频率不同于a的波，与a相乘的结果在一个周期内积分为0；而对于频率与a相同的波，乘积在一个周期上的积分结果不为0，由此可以得到a在复合信号中的强度。（类似于码分多路复用，不知道不碍事，和FFT没关系）（不用担心相位问题，相位不为0的波可以分解成余弦波和正弦波）

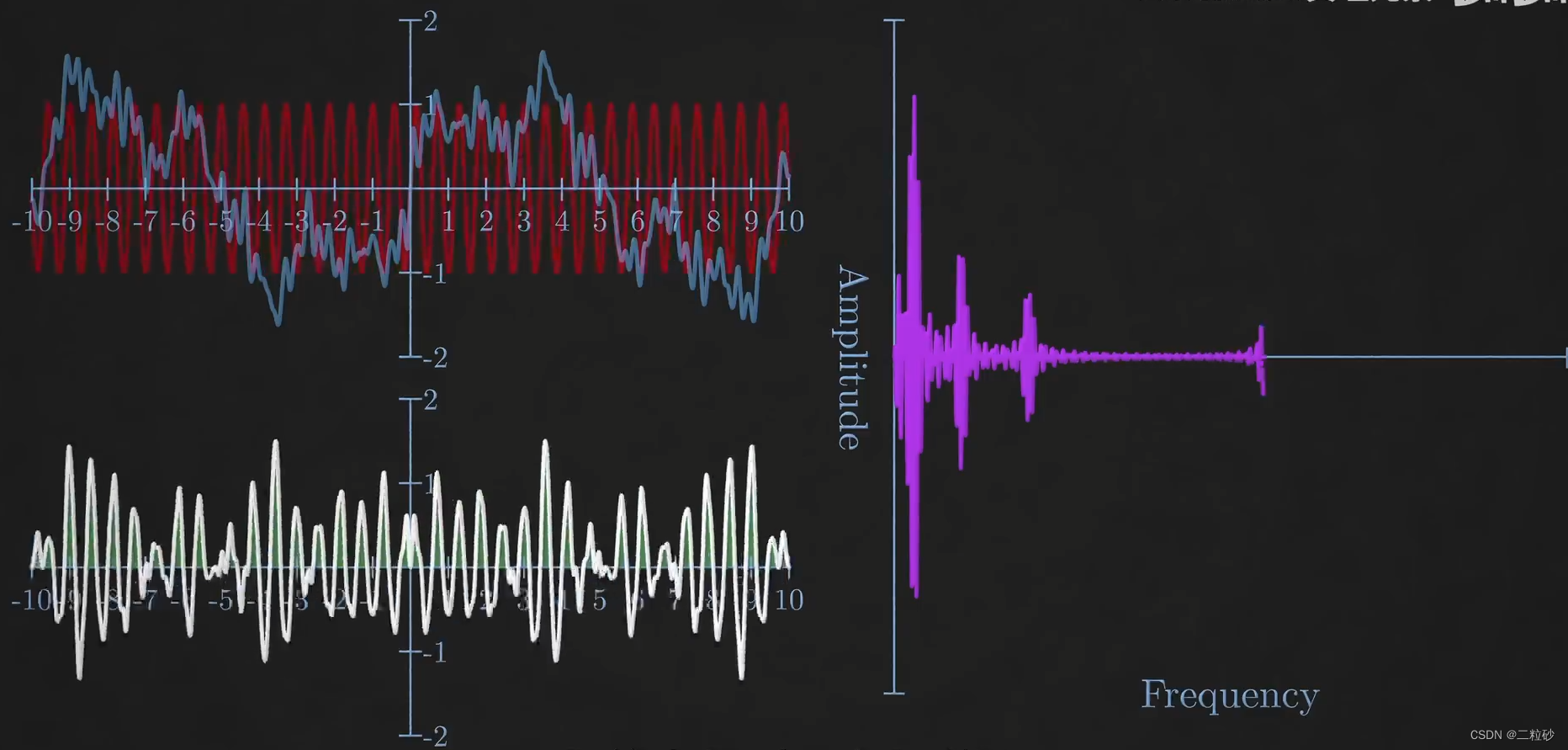
图中左上（记为图1），蓝的是原始信号，红的是给定频率的正弦波/余弦波a，是信号强度关于时间的函数（AKA时域）。图中左下（记为图2）是原始信号与a的乘积。图中右侧（记为图3）是不同频率的信号在原始信号中的强度，是信号强度关于频率的函数（AKA频域）。

如果某频率不存在于原始信号中，那么乘积的积分结果为0，对应于图3函数值接近于0的部分；如果某频率存在于原始信号中，那么乘积的积分结果不为0.对应于图3的峰值。

由图1中的蓝色曲线变成图3，这样的变换称为傅里叶变换（FT, Fourier Transform），也称由时域转换为频域；反之，为逆傅里叶变换（IFT, Inverse Fourier Transform），由频域转为时域。

那么把所有频率的正弦波和余弦波都和复合信号相乘再积分就好了，但这显然不现实

三、数学建模

1. 涉及到正弦波与余弦波

想到用欧拉公式，那么只用将信号乘上对应不同频率信号的指数就好

欧拉公式：$e^{ix}=cosx+isinx$

由于信号是关于时间的函数，并且和频率有关，因此写作$e^{i\omega t}$，其中$\omega$与频率f有关

问题变成：$F(f)={\int }_{?\infty }^{\infty }f(t)e^{?i\omega t}dt$，$f(t)$指原始信号。

2. 没法积分

现实中的信号往往用采样点表示，由此想到积分的极限形式，只不过这里n是有限的，即采样点的个数

问题变成：$F_f={\sum }_{n=0}^{N?1}{e}^{?i\omega n}{f}_n$，其中N是采样点个数，$f_n$是第n个采样点的信号强度

3. 没法乘所有频率

根据奈奎斯特采样定理，为了准确地重构一个连续时间信号，其采样频率必须至少是信号中最高频率成分的两倍。也就是说，可以有效地分辨出的信号的最大频率为采样频率的一半

因而要拿去乘原始信号的频率具体为 $f_k=(k/N)f_s，k=0,1,\mathrm{2...}N?1，f_s$是采样频率

举例来说，如果有8个采样点，那么就输出8个频率范围

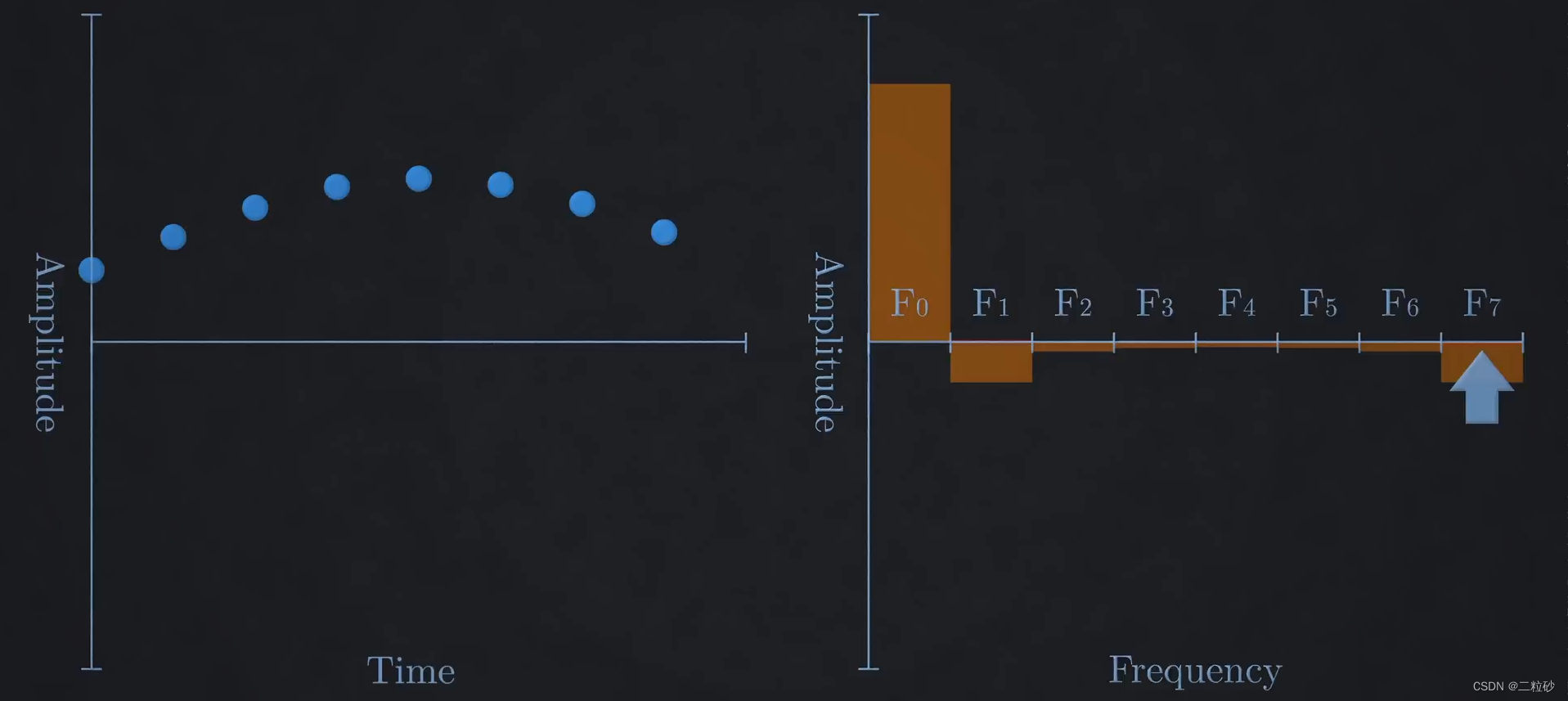
如果严格按照奈氏定理，k最大取到2/N，个人理解k取到N-1是为了考虑信号中的最高频率成分，而且根据FFT，高频部分与低频部分信号强度的计算共轭，顺手的事
如果有更科学的理解希望不吝赐教orz

因而要拿去乘原始信号的信号可以表示为$e^{?i\frac{2\pi }{N}kn},k=0,1,\mathrm{2...}N?1$

问题转化为$F_k={\sum }_{n=0}^{N?1}{e}^{?i\frac{2\pi }{N}kn}{f}_n，k=0,1,\mathrm{2...}N?1$

四、简化计算——FFT

上面的公式，对于每个特定频率，都要计算N次，一共有N个频率，时间复杂度为$O(N^2)$，Cooley提出简化。

以样本点个数为8，这8个数据要乘上8个频率的正弦波与8个频率的余弦波，这里以余弦波为例，按照三角函数的周期性，这些余弦波会以一定规律重叠，因此可以省去大量运算（如样本点$X_4$处，只用计算两次即可）

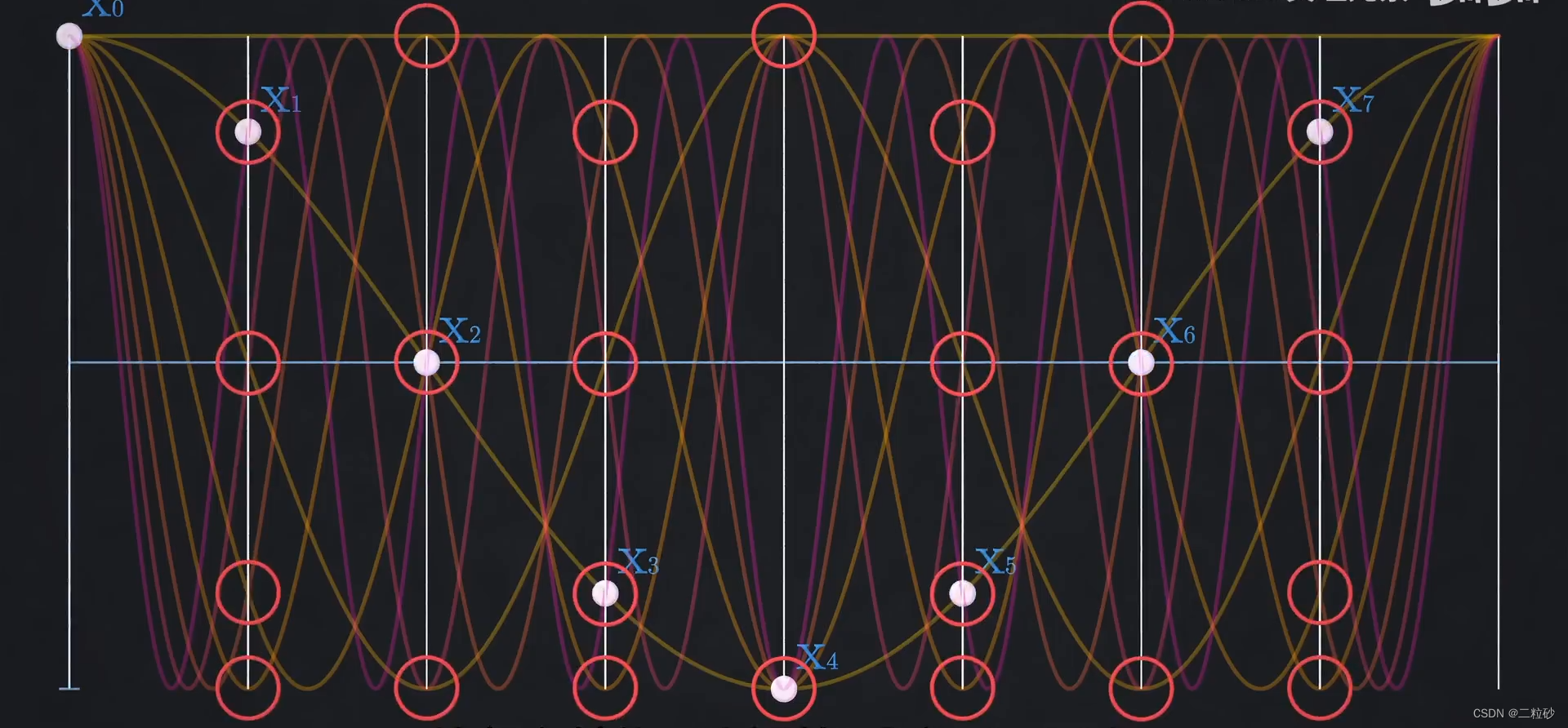
他将样本点按照顺序分成奇偶两组

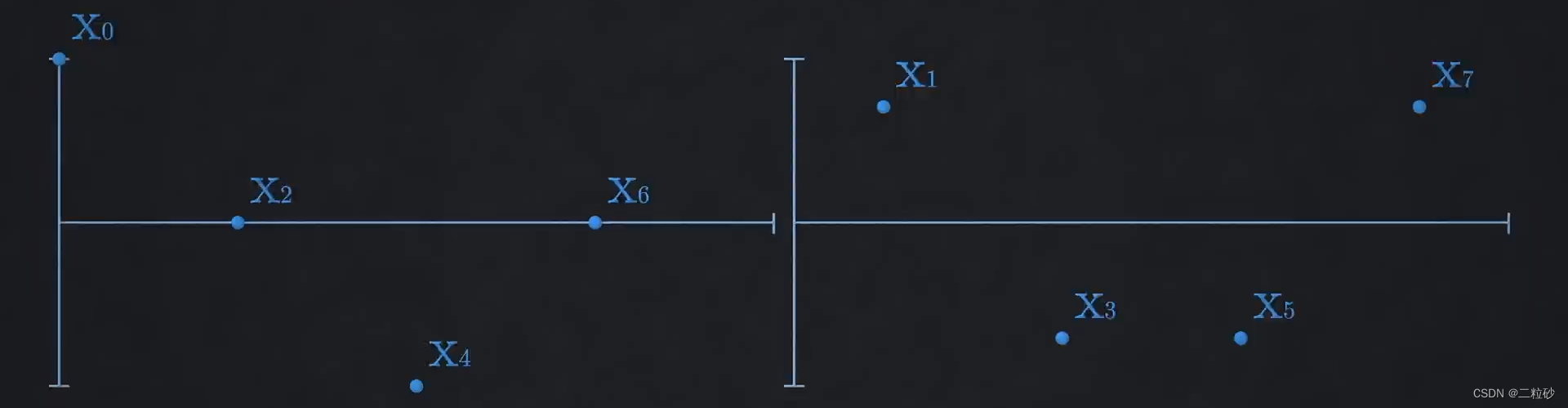
对于奇数点，以下是8个频率的余弦波，左侧是低频，右侧高频

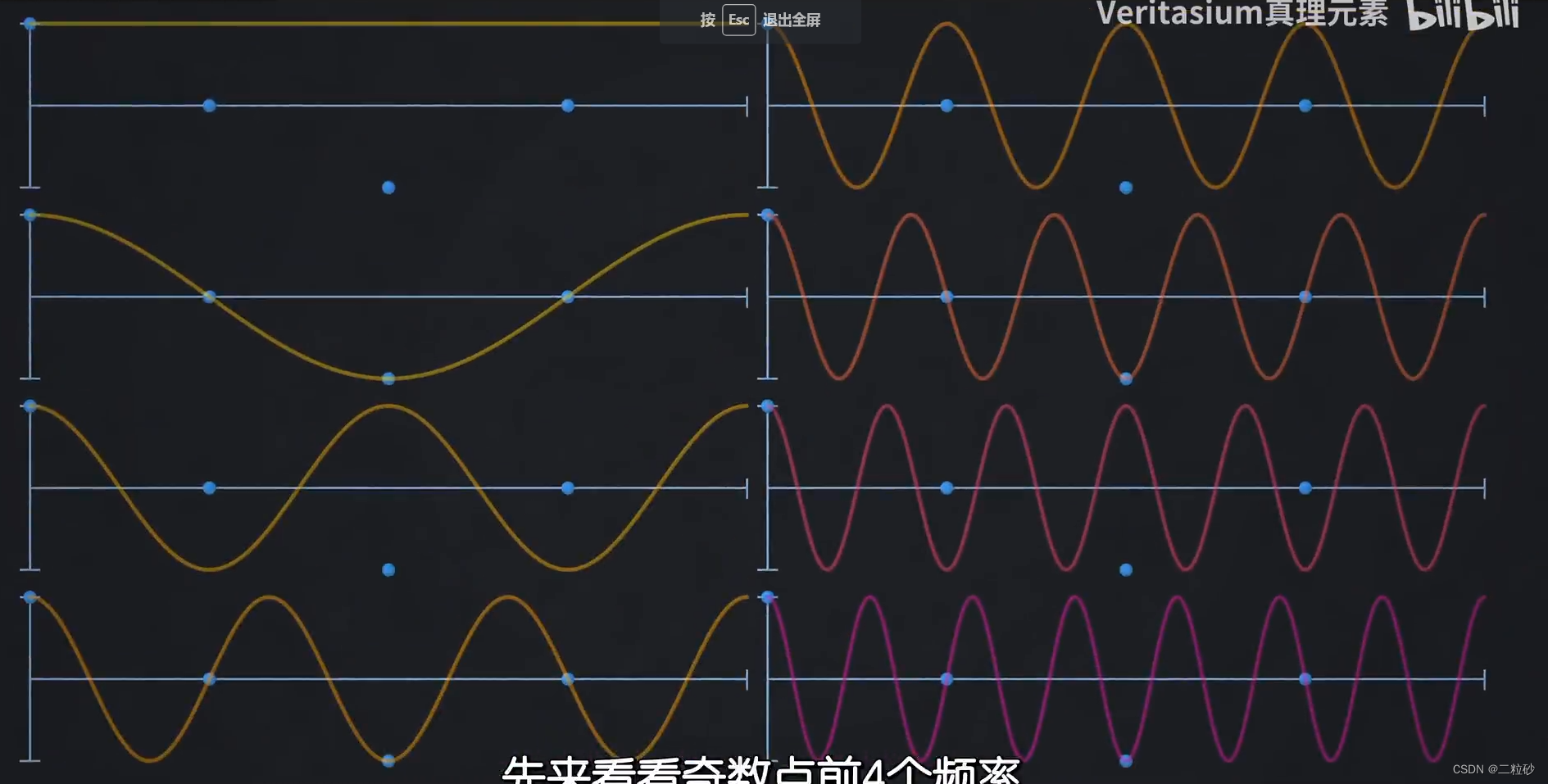
发现每个样本点位置都有两个频率的波取值相同（对于偶数点则是互为相反数）

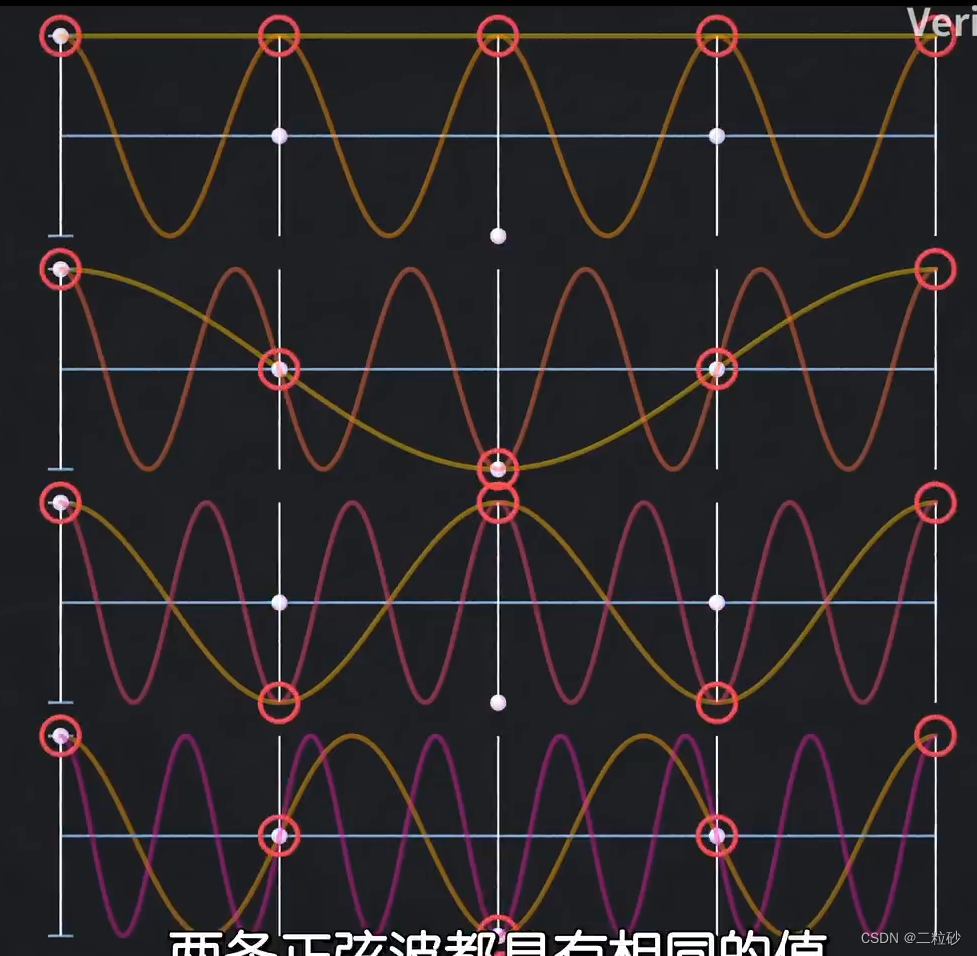
这意味着只用对低频部分做乘法并求和，高频部分可以直接复用低频结果，于是运算缩减到一半。而对于剩下的N/2个样本点，可以施以同样的方法，直到只剩一个样本点。于是时间复杂度变为$O(Nlo{g}_{2}N)$

这也是FFT最为广泛应用的Cooley-Turkey算法，具体公式可转到简明FFT公式
$$————————————————————————————————$$

参考：这个算法彻底改变了世界_哔哩哔哩