【详解】稀疏矩阵的十字链表????

目录

引言：

稀疏矩阵的十字链表表示

第一步：创结点存数据

第二步：将头结点同数据结点串起来

第三步：创建一个总头结点构成循环链表

总代码如下：

运行结果如下：

结语：

---

引言：

接上一小结稀疏矩阵的三元组表示（循序表表示），一般有循序表示就有链表表示，今天我们要介绍的就是稀疏矩阵的链表表示???

稀疏矩阵的十字链表表示

十字链表是稀疏矩阵的一种链式存储结构（我前一章写的三元组循序表是稀疏矩阵的一种循序存储结构），如果对三元组不了解的同学可以去我前面一章先看（超详细?）

接着让我们进入十字链表的创建步骤

为了方便大家理解我先给出图片大家可以先看看，行和列都到h【5】

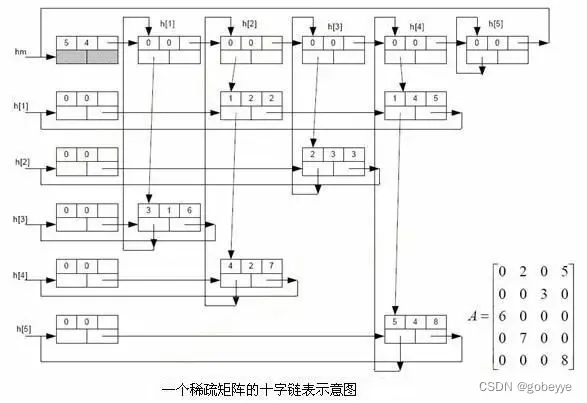
第一步：创结点存数据

既然是链表那么就一定有结点，对于稀疏矩阵中的每个非零元素创建一个结点存放它，存放的数据包括（1）元素行数（2）元素列数（3）元素值

代码如下 （因为增加通用性，故用ElemType方便修改）

union里面有value 和 link两个数据，其中value是存放数据结点的元素值，link是头结点的下一个结点，这里就体现了头结点的重要性，头结点-->link就是下一个结点，头结点-->right就是数据节点了，这样就可以把头结点和数据结点区分开来。

typedef int ElemType;
typedef struct mtxn 
{ 
	int row;					//行号
	int col;					//列号
   	struct mtxn *right,*down;	//向右和向下的指针
	union 
	{
		ElemType value;
		struct mtxn *link;
	} tag;
} MatNode;			//十字链表类型

第二步：将头结点同数据结点串起来

将同一行所有结点串成一个带头结点的循环单链表，将同一列所有结点串成一个带头结点的循环单链表，那么这里我们是不是可以合并呢，将行和列头结点放在一个数据结构里，这样是不是能跟方便一些呢，故我们只需创建MAX（行，列）个结点数，里面有行结点和列结点，这里是用right和down来实现的，头结点始终就那MAX（行，列）个，这里要好好理解。

void CreatMat(MatNode *&mh,ElemType a[][N])	//创建a的十字链表
{
	int i,j;
	MatNode *h[Max],*p,*q,*r;
	mh=(MatNode *)malloc(sizeof(MatNode));//创建十字链表的头结点
	mh->row=M;mh->col=N;
	r=mh;					//r指向尾结点
	for (i=0;i<Max;i++)		//采用尾插法创建头结点h1,h2,…循环链表
	{
		h[i]=(MatNode *)malloc(sizeof(MatNode));
		h[i]->down=h[i]->right=h[i];		//将down和right方向置为循环的
		r->tag.link=h[i];					//将h[i]加到链表中
		r=h[i];
	}
	r->tag.link=mh;							//置为循环链表
	for (i=0;i<M;i++)						//处理每一行
	{
		for (j=0;j<N;j++)					//处理每一列
		{
			if (a[i][j]!=0)					//处理非零元素
			{
				p=(MatNode *)malloc(sizeof(MatNode));	//创建一个新结点
				p->row=i;p->col=j;p->tag.value=a[i][j];
				q=h[i];      					//查找在行表中的插入位置
                while (q->right!=h[i] && q->right->col<j) 
                  	q=q->right;
				p->right=q->right;q->right=p;	//完成行表的插入
				q=h[j];      					//查找在列表中的插入位置
				while (q->down!=h[j] && q->down->row<i) 
					q=q->down;
				p->down=q->down;q->down=p;  	//完成列表的插入
			}
		}
	}
}

第三步：创建一个总头结点构成循环链表

创建一个总头结点方便进行插入删除的各种操作，并有利于查找数据，大家在刷力扣题时，有碰到链表一般都要自己创建一个头结点。

图画如下

以上便是稀疏矩阵的十字链表的创建方法。

创建完那么我们就要开始学习它的基本运算啦~~~~~🎉🎉🎉

---

创建上面已经给出故这里跳过

void DestroyMat(MatNode *&mh)?? ??? ?//销毁十字链表

一定要注意先后顺序，先释放数据结点再释放头结点循序不能乱，不然内存会泄露（不要内存泄漏🙅?），最后不要忘了要把总结点free掉哦。

void DestroyMat(MatNode *&mh)		//销毁十字链表
{
	MatNode *pre,*p,*mp;
	mp=mh->tag.link;				//mp指向h[i]
	while (mp!=mh)					//释放所有数据结点
	{
		pre=mp->right;				//pre指向h[i]的行首结点
		if (pre!=mp)				//h[i]不空
		{
			p=pre->right;			//p指向结点pre的后继结点
			while (p!=mp)
			{
				free(pre);
				pre=p; p=p->right;
			}
		}
		mp=mp->tag.link;			//mp指向下一个头结点
	}
	//释放所有的头结点
	pre=mh->tag.link;				//pre指向h[i]
	p=pre->tag.link;				//p指向h[i+1]
	while (p!=mh)
	{
		free(pre);
		pre=p; p=p->tag.link;
	}
	free(mh);
}

void DispMat(MatNode *mh)?? ??? ?//输出十字链表

这应该是大家最希望看到的吧，不然我们这么知道我们到底做了些上面呢

注意注意这里是按行开始打印，可以按列哦

用一个循环将所有数据全部输出即可

void DispMat(MatNode *mh)		//输出十字链表
{
	MatNode *p,*q;
	printf("行=%d  列=%d\n", mh->row,mh->col);
	p=mh->tag.link;
	while (p!=mh) 
	{	
		q=p->right;
		while (p!=q) 		//输出一行非零元素
		{
			printf("%d\t%d\t%d\n", q->row,q->col,q->tag.value);
			q=q->right;
		}
		p=p->tag.link;
	}
}

总代码如下：

先创建再打印后销毁，前面最开头一定不要忘了头文件，和#define各项数据哦👌

创建是先头结点后数据结点，销毁是先数据结点后头结点，打印是用头结点去找数据结点，并按照行或列进行打印。

#define  _CRT_SECURE_NO_WARNINGS 1
//稀疏矩阵的十字链表表示
#include <stdio.h>
#include <stdlib.h>
#define M 3
#define N 4
#define Max 4
typedef int ElemType;
typedef struct mtxn
{
	int row;
	int col;
	struct mtxn* right, * down;
	union {
		ElemType value;
		struct mtxn* link;
	}tag;
}MatNode;
void CreateMat(MatNode* mh, ElemType a[][N])
{
	MatNode* h[Max];
	mh->row = M; mh->col = N;
	MatNode* r = mh;
	for (int i = 0; i < Max; i++)
	{
		h[i] = (MatNode*)malloc(sizeof(MatNode));
		h[i]->down = h[i]->right = h[i];
		r->tag.link = h[i];
		r = h[i];
	}
	r->tag.link = mh;
	for(int i =0;i<M;i++)
		for (int j = 0; j < N; j++)
		{
			if (a[i][j] != 0)
			{
				MatNode* p = (MatNode*)malloc(sizeof(MatNode));
				p->row = i; p->col = j; p->tag.value = a[i][j];
				MatNode* q = h[i];
				while(q->right != h[i] && q->right->col < j) q = q->right;
				p->right = q->right; q->right = p;
				q = h[j];
				while (q->down != h[j] && q->down->row < i) q = q->down;
				p->down = q->down; q->down = p;
			}
		}
}
void DispMat(MatNode* mh)		//输出十字链表
{
	MatNode* p, * q;
	printf("行=%d  列=%d\n", mh->row, mh->col);
	p = mh->tag.link;
	while (p != mh)
	{
		q = p->right;
		while (p != q) 		//输出一行非零元素
		{
			printf("%d\t%d\t%d\n", q->row, q->col, q->tag.value);
			q = q->right;
		}
		p = p->tag.link;
	}
}
void DestroyMat(MatNode* mh)
{
	MatNode* pre, * p, * mp;
	mp = mh->tag.link;
	while (mp != mh)
	{
		pre = mp->right;
		while (pre != mp)
		{
			p = pre->right;
			free(pre);
			pre = p;
		}
		mp = mp->tag.link;
	}
	pre = mh->tag.link;
	while (pre != mh)
	{
		p = pre->tag.link;
		free(pre);
		pre = p;
	}
	free(mh);
}
int main()
{
	ElemType a[M][N] = { {1,0,0,2},{0,0,3,0},{0,0,0,4} };
	MatNode* t = (MatNode*)malloc(sizeof(MatNode));
	CreateMat(t,a);
	DispMat(t);
	DestroyMat(t);
	return 0;
}

运行结果如下：

😃😃😃😃😃

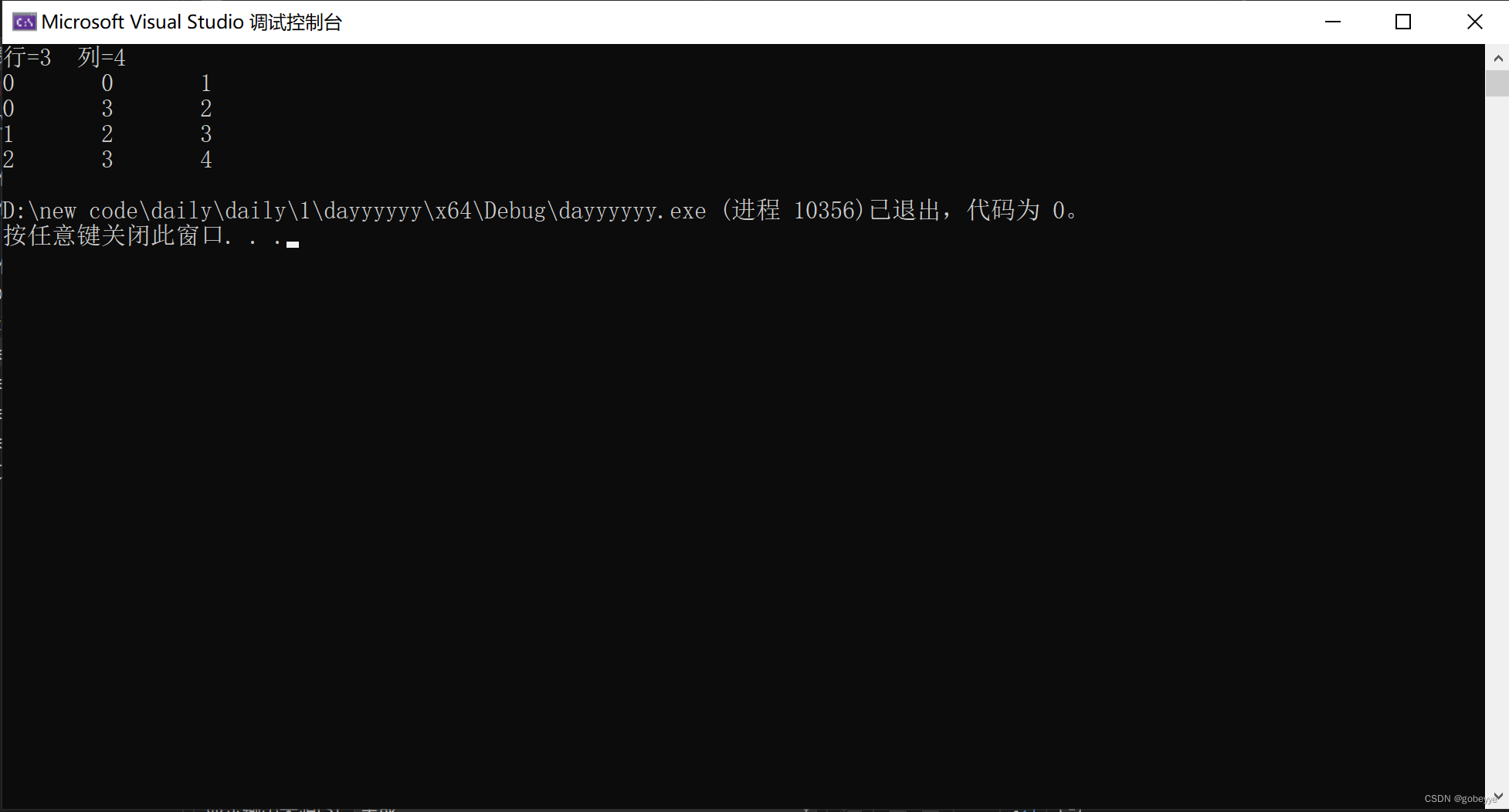
总结：我们可以看到稀疏矩阵的十字链表是三元组的改进，运用这两种方法可以很好的解决稀疏矩阵的存储问题，从而节省空间，至于这两种要选择哪一个要看具体情况和自身对那个比较熟练。

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固自己的知识点，和一个学习的总结，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进，如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注，这可以激励我写出更加优秀的文章。