代码随想录算法训练营day2|977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II
第一章??数组part02?
977.有序数组的平方?,209.长度最小的子数组?,59.螺旋矩阵II?,总结?
?977.有序数组的平方?
题目建议:?本题关键在于理解双指针思想?
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
文章讲解:代码随想录
视频讲解:?双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili
?209.长度最小的子数组
题目建议:?本题关键在于理解滑动窗口,这个滑动窗口看文字讲解?还挺难理解的,建议大家先看视频讲解。??拓展题目可以先不做。?
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
文章讲解:代码随想录
视频讲解:拿下滑动窗口! | LeetCode 209 长度最小的子数组_哔哩哔哩_bilibili
?59.螺旋矩阵II
题目建议:??本题关键还是在转圈的逻辑,在二分搜索中提到的区间定义,在这里又用上了。?
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
文章讲解:代码随想录
视频讲解:一入循环深似海 | LeetCode:59.螺旋矩阵II_哔哩哔哩_bilibili
?总结?
文章链接:代码随想录

? ? ? ? 最直观的方法就是遍历数组并平方,然后对新数组排序,排序如果使用冒泡的话,输入规模最大1e4,在O(n^2)下就是1e8,估计会超时的,试了一下确实超时了。O(nlogn)的排序算法下1e6可以试一下。
1.C++标准库中的<vector>中包含了一个内置的sort函数,用于对vector容器中的元素进行排序。sort函数使用的是快速排序(Quicksort)算法,具有时间复杂度为O(nlogn)。
2.C++标准库中的sort函数使用的是一种混合了快速排序(Quicksort)和插入排序(Insertion Sort)的排序算法,具体是使用的是Introsort算法。
Introsort算法在排序的过程中,首先使用快速排序来快速地进行划分,当快速排序的递归深度超过一定限制时,为了避免快速排序的最坏情况时间复杂度O(n^2)的发生,转而使用插入排序,这样可以保证时间复杂度不会超过O(nlogn)。
c++代码示例如下O(n+nlogn)
vector<int>sortedSquares(vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
nums[i] *= nums[i];
}
sort(nums.begin(), nums.end(), less<int>());
return nums;
}? ? ? ? 双指针法
可以发现数组负数部分平方后从大到小,正数部分平方后从小到大。如图
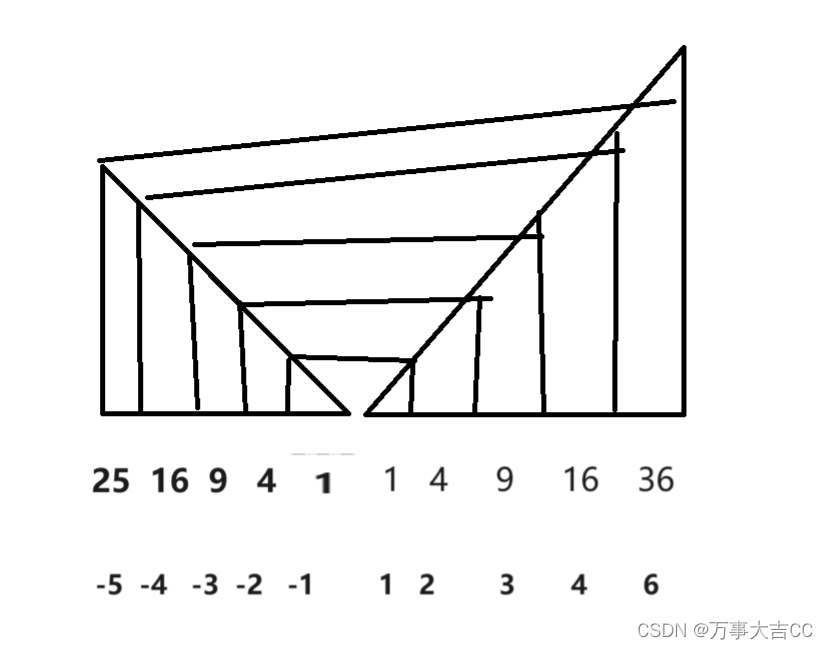
数组最大的数满足max{左端,右端},使用双指针,i指向左起始位置,j指向右起始位置。定义一个和数组同样大小的新数组ret,k指向ret数组右起始位置。
每次比较左右起始位置值大小,并把较大值添加至ret数组尾。更新较大值指针、ret数组右起始位置k。
动画如图

c++代码示例如下O(n)
vector<int>sortedSquares(vector<int>& nums) {
int k = nums.size() - 1;
vector<int>ret(nums.size(), 0);
for (int i = 0, j = nums.size() - 1; i <= j;) {
if (nums[i] * nums[i] >= nums[j] * nums[j]) {
ret[k--] = nums[i] * nums[i];
i++;
}
else {
ret[k--] = nums[j] * nums[j];
j--;
}
}
return ret;
}
? ? ? ? 直观的暴力方法就是遍历数组,定义len为一个大数,每次以i为起始求满足情况的最短连续子序列,记录长度并与len做判断,若小于则更新len。最后输出结果,若len没有更新则表示没有满足情况的子序列,返回0。
c++代码示例如下O(n^2)
int minSubArrayLen(int target, vector<int>& nums) {
int lmin = INT32_MAX;
int sum = 0;
for (int i = 0; i < nums.size(); i++) {
sum = 0;
for (int j = i; j < nums.size(); j++) {
sum += nums[j];
if (sum >= target) {
int len = j - i + 1;
lmin = len < lmin ? len : lmin;
}
}
}
return lmin == INT32_MAX ? 0 : lmin;
}超时了
? ? ? ? 在暴力解法中,一个for循环指向子序列头,嵌套一个for循环指向子序列尾,用两个循环完成了不断搜索区间的过程。在实际运行中,假设存在多个连续子序列,第一次找的子序列1后,在第二次找子序列2的时候,更新头指针也就是外循环,然后回溯尾指针也就是内循环。实际上下次寻找子序列的时候,上一次尾指针可以复用,子序列1由头尾指针确定的区间和大于等于target,可以证明若仅更新头指针,复用尾指针所得区间和是符合题意的。这个更新是精髓。
? ? ? ? 也就是双指针法了,由于这种解法更像是一个窗口的滑动,故命名为滑动窗口。虽然我觉得跟毛毛虫一样
下面以题目中的示例来演示滑动窗口的起始位置是怎么移动的。s=7,数组{2,3,1,2,4,3}来看一下查找的过程。
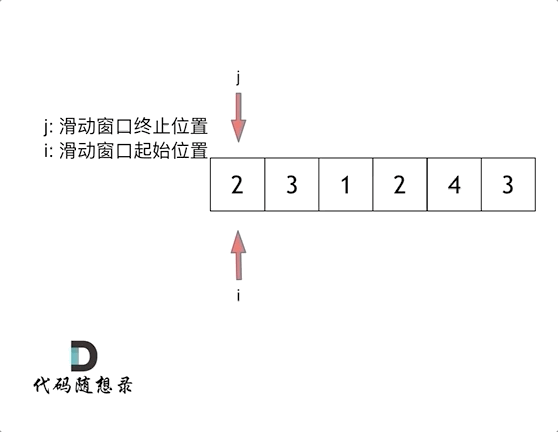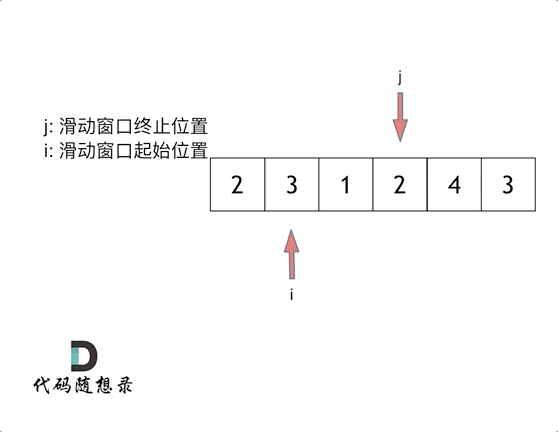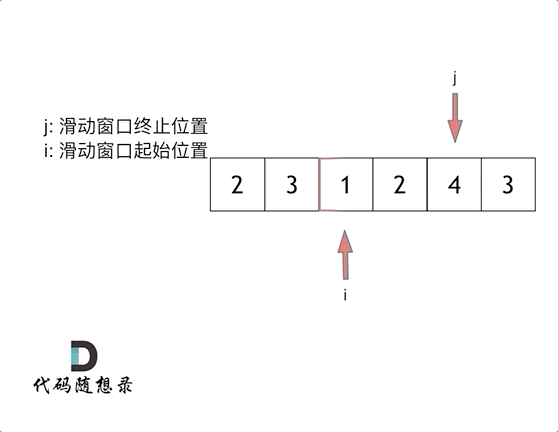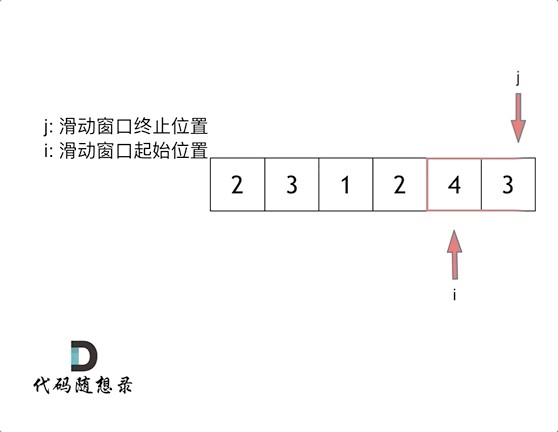
c++代码示例如下O(n)
int minSubArrayLen(int target, vector<int>& nums) {
int lmin = INT32_MAX;
int sum = 0, i = 0, len = 0;
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
while (sum >= target) {
len = j - i + 1;
lmin = len < lmin ? len : lmin;
sum -= nums[i++];
}
}
return lmin == INT32_MAX ? 0 : lmin;
}
? ? ? ? 简单的模拟题。解法可以分为二类,如图
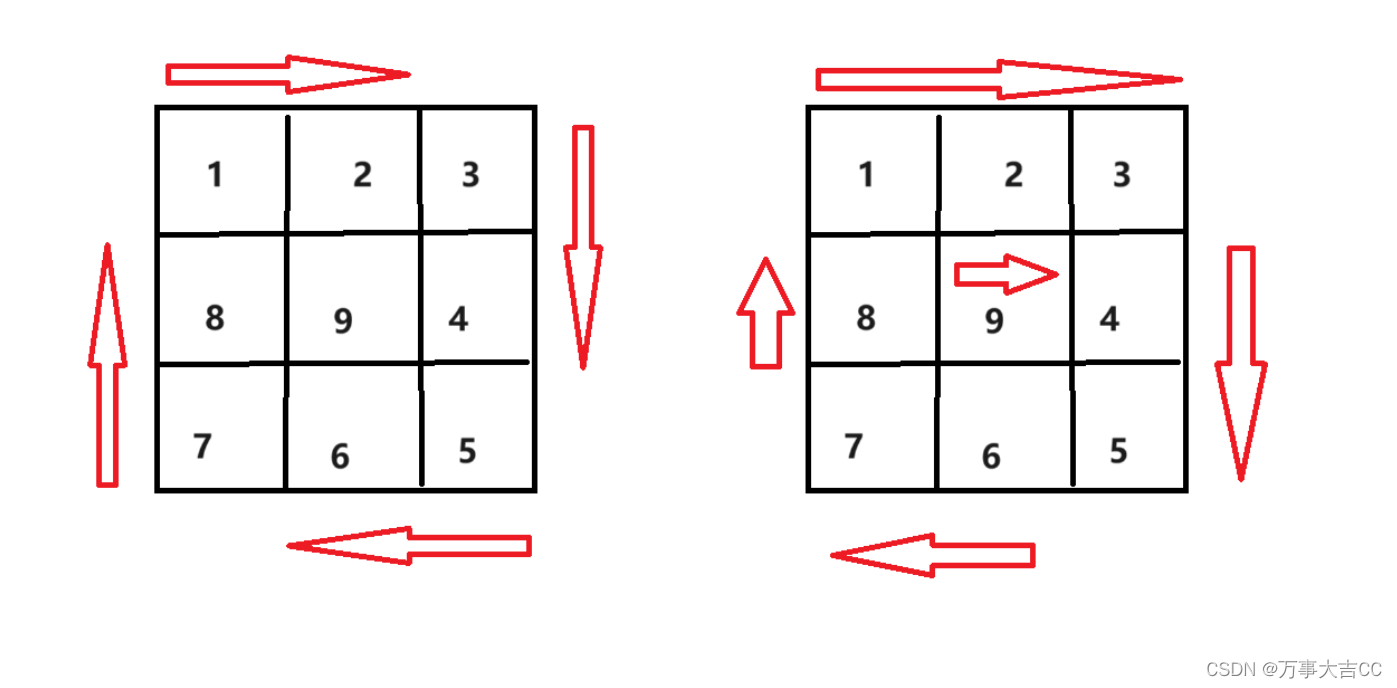
左边写法在边长为奇数时需要单独补中心,右边写法则通用
由上,右,下,左的模拟行为里的区间定义决定。
c++代码示例如下
vector<vector<int>> generateMatrix(int n){
vector<vector<int>> res(n, vector<int>(n, 0));
int startx = 0, starty = 0;
int loop = n / 2;
int cnt = 1;
int offset = 1;
int i, j;
while (loop--) {
i = startx;
j = starty;
for (j = starty; j < n - offset; j++) res[i][j] = cnt++;
for (i = startx; i < n - offset; i++) res[i][j] = cnt++;
for (; j > starty; j--) res[i][j] = cnt++;
for (; i > startx; i --) res[i][j] = cnt++;
startx++; starty++;
offset += 1;
}
if (n % 2) res[n / 2][n / 2] = cnt;
return res;
}——未完待续
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!