格密码基础：详解LWE问题

发布时间：2024年01月19日

一. 介绍

二. LWE分布

三. LWE问题的两个版本

一. 介绍

Learning With Errors 简称 LWE，通常翻译为容错学习问题。

在2005年，Regev首次提出了平均情况下的LWE问题。类似SIS问题，LWE也可以用来实现加密。这两类问题实际上互为对偶（dual）关系。接下来我们将介绍LWE的困难性以及基于LWE的密码系统。进阶的内容则包含LWE最坏情况的困难性，以及search和decision版本之间的归约。

SIS问题可参看：

格密码基础：SIS问题的定义与理解-CSDN博客

二. LWE分布

LWE问题有三个重要的参数：整数n，模q和整数上的误差分布X。此处的n和q的理解与SIS类似，分布X可以看成离散高斯分布，其宽度（width）为：

$\alpha q\quad \alpha<1$

此处的宽度类似高斯分布的标准差，可以被称之为相对误差率（relative error rate）。

备注：对于连续的高斯分布（continuous Gaussian distribution），借鉴随机离散化算法便可以形成离散的高斯分布（直观上，我们可以看成对连续高斯分布进行就近取整）。

有一个n维的秘密列向量s，如下：

$s\in Z_q^n$

均匀且随机的选择一个公开的n维列向量a：

$a\in Z_q^n$

接着从分布X中随机选择e：

$e\leftarrow X$

接着计算如下：

$(a,b=\langle s,a\rangle+e\quad mod\ q)$

随着a在不断变化，该形式可形成一个分布，我们称之为LWE分布。再根据a和b的形式，可得该分布的维度如下：

$Z_q^n\times Z_q$

三. LWE问题的两个版本

LWE问题最常用两个版本。给出LWE的样本，让你去求秘密向量s，则称之为search问题。

抽取LWE样本，从均匀且随机的分布中抽取样本，让你进行区分这两种情况，称之为decision问题。

细心的小伙伴会发现，以上抽取样本，通常有多少个呢？

可设定为样本个数有m个，当然为了保证秘密s唯一可解，通常需要要求m>n。这也是LWE问题与SIS问题的区别之一。

3.1 search LWE问题

我们通常将LWE分布记作：

$A_{s,X}$

对于固定的秘密向量s：

$s\in Z_q^n$

从LWE分布中随机抽取m个独立的样本，如下：

$(a_i,b_i)\in Z_q^n\times Z_q$

根据这些样本，求取s的过程，则称之为LWE-search问题，完整表达如下：

$Search-LWE_{n,q,X,m}$

完整的英文形式化表达如下：

3.2 decision LWE问题

给定m个独立的样本，如下：

$(a_i,b_i)\in Z_q^n\times Z_q$

这些样本来源的分布有两种情况：

（1）均匀随机的 $s\in Z_q^n$ ，接着固定s，形成分布 $A_{s,X}$

（2）真均匀且随机的分布

如果能以不可忽略的优势区分这两种情况，才可以称之为解决了decision LWE问题。

四. LWE的性质

4.1 误差e的重要性

如果没有来源于分布X的误差项，那么以上LWE问题就都可以被解决。比如借助高斯消元法（Gaussian elimination）可以从LWE样本中恢复出s。

在decision-LWE问题中，对于真均匀分布的情况，可以大概率确定s不存在，也就可以区分开来了。

4.2 矩阵形式

在网络安全等领域，通常会把以上样本结合成矩阵A:

$A\in Z_q^{n\times m}$

矩阵A的每一列都代表一个向量 $a_i\in Z_q^n$

同理，b也可以形成向量：

$b\in Z_q^n\quad b_i\in Z_q$

结合以上形式，我们可以将LWE样本写成：

其中误差e：

$e\leftarrow X^m$

如果是真的成均匀分布中选取，也就是在decision LWE问题中,b就是真随机的，且与矩阵A无关。

4.3 LWE与BDD问题

bounded-distance decoding 简称?BDD，中文通常翻译为：有限距离解码问题

我们知道，对于任意LWE样本，向量b与LWE格是很接近的，中间差一个误差e。LWE就是我们通常所说的m维q-ary格，如下：

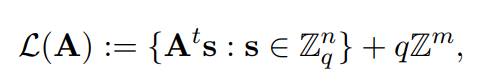
所以可以把LWE问题看成寻找格点的过程，也就可以把search-LWE问题看成平均情况的BDD问题。

如果向量b来源于均匀分布，那么其大概率跟格L(A)中的所有格点都很远。

根据LWE与SIS之间的关系，其实我们可以得到两者之间互为q倍对偶关系：

4.4 LWE与隐藏超平面问题

观察LWE的样本：

$(a_i,b_i)\in Z_q^{n+1}$

可对样本的横坐标与纵坐标做如下运算：

那么我们可以发现LWE跟垂直于（-s,1）的子空间很接近，当然所有的运算都在模q下，所以我们发现这个跟Ajtai-Dwork发现的隐藏超平面问题非常类似。

五. 推荐文献

（1）解释LWE与隐藏超平面之间的关系

O. Regev. The learning with errors problem (invited survey). In IEEE Conference on Computational Complexity, pages 191–204. 2010.

（2）完整介绍LWE问题

O. Regev. On lattices, learning with errors, random linear codes, and cryptography. J. ACM,
56(6):1–40, 2009. Preliminary version in STOC 2005.

（3）Regev对格密码介绍的课件

O. Regev. Lecture notes on lattices in computer science, 2004. Available at http://www.cs.
tau.ac.il/?odedr/teaching/lattices_fall_2004/index.html, last accessed 28 Feb 2008.

文章来源:https://blog.csdn.net/forest_LL/article/details/135695351
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！