Codeforces1203A Circle of Students题解+标程

题目传送门

题意：

? ? ? ? n个学生按一定顺序排成圆圈，在某些条件下（如题）可以跳圆圈舞，询问该组学生能否按顺/逆时针跳圆圈舞。

题解：

? ? ? ? 根据题意和样例，不难发现，n个学生要满足跳舞的条件，他们围成一圈时的编号必须从某一位开始一直递增/递减。

? ? ? ? 比如：

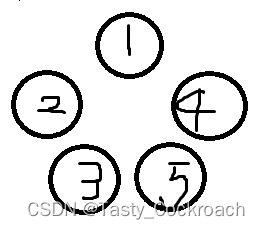
3? ? 2? ? 1? ? 5? ? 4

从①开始沿着逆时针，学生编号不断递增?，所以可以

而

1? ? 2? ? 3? ? 5? ? 4? ?（此处图画反了，原题是学生顺时针排列）

这个样例中，从①开始沿逆时针，学生编号在3->5和4->1的位置断开了，不是递增或者递减

?????????为了保证这个环从某一元素出发是递增或递减的，我们可以看相邻两数之间差的绝对值。要做到递增/递减，则相邻两个数之间应差1，又因为给出的是一个环的排列，所以头尾之间的差也需要考虑。

? ? ? ? 当只有一处相邻点的差不为1时（即该递增/递减序列头与尾的差），这个环才能从某一处拆成一个递增/递减序列。

理论成立，代码开始：

#include<bits/stdc++.h>
using namespace std;
int Q,n,p[205];
int main()
{
	cin>>Q;
	while(Q--)
	{
		cin>>n;
		for(int i=1;i<=n;i++)
		{
			cin>>p[i];
		}

到这里都是很平常的输入

		int num=0;
		for(int i=2;i<=n;i++)
		{
			if(abs(p[i]-p[i-1])!=1)
			{
				num++;
			}
		}

此处为判断相邻两个点的差不为1的交接点有多少，以num储存

        if(abs(p[1]-p[n])!=1)
		{
			num++;
		}

在循环里没有判断到的头尾之差放在循环外判断

		if(num>1)
		{
			cout<<"NO"<<endl;
		}
		else
		{
			cout<<"YES"<<endl;
		}
	}
	return 0;
}

最后判断不为1的数量是否大于一，如果是那说明这个环不成立，无法跳舞。直接美美输出，return 0完美收尾~