数据存储细节
整型家族:char? short? int? long
计算机的整型都是用补码表示的

补码存在的意义(CPU只能进行加法,原码不能满足需要):


数据存储大小端的概念

大端/小端:大端字节序存储模式/小端字节序存储模式


判断大小端程序设计


优化版本

还有一种巧妙的方法利用共用体的结构。详见共用体章节
整型提升
C语?中整型算术运算总是?少以缺省整型类型的精度来进行的。 为了获得这个精度,表达式中的字符和短整型操作数在使?之前被转换为普通整型,这种转换称为整型提升。
整型提升的意义
表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。 因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
通?CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int?度的整型值,都必须先转换为 int或unsigned int(取决于原数据的类型有无符号),然后才能送?CPU去执行运算。
整型提升的示例
//实例1
char a,b,c;
...
a = b + c;b和c的值被提升为普通整型,然后再执行加法运算。 加法运算完成之后,结果将被截断,然后再存储于a中。
整体提升的方法
1. 有符号整数提升是按照变量的数据类型的符号位来提升的
2. ?符号整数提升,高位补0
举例说明
负数的整形提升
char c1 = -1; 变量c1的?进制位(补码)中只有8个比特位: 1111111 因为 char 为有符号的 char 所以整形提升的时候,?位补充符号位,即为1 提升之后的结果是: 11111111111111111111111111111111
正数的整形提升
char c2 = 1; 变量c2的?进制位(补码)中只有8个比特位: 00000001 因为 char 为有符号的 char 所以整形提升的时候,?位补充符号位,即为0 提升之后的结果是: 00000000000000000000000000000001
习题1

-1的补码是11111111 11111111 11111111 11111111,因为是char类型截断后的补码是11111111(保留原来补码的低8位)
整型提升按照原符号位进行提升
char默认有符号,则最高位就是他的符号位:1111 1111--->11111111 11111111 11111111 11111111(补码,提升之后的结果)---->算源码还是-1
signed char??????? 则最高位就是他的符号位:1111 1111--->11111111 11111111 11111111 11111111(补码,提升之后的结果)---->算源码还是-1
unsigned char??? 最高位不是他的符号位,无符号数,高位提升时补0:1111 1111--->00000000 00000000 00000000 11111111---->最高位是0,表示正数255,正数的原反补码相同
习题2

1000 0000(符号位是1,整型提升补1)--->11111111 11111111 11111111 10000000
char整型提升(补码)的步骤:
1.看原char是无符号还是有符号
2.有符号整数提升是按照变量的数据类型的符号位来提升的。无符号整数提升,高位补0。
3.char类型运算后不放在char类型就不需要截断,运算后的结果直接用%d/%u打印。
打印相关注意事项:
打印有无符号整型(%d/%u)-->算出整型提升之后的补码--->看打印类型--->1.%d:有符号整型,由补码算出源码? 2.%u无符号整型,补码==反码==源码
结论
一个数据像-1、1默认都是以32位(int型)存储的,如果放在char型或short型就要发生截断
char类型运算时要进行整型提升,提升后如果要放到char类型里还要截断其他位(除了低八位),char要用%d/%u打印也要进行整型提升。
数据的递增/递减方向的数值轮回




习题3

习题4

习题5

习题6

习题7

i是无符号数,永远为正
10 9 8 7 6 5 4 3 2 1 0 2^32-1(-1的补码是32个1)...........死循环
习题8
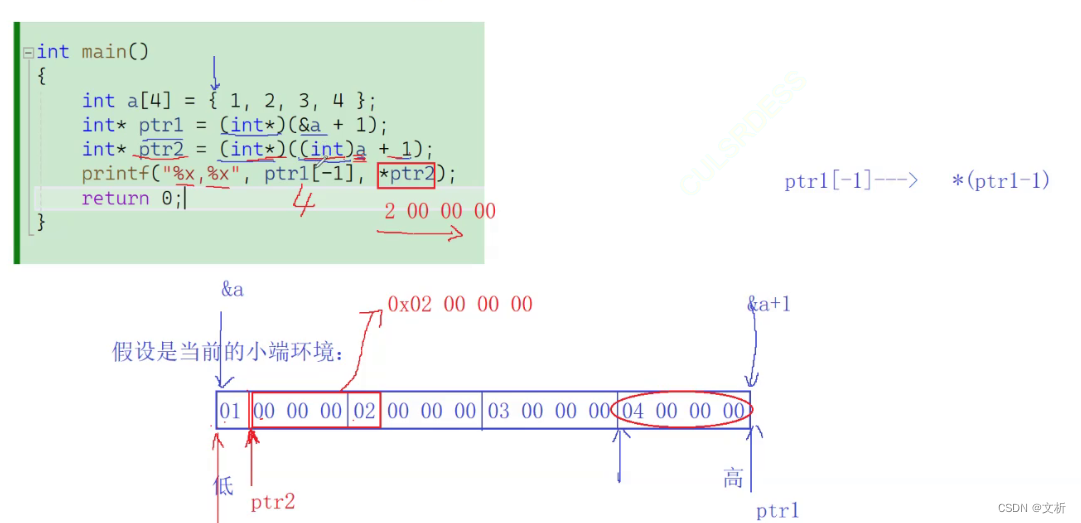
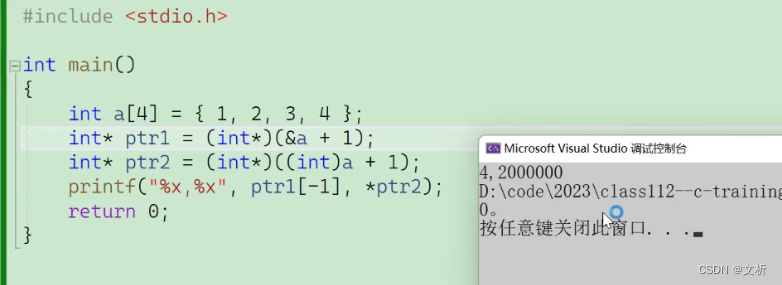
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Numpy数值计算
- k8s的集群调度
- STM32中TIM定时器定时功能详解(适用基本,通用,高级定时器)
- tomcat剖析:开篇
- python中collections.abc.Mapping 和collections.Mapping的区别
- 简洁高效的 NLP 入门指南: 200 行实现 Bert 文本分类 TensorFlow 代码纯享版
- 从信号处理角度彻底理解FFT
- electron 主进程对预加载脚本和渲染进程通信
- Linux设置Nginx开机自启以及指定脚本
- 四、HTML 属性