二叉搜索树介绍以及实现

????????二叉树无论是在实际运用还是面试题中，都是一种十分热门的数据结构，而二叉搜索树则是进阶版的二叉树，在map和set中也有应用。

什么是二叉搜索树

二叉搜索树又叫二叉排序树，它可以是一颗空树，又或者是有以下三个特点的树。

• 若它的左子树不为空，则左子树的所有节点的值都小于根节点的值。
• 若它的右子树不为空，则右子树的所有节点的值都大于根节点的值。
• 它的左右子树也都是二叉搜索树。

因为二叉搜索树具有以上三个特性，因此二叉搜索树的最优搜索次数为 O(log^2) ，最差搜索次数为 O(N)。

此外，中序遍历一个二叉搜索树所得到的结果应该是一个有序的数组。

二叉搜索树的实现

二叉搜索树的查找

• 从根节点开始查找，若查找的 val 大于根节点的值，则向右子树查找，否则向左子树查找
• 最多查找高度次，走到空还没有找到，就返回nullptr,否则就返回这个节点。

pNode find(const T& val)
{
	pNode cur = Root;
	if (cur->_data == val)
	{
		return cur;
	}
	while (cur != nullptr)
	{
		if (val > cur->_data)
		{
			cur = cur->_right;
		}
		else if (val < cur->_data)
		{
			cur = cur->_left;
		}
		else
		{
			return cur;
		}
	}
	return nullptr;
}

二叉搜索树的插入

?二叉树的插入需要找到正确的位置。

• val大于当前节点的值就向右子树走
• val小于当前节点的值就向左子树走
• 直到找到一个空节点就插入

bool insert(T val)
{
	pNode cur = new Node(val);
	pNode root = Root;
	if (Root!=nullptr&&find(val) != nullptr)
	{
		return false;
	}
	if (root == nullptr)
	{
		Root = cur;
		return true;
	}

	while (root != nullptr)
	{
		if (val > root->_data)
		{
			if (root->_right == nullptr)
			{
				root->_right = cur;
				break;
			}
			root = root->_right;
		}
		else if (val < root->_data)
		{
			if (root->_left == nullptr)
			{
				root->_left = cur;
				break;
			}
			root = root->_left;
		}
	
	}
	return true;
}

二叉搜索树的删除

二叉搜索树的删除是最难的，需要分情况说明。

• 左子树为空，但右子树不为空
• 右子树为空，但左子树不为空
• 左右都为空
• 左右都不为空

对于最后一种情况来说，这个节点是一个叶子节点，可以直接删除。

右为空左不为空

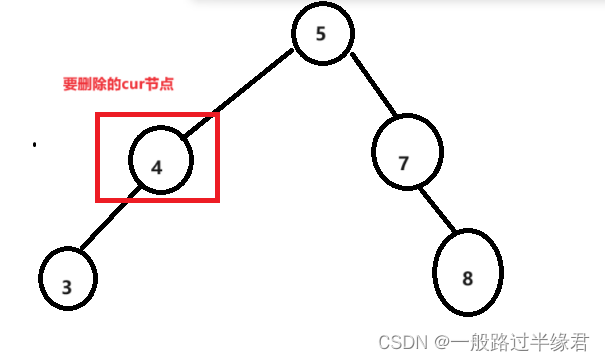
当 cur 节点是父节点的左子树，就需要将父节点的左向量连接在cur节点的左子树上。

????????

反之当cur节点是父节点的右子树，就需要将父节点的右向量连接在cur节点的左子树上。

左为空右不为空

若cur节点的左子树为空，且cur节点是父节点的左子树，就需要将父节点的左向量连接在cur节点的右子树上。

若cur节点是父节点的右子树，则需要将父节点的右向量连接在cur节点的右子树上。

左右不为空?

若节点的左右子树都不是空树，为了不破坏二叉搜索树的结构，就需要利用一个中间变量(minright)来辅助删除。

minright应是被删节点的右子树中的最左节点。

1：若minright是被删节点的右节点。

这种情况下就直接交换cur和minright 的值，然后让cur 的右指针指向 minright 的右节点。

2：minright不是被删节点的右节点。

?

这种情况下，就需要记录 minright 的 parent 节点，让 parent 的左指针指向 minright 的右节点。

然后再交换 cur 和 minright 的值，再删除 minright 的节点。

	bool erase(T val)
	{
		pNode cur = Root;
		pNode parent = nullptr;
		while (cur != nullptr)
		{
			//大于向右走
			if (val > cur->_data)
			{
				parent = cur;
				cur = cur->_right;
			}
			//小于向左走
			else if (val < cur->_data)
			{
				parent = cur;
				cur = cur->_left;
			}
			//等于则开始消除
			else
			{
				if (cur->_right == nullptr)
				{
					//如果是根节点，就直接拿左节点当根
					if (cur == Root)
					{
						Root = cur->_left;

					}
					//否则就正常进行
					else
					{
						//如果cur是parent的右节点，就直接拿cur的左节点和parent的右节点相连
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						//如果cur是parent的左节点，就拿cur的左节点和parent的左节点相连
						else if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
					}
					delete cur;
				}
				else if (cur->_left == nullptr)
				{
					//如果是根节点
					if (cur == Root)
					{
						Root = cur->_right;
					}
					//否则就正常进行
					else
					{
						//如果cur是parent的右节点，就直接拿cur的左节点和parent的右节点相连
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						//如果cur是parent的左节点，就拿cur的左节点和parent的左节点相连
						else if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
					}
					delete cur;
				}
				//左右都不为空
				else
				{
					pNode minright = cur->_right;
					parent = cur;
					while (minright->_left)
					{
						parent = minright;
						minright = minright->_left;
					}
					cur->_data = minright->_data;
					if (minright == parent->_right)
					{
						parent->_right = minright->_right;
					}
					else
					{
						parent->_left = minright->_right;
					}
					delete minright;
				}
				return true;
			}
			
		}
		return false;
	}

?

完整代码

using namespace std;
template<class T>
class BSTNode {
public:
	BSTNode(T data)
		:_left(nullptr),_right(nullptr),_data(data)
	{
	}
	T _data;
	BSTNode<T>* _left;
	BSTNode<T>* _right;
};

template<class T>
class BSTree {
	typedef BSTNode<T> Node;
	typedef Node* pNode;
public:
	BSTree()
		:Root(nullptr)
	{}

	~BSTree()
	{
		destroy(Root);
	}
	void destroy(pNode root)
	{
		if (root->_left != nullptr)
		{
			destroy(root->_left);
		}
		if (root->_right != nullptr)
		{
			destroy(root->_right);
		}
		delete(root);
	}

	pNode find(const T& val)
	{
		pNode cur = Root;
		if (cur->_data == val)
		{
			return cur;
		}
		while (cur != nullptr)
		{
			if (val > cur->_data)
			{
				cur = cur->_right;
			}
			else if (val < cur->_data)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}
	bool erase(T val)
	{
		pNode cur = Root;
		pNode parent = nullptr;
		while (cur != nullptr)
		{
			//大于向右走
			if (val > cur->_data)
			{
				parent = cur;
				cur = cur->_right;
			}
			//小于向左走
			else if (val < cur->_data)
			{
				parent = cur;
				cur = cur->_left;
			}
			//等于则开始消除
			else
			{
				if (cur->_right == nullptr)
				{
					//如果是根节点，就直接拿左节点当根
					if (cur == Root)
					{
						Root = cur->_left;

					}
					//否则就正常进行
					else
					{
						//如果cur是parent的右节点，就直接拿cur的左节点和parent的右节点相连
						if (cur == parent->_right)
						{
							parent->_right = cur->_left;
						}
						//如果cur是parent的左节点，就拿cur的左节点和parent的左节点相连
						else if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
					}
					delete cur;
				}
				else if (cur->_left == nullptr)
				{
					//如果是根节点
					if (cur == Root)
					{
						Root = cur->_right;
					}
					//否则就正常进行
					else
					{
						//如果cur是parent的右节点，就直接拿cur的左节点和parent的右节点相连
						if (cur == parent->_right)
						{
							parent->_right = cur->_right;
						}
						//如果cur是parent的左节点，就拿cur的左节点和parent的左节点相连
						else if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
					}
					delete cur;
				}
				//左右都不为空
				else
				{
					pNode minright = cur->_right;
					parent = cur;
					while (minright->_left)
					{
						parent = minright;
						minright = minright->_left;
					}
					cur->_data = minright->_data;
					if (minright == parent->_right)
					{
						parent->_right = minright->_right;
					}
					else
					{
						parent->_left = minright->_right;
					}
					delete minright;
				}
				return true;
			}
			
		}
		return false;
	}
	bool insert(T val)
	{
		pNode cur = new Node(val);
		pNode root = Root;
		if (Root!=nullptr&&find(val) != nullptr)
		{
			return false;
		}
		if (root == nullptr)
		{
			Root = cur;
			return true;
		}

		while (root != nullptr)
		{
			if (val > root->_data)
			{
				if (root->_right == nullptr)
				{
					root->_right = cur;
					break;
				}
				root = root->_right;
			}
			else if (val < root->_data)
			{
				if (root->_left == nullptr)
				{
					root->_left = cur;
					break;
				}
				root = root->_left;
			}
		
		}
		return true;
	}
private:
	pNode Root;
};

总结

二叉搜索树是一种进阶版的二叉树结构，实际应用中十分广泛，面试题中经常出现，而在二叉搜索树之上还有AVL树和红黑树，不过这些都是后话了。