2024 电子科技大学 《820 计算机专业基础》真题及解析（更新中...）

数据结构算法题（15 分，8 + 7）?

1. 比较一棵二叉树的终端节点到根节点的路径长度，路径长度为关键字之和，输出路径长度最短的终端节点。

? ??输入：第一行输入一个整数 n, 表示结点的个数，第二行输入二叉树的中序遍历序列，第三行输入二叉树的后序遍历序列。

? ? 输出：路径长度最短的叶子节点的关键字。

? ? 用例：

? ? 输入：

????7

? ? 3 2 1 4 5 7 6

? ? 3 1 2 5 6 7 4

? ? 输出：

? ? 1

示例代码?

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点结构
struct TreeNode {
    int key;
    struct TreeNode *left;
    struct TreeNode *right;
};

// 构建二叉树
static struct TreeNode *BuildTree(int *inorder, int *postorder, int inStart, int inEnd, int postStart, int postEnd)
{
    // 终止条件：中序遍历或后序遍历的起始位置超过结束位置
    if ((inStart > inEnd) || (postStart > postEnd)) {
        return NULL;
    }

    // 创建根节点
    struct TreeNode *root = (struct TreeNode *)malloc(sizeof(struct TreeNode));
    if (!root) {
        return NULL; // 内存分配失败
    }

    // 根据后序遍历确定根节点值
    root->key = postorder[postEnd];

    // 在中序遍历中找到根节点的位置
    int rootIndex;
    for (rootIndex = inStart; rootIndex <= inEnd; ++rootIndex) {
        if (inorder[rootIndex] == root->key) {
            break;
        }
    }

    // 计算左子树和右子树的节点数量
    int leftSize = rootIndex - inStart;
    int rightSize = inEnd - rootIndex;

    // 递归构建左子树和右子树
    root->left = BuildTree(inorder, postorder, inStart, rootIndex - 1, postStart, postStart + leftSize - 1);
    root->right = BuildTree(inorder, postorder, rootIndex + 1, inEnd, postEnd - rightSize, postEnd - 1);

    return root;
}

// 计算从叶子节点到根节点的路径长度
static int CalculatePathLength(struct TreeNode *root)
{
    if (root == NULL) {
        return 0;
    }

    // 递归计算左子树和右子树的路径长度
    int leftPath = CalculatePathLength(root->left);
    int rightPath = CalculatePathLength(root->right);

    // 返回当前节点值与左右子树中较短路径的和
    return root->key + ((leftPath > rightPath) ? rightPath : leftPath);
}

// 找到路径长度最短的终端节点
static void FindShortestPathLeaf(struct TreeNode *root, int *shortestPath, int *shortestLeaf)
{
    if (root == NULL) {
        return;
    }

    // 当前节点为叶子节点时
    if ((root->left == NULL) && (root->right == NULL)) {
        // 计算当前路径长度
        int pathLength = CalculatePathLength(root);

        // 更新最短路径和对应的叶子节点值
        if (*shortestPath == -1 || pathLength < *shortestPath) {
            *shortestPath = pathLength;
            *shortestLeaf = root->key;
        }
    }

    // 递归查找左右子树
    FindShortestPathLeaf(root->left, shortestPath, shortestLeaf);
    FindShortestPathLeaf(root->right, shortestPath, shortestLeaf);
}

int main()
{
    int n;
    printf("Enter the number of nodes: ");
    scanf_s("%d", &n);

    int *inorder = (int *)malloc(n * sizeof(int));
    int *postorder = (int *)malloc(n * sizeof(int));
    if (!inorder || !postorder) {
        return -1; // 内存分配失败
    }

    // 输入中序遍历序列
    printf("Enter the inorder traversal sequence: ");
    for (int i = 0; i < n; ++i) {
        scanf_s("%d", &inorder[i]);
    }

    // 输入后序遍历序列
    printf("Enter the postorder traversal sequence: ");
    for (int i = 0; i < n; ++i) {
        scanf_s("%d", &postorder[i]);
    }

    // 构建二叉树
    struct TreeNode *root = BuildTree(inorder, postorder, 0, n - 1, 0, n - 1);

    int shortestPath = -1;
    int shortestLeaf = -1;

    // 寻找路径长度最短的终端节点
    FindShortestPathLeaf(root, &shortestPath, &shortestLeaf);

    // 输出结果
    printf("The terminal node with the shortest path length is: %d\n", shortestLeaf);

    // 释放动态分配的内存
    free(inorder);
    free(postorder);

    return 0;
}

时间复杂度分析：

1. 构建二叉树 (BuildTree 函数)：

   • 在每次递归调用中，都需要在 inorder 数组中找到根节点的位置，这部分的时间复杂度是 O(n)，其中 n 是节点的总数。

   • 总体时间复杂度为 O(n log n)，因为每个节点都需要在中序遍历数组中进行查找。

2. 计算从叶子节点到根节点的路径长度 (CalculatePathLength 函数)：

   • 对于每个节点，都需要递归计算其左右子树的路径长度，总体时间复杂度是 O(n)，其中 n 是节点的总数。

3. 找到路径长度最短的终端节点 (FindShortestPathLeaf 函数)：

   • 在每个终端节点处都需要计算路径长度，总体时间复杂度是 O(n)，其中 n 是节点的总数。

4. 主函数 (main 函数)：

   • 输入数组的读取和动态内存分配的时间复杂度是 O(n)。

   • 最终调用 BuildTree、CalculatePathLength、FindShortestPathLeaf 函数，因此主函数的总体时间复杂度是 O(n log n)。

总体时间复杂度： O(n log n)

空间复杂度分析：

1. 递归栈空间 (BuildTree 函数)：

   • 由于是递归实现，每次递归调用都需要在栈上保存当前递归状态。最坏情况下，递归栈的深度是二叉树的高度，而二叉树的高度最坏情况下可以达到 n（每个节点只有一个子节点形成的斜树）。因此，递归栈空间的最坏情况空间复杂度是 O(n)。

2. 递归栈空间 (CalculatePathLength 函数)：

   • 由于是递归实现，每次递归调用都需要在栈上保存当前递归状态。最坏情况下，递归栈的深度是二叉树的高度，而二叉树的高度最坏情况下可以达到 n。因此，递归栈空间的最坏情况空间复杂度是 O(n)。

3. 递归栈空间 (FindShortestPathLeaf 函数)：

   • 由于是递归实现，每次递归调用都需要在栈上保存当前递归状态。最坏情况下，递归栈的深度是二叉树的高度，而二叉树的高度最坏情况下可以达到 n。因此，递归栈空间的最坏情况空间复杂度是 O(n)。

4. 动态分配的堆空间：

   • 每个节点都需要动态分配内存，总体空间复杂度是 O(n)，其中 n 是节点的总数。

5. 其他变量和数组：

   • 除递归栈和动态分配的堆空间外，程序中使用了一些整型变量和输入数组。这部分的空间复杂度是 O(1)。

总体空间复杂度： O(n)

输出示例

2. 在 n 个数中查询 k 个指定的数（要求最少存储）

示例代码

#include <stdio.h>
#include <stdlib.h>

// 交换数组中两个元素的值
static void Swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 最小堆调整
static void Heapify(int arr[], int n, int i)
{
    int largest = i;    // 初始化最大值为根节点
    int left = 2 * i + 1;   // 左子节点
    int right = 2 * i + 2;  // 右子节点

    // 如果左子节点大于根节点
    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }

    // 如果右子节点大于最大值
    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }

    // 如果最大值不是根节点
    if (largest != i) {
        Swap(&arr[i], &arr[largest]);

        // 递归调整受影响的子树
        Heapify(arr, n, largest);
    }
}

// 构建最小堆
static void BuildHeap(int arr[], int n)
{
    // 构建堆（重新排列数组）
    for (int i = n / 2 - 1; i >= 0; i--) {
        Heapify(arr, n, i);
    }
}

// 堆排序
static void HeapSort(int arr[], int n)
{
    // 构建最大堆
    BuildHeap(arr, n);

    // 依次从堆中取出元素
    for (int i = n - 1; i > 0; i--) {
        // 将当前根节点移至末尾
        Swap(&arr[0], &arr[i]);

        // 在减小的堆上调用最大堆调整
        Heapify(arr, i, 0);
    }
}

// 二分查找
static int BinarySearch(int *array, int low, int high, int target)
{
    while (low <= high) {
        int mid = low + (high - low) / 2;
        if (array[mid] == target) {
            return mid + 1; // 位置从1开始
        } else if (array[mid] < target) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }

    return 0; // 未找到
}

int main()
{
    int n;

    // 输入 n
    printf("Enter the number of elements (n): ");
    scanf_s("%d", &n);

    // 输入 n 个数
    printf("Enter %d numbers:\n", n);
    int *array = (int *)malloc(n * sizeof(int));
    if (array == NULL) {
        fprintf(stderr, "Memory allocation failed\n");
        return 1;
    }

    for (int i = 0; i < n; i++) {
        scanf_s("%d", &array[i]);
    }

    // 使用最小堆排序
    HeapSort(array, n);

    // 输出排序后的数组
    printf("Sorted array:\n");
    for (int i = 0; i < n; i++) {
        printf("%d ", array[i]);
    }

    // 输入 k
    int k;
    printf("\nEnter the number of elements to search (k): ");
    scanf_s("%d", &k);

    // 输入 k 个数
    printf("Enter %d numbers to search:\n", k);
    for (int i = 0; i < k; i++) {
        int searchNumber;
        scanf_s("%d", &searchNumber);

        // 使用二分查找在有序数组中查找位置
        int position = BinarySearch(array, 0, n - 1, searchNumber);
        if (position) {
            printf("%d ", position);
        } else {
            printf("Not Found ");
        }
    }

    // 释放动态分配的内存
    free(array);

    return 0;
}

时间复杂度分析：

1. 堆排序的时间复杂度：

   • 构建堆： 时间复杂度为 O(n)。对每个非叶子节点进行堆调整，而非叶子节点的数量是 n/2，其中 n 是元素的总数。

   • 排序： 每次将最大值放到数组末尾，然后对剩余的部分进行堆调整。堆调整的时间复杂度是 O(log n)，而总共需要进行 n 次调整。因此，排序的时间复杂度为 O(n log n)。

   综合起来，堆排序的时间复杂度为 O(n + n log n) = O(n log n)。

2. 二分查找的时间复杂度： 二分查找的时间复杂度为 O(k log n)，其中 n 是数组的长度，k 是要搜索的元素数量。每一次都将搜索范围缩小一半，直到找到目标值或者搜索范围为空。由于 k <= n，可以将其表示为 O(n log n)。

综合起来，整个程序的时间复杂度主要由堆排序决定，为 O(n log n)。

空间复杂度分析：

1. 堆排序的空间复杂度： 堆排序是原地排序算法，不需要额外的空间来存储数据结构，只需要常数级别的辅助空间。因此，堆排序的空间复杂度为O(1)。

2. 二分查找的空间复杂度： 二分查找的空间复杂度也是常数级别的，为O(1)。

3. 输入数组的空间复杂度： 在堆排序前，程序使用了一个大小为 n 的整数数组 (array) 来存储输入的 n 个数。因此，这部分的空间复杂度为 O(n)。

4. 其他变量的空间复杂度： 除了输入数组外，程序使用了一些常数级别的辅助变量，如循环中的索引和临时变量。这些额外变量的空间复杂度可以被认为是 O(1)。

综合起来，整个程序的空间复杂度为 O(n)，其中 n 是输入的数组大小。

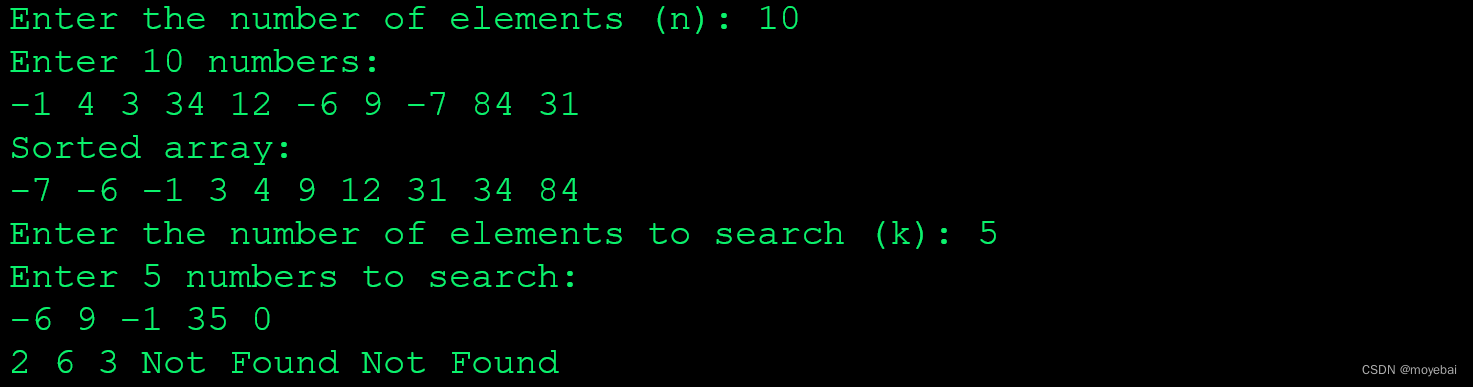
输出示例