左数效应 整数关口与光的折射

常常有人问，新的因子/策略从哪里来？今天的笔记或许能启发你的思路。

从1932年起，研究人员就注意到以9结尾的价格（比如$3.99），在消费者的认知中，要远远小于邻近的整数价格（$4.00）。后来这一效应被称为 left-digit effect。在证券交易中，类似的情况一样存在，不过它的表现形式是整数关口压力。

---

左数效应

关于 Left-digit effect 是否真实存在，以及如何解释和运用，经济学家/心理学家们一直研究到现在。

我看到的最近的研究直到 2023 年 2 月，John A. List（来自鼎鼎大名的芝加哥大学经济系） 等人对 Lyft 的定价体系进行了研究（《Left-Digit Bias at Lyft》），指出如果他们利用 left-digit dias 来进行定价的话，大约每年可以增加 1.6 亿美元的利润。

来自康纳尔的 Manoj Thomas 和来自纽约大学的 Vicki Morwitz 在 2005 年的《消费者研究杂志》上，发表了《Penny Wise and Pound Foolish: The Left-Digit Effect in Price Cognition》（小事聪明，大事愚蠢：价格认知中的左数效应》，被引用 300 余次，应该是这个领域比较有影响力的文献了，对这一现象进行了建模研究，确认了这一现象存在，并解释了与之相关的认知现象。

证券交易中的整数关口

我们更关注这一现象及其伴生现象在证券交易中的表现。

1991 年， 南加州大学的 Lawrence Harris 就研究了证券交易中的类似现象（《Stock Price Clustering and Discreteness》），但他是从交易价格的聚类与离散的角度来进行分析和立论的。

---

他的结论是，股票价格聚集在整数分数上。价格水平和波动增加时，价格簇的个数就会增加。不过，当时美股交易的最小单位是 1/8 美金，从 2001年1月29日起，纽交所取消了之前的 1/8,1/16 交易限制，全部改为十进制小数。所以，关于股票价格聚集的研究现在来看，就应该有了新的结论。

在证券交易中，价格定价机制与零售不太一样。后者要充分利用左数效应，让消费者有占了便宜的感觉。但证券价格定价更类似于房地产这种一货一价的交易，它的价格取决于双方谈判。

谈判的双方地位对等，并且由于认知原因，于是都倾向于使用整数价格。比如，一幢房子的主体价格，定在 500 万是合适的，510 万也是合适的，但如果要定为 513.2 万元，反倒会导致双方在这个价格细节上进行过多的纠缠，导致更难成交。

在证券交易中也是如此。交易者更希望以整数买入股票，再以整数卖出，这样更方便记忆和计算利润。如此以来，由于在整数关口可能聚集大量的委单，因而它就有了压力和支撑的作用。

---

在 A 股，指数上会有一些著名的整数关口，比如 3000 点；我们会说 A 股万年的 3000 点，即使实际上 A 股的波动中枢可能是 31xx 点或者 29xx 点，我们仍然会这么说。

在这个点位上下，每隔 100 点都是一个大的整数压力/支撑位。如果在这个节点上遇到其它技术指标共振，那么压力/支撑成立的可能性就更大。一旦得到确认，后续趋势也会大一些、久一些。

在个股上，20 元以下的个股，每个以 1 元为结尾的数字都显然是整数关口，此外在一些低价股上，每个以 0.1 元结尾的数字都是整数产口。对百元股来说，则可能要以 10 元为单位，才能构成整数关口。这方面我们还需要时间去做一些实证研究。

光折射原理预测整数关口后的走势

这是最近读到的一篇论文，运用光折射原理来分析股价走势在整数产口的行为，脑洞比较大。不过研究确实也要持有开放的心态，才容易有意想不到的结果。

首先我们回顾一下光在两种不同密度的物质中传播时的行为。当光在接触到两种介质的交界表面时，就会发生部分反射、部分折身的现象。

如果入射角度合适，就会穿过介质，发生折射 – 这可以对应到股价运行到某个区域后，突破了该区间，并且改变了角度；也可能发生完全反射 – 对应着股价无法穿越该区间，导致反弹。

---

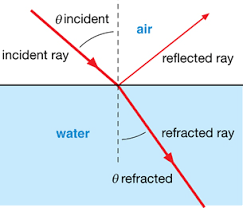
这笔文章把整数关口当成两种不同环境的交界界面（其实更广义来看，这也是密集成交区的一种），然后运用光折射原理，计算出入射角、折射角和折射率。

以育碧为例：

---

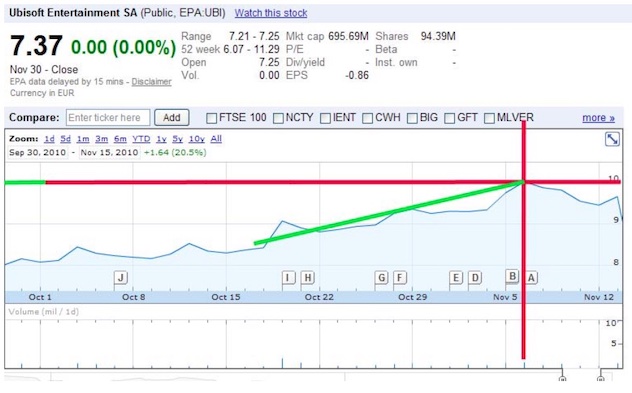
育碧在10月26日达到10元整数关口。相关参数定义如下：

1. 当股价等于整数关口时，确定入射点。
2. 入射线使用入射点前 10 天的收盘价进行线性回归。
3. 入射线与法线之间的夹角记为入射角。
4. 介质 1（整数关口前）的折射率$n_1$假定为 1.
5. 介质 2（整数关口后）的折射率$n_2$