KNN中KD树的查询操作
发布时间:2023年12月26日
1.简介
KD树(K-Dimensional Tree)是一种二叉树,用于在k维空间中对数据进行分割和组织。它具有以下特点:
2.基本知识点:
- KD树是一种二叉树,每个节点代表一个k维向量。
- 每个节点的左子树和右子树分别表示比当前节点小和大的数据。
- KD树的构建过程是通过递归的方式进行的,每次选择一个维度作为切分维度,以该维度的中值作为节点,将数据集切分成两部分。
- 在查询时,通过比较目标向量和节点的切分维度的值,可以确定搜索路径。
3.与平衡二叉树的不同之处:
- 平衡二叉树(如AVL树、红黑树)的主要目的是保持树的左右子树的高度差不超过1,从而提供快速的插入、删除和搜索操作。
- KD树并不一定是平衡的,因为它的构建过程是基于数据集的切分,而不是固定的旋转操作。
- KD树的构建过程是通过选择切分维度和切分值来进行的,因此它可能会导致树的不平衡。
- 不平衡的KD树可能导致搜索操作的效率下降,因为搜索路径可能会非常长。
4.基于上篇博客编写:
需要将上篇博客中的函数进行导入(作者命名为了KDtree.py):
KD树构建链接
5.代码:
这里随机了10000个1到1000的随机整数,输入的点需要自己手动调整(这里设置的是(44, 46),在代码中可以看到)
代码实现了使用KD树进行最近邻搜索的功能。首先,通过随机生成一组坐标点作为输入数据。然后,给定一个预测点predict,代码使用普通方法和KD树两种方式分别找到距离预测点最近的点,并计算出最近距离。
具体流程如下:
- 创建了一个KD树,将输入的数据作为构建KD树的节点。
- 使用普通方法,通过计算每个点到预测点的欧几里得距离,对输入数据进行排序,找到距离最近的点。
- 使用KD树方法,通过建立的KD树结构,从根节点开始,按照预测点的坐标与节点的划分维度进行比较,逐步向下搜索,直到找到最近的叶子节点。
- 在搜索过程中,通过维护一个栈来记录搜索路径,以便在回溯时处理另一侧的节点。
- 最后,输出普通方法和KD树方法分别找到的最近点及其距离,并输出两种方法的执行时间。
from KDtree import *
import math
import random
import time
def append_stack(node, predict, stack):
loop_num = 0
stack.append(node.data + (0,))
while node.rchild != None or node.lchild != None:
tup = None
if predict[loop_num % 2] < node.data[loop_num % 2]:
if node.lchild == None:
break
node = node.lchild
tup = (-1,)
else:
if node.rchild == None:
break
node = node.rchild
tup = (1,)
stack.append(node.data + tup)
loop_num += 1
def search(root, predict, stack):
min_distance = 1000
min_node = None
while True:
up_node = root
distance = math.sqrt(pow((stack[-1][0] - predict[0]), 2) + pow((stack[-1][1] - predict[1]), 2))
if distance < min_distance:
min_distance = distance
min_node = stack[-1]
# 移除这个点
last = stack[-1][2]
stack.pop()
if stack == []:
break
# 下一个点用来比较是否相交,以确定要不要给另一侧的点考虑进去
if min_distance > abs(predict[(len(stack) - 1) % 2] - stack[-1][(len(stack) - 1) % 2]):
# 得到最后一个点的位置
for _, _, k in stack[1:]:
if k == -1:
up_node = up_node.lchild
if k == 1:
up_node = up_node.rchild
if last == -1 and up_node.rchild != None:
append_stack(up_node.rchild, predict, stack)
if last == 1 and up_node.lchild != None:
append_stack(up_node.lchild, predict, stack)
return min_node
if __name__ == "__main__":
list_data = [(random.randint(1, 1000), random.randint(1, 1000)) for _ in range(10000)] # 输入数据
predict = (44, 46)
# ----------普通办法-----------
time_start = time.time() # 记录开始时间
# ++++核心代码++++
list_data1 = sorted(list_data, key=lambda x: math.sqrt(pow((predict[0] - x[0]), 2) + pow((predict[1] - x[1]), 2)))
# ++++核心代码++++
print(list_data1[0])
print(math.sqrt(pow((list_data1[0][0] - predict[0]), 2) + pow((list_data1[0][1] - predict[1]), 2)))
time_end = time.time() # 记录结束时间
time_sum = time_end - time_start # 计算的时间差为程序的执行时间,单位为秒/s
print('time_sum1: ', time_sum)
# ----------------------------
print('**************************************')
# ----------KD树办法-----------
time_start = time.time() # 记录开始时间
# ++++核心代码++++
root = create(list_data) #创建KD树
# ++++核心代码++++
time_end = time.time() # 记录结束时间
time_sum = time_end - time_start # 计算的时间差为程序的执行时间,单位为秒/s
print('time_sum2.1: ', time_sum)
time_start = time.time() # 记录开始时间
# ++++核心代码++++
stack = []
append_stack(root, predict, stack)
list_data2 = search(root, predict, stack)
# ++++核心代码++++
print(list_data2)
print(math.sqrt(pow((list_data2[0] - predict[0]), 2) + pow((list_data2[1] - predict[1]), 2)))
time_end = time.time() # 记录结束时间
time_sum = time_end - time_start # 计算的时间差为程序的执行时间,单位为秒/s
print('time_sum2.2: ', time_sum)
# ----------------------------
6.效果:
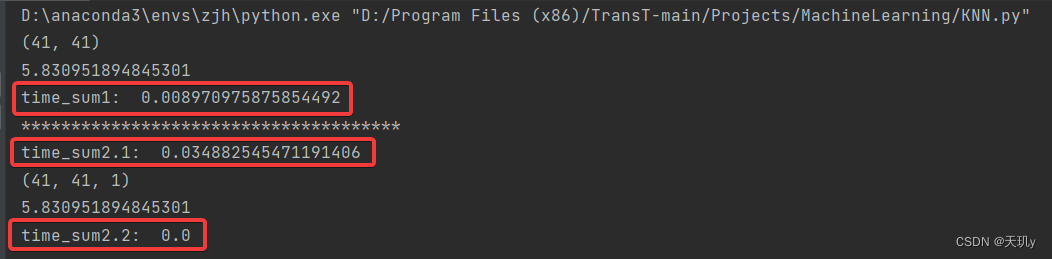
- time_sum1代表通过排序得到最邻近点需要的时间
- time_sum2.1代表构建KD树需要的时间
- time_sum2.1代表通过KD树查询得到最邻近点需要的时间
确实,构造KD树会比较浪费时间,但是通过KD树查询需要的时间几乎为0
小结:
关注我给大家分享更多有趣的知识,以下是个人公众号,提供 ||代码兼职|| ||代码问题求解||
由于本号流量还不足以发表推广,搜我的公众号即可:
文章来源:https://blog.csdn.net/m0_72249799/article/details/135229639
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Postman接口测试之Post、Get请求方法
- 室外防水款蓝牙信标
- JDK8终将走进历史,Oracle宣布JDK继续免费
- HTML标签
- Kyligence 发布数据和分析领域垂直大模型司南(Compass)
- Linux目录切换相关命令( cd命令和pwd命令)
- [Angular] 笔记 22:ElementRef
- antdesign mobile 实现点击弹form弹窗
- Golang - 主线程让子线程退出的三种方式
- lombok 相关注解