Support Vector Machine(SVM)——支持向量机
1.从逻辑回归到SVM
? ? ? ? 回顾一下逻辑回归的模型
????????????????
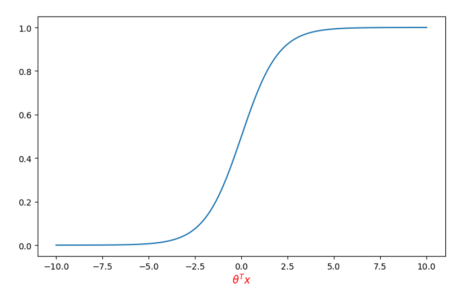
? ? ? ? 然后经过sigmoid函数得到预测y=1的概率,sigmoid函数如下图
????????????????
? ? ? ? 对于单个样本来说损失函数如下
????????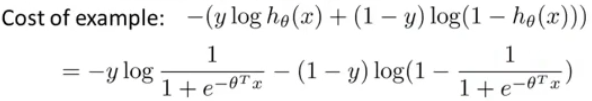 ??
??
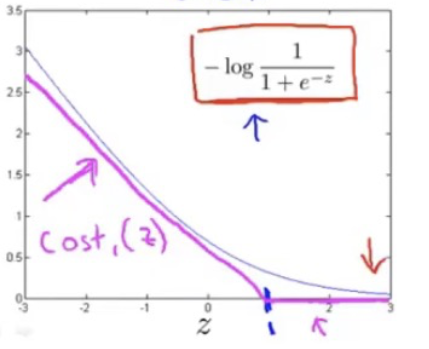
? ? ? ? 当一个输入的真实标签为1时,损失函数就只剩,如左图所示,我们想要让
,来使损失函数尽可能的小
? ? ? ? 对于SVM来说,损失函数会做些修改,如右图所示,是一个分段函数,在>=1的时候,损失值直接为0,而<1部分是一条线段,假设命名为。
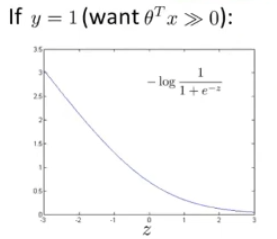 ????????
????????
???????当一个输入的真实标签为0时,损失函数就只剩,如左图所示,同时我们想要让
,来使损失函数尽可能的小
? ? ? ?同样的修改方式,在<=1的时候,损失值直接为0,而>1部分是一条线段,假设命名为。
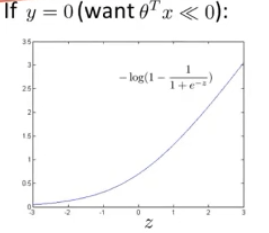

? ? ? ? 于是在逻辑回归的基础上,我们可以得到SVM的损失函数如下
????????
对比逻辑回归,除了cost部分外,还有如下不同
- 省去了
,因为这并不会影响
的最优取值,只是影响函数值而已
- 令C=
,接着正则化方式从
到
? ? ? ? 最后有别于逻辑回归经过一个sigmoid输出概率,SVM在得到参数的值后,直接进行预测????????????????????????
????????????????????????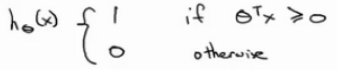
2.SVM——大间距分类器
? ? ? ? SVM构造出的决策边界总是使决策边界到两类样本点的距离较大,这点有别于感知机。
2.1 直观的理解
? ? ? ? 回顾一下SVM修改后的损失函数
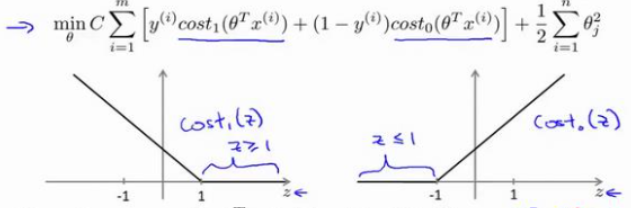
? ? ? ? 如果说有一个y=1的正样本,如果,预测值就为1,预测正确。但如果从损失函数的来看,只有当
的时候,损失函数的值才为0,同时在训练的过程中为了使损失函数最小,也确实会让
(负样本同理)。也就是说SVM的损失函数让其对分类的要求更高,也就是大间距。
? ? ? ? 接着,我们加上考虑C的影响。如果将C设置成一个非常大的值,则在最小化损失函数的时候,会迫切的希望找到一个让第一项(如下)为0的解,也就是(正样本时)
????????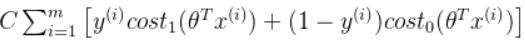
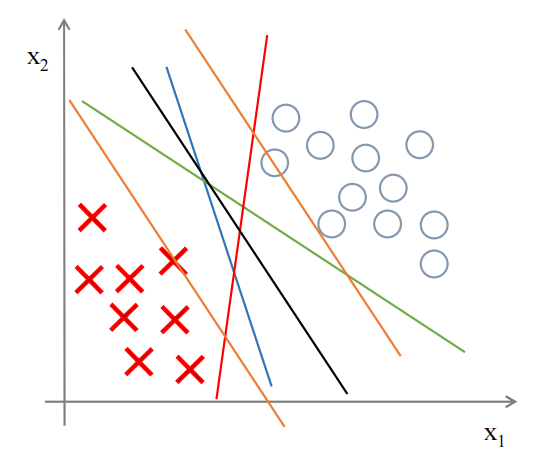
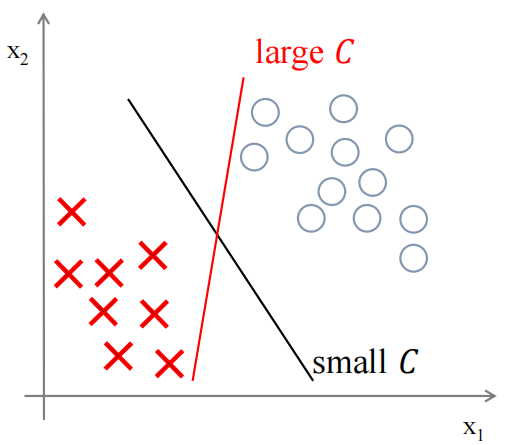
? ? ? ? 对于二分类来说,绿色、蓝色、红色的线都可以将两者分类,但对于SVM来说,黑色的线才是其所要寻找的决策边界,因为它距离两个样本有更大的间隔,从效果上来看,黑色也确实是最好的
????????
? ? ? ? 如果找到了这个,那么可以简化为如下
? ? ? ??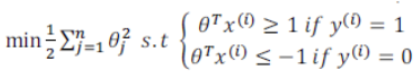
………………………………………………………………………………………………………………
? ? ? ? 额外的对于参数C的理解,在上面的解释中我们使用了一个很大C来举例。因为C=1/λ,所以作用是类似
????????????????????????????????????????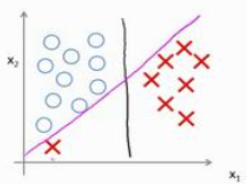
? ? ? ? 但很大的C也意味着,如果多了一个左下角的“x”(有可能是异常值),决策边界直接从黑色的线变成粉色的线,这是不太好的,尽管在SVM中C的取值确实会比较大。如果C设置的不要太大,你仍然会得到和黑色线类似的线,只是分类的结果允许有点错误,忽略掉一些异常点的影响,同时如果你的数据是线性不可分的,也能给出好的结果
????????????????????????????????????????
…………………………………………………………………………………………………………………
2.2 从数学上理解
? ? ? ? 范数,表示向量的长度或大小(模其实是一样的)
????????为了便于理解和画图,假设(即决策边界截距为0),并且特征数n=2
?
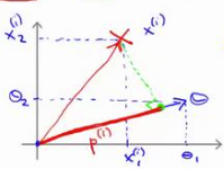
? ? ? ? 设向量与向量
的夹角为t,
为向量
在向量
方向上的投影的长度
=
(向量内积)
???????????????????????????????????????????????
? ? ? ? 假如我们的决策边界是这条黑线,那么θ向量就是与黑线垂直的向量(法向量)
??????????????????????????????????????
? ? ? ? 如果决策边界是这样的,这个间隔更大,同时P也更加的大
?????????????????????????????????????????????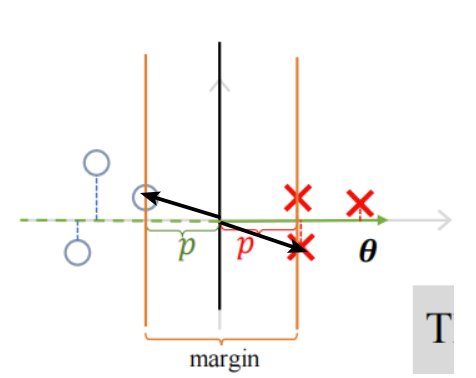
? ? ? ? SVM需要在最小化||θ||的同时,还需要满足
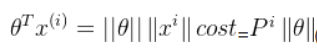
? ? ? ? 那么在最小化||θ||让P更加的大,才能满足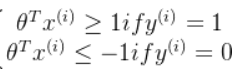 ,由上面两幅图可以分析出,这等价于让样本点距离决策边界距离更加的大
,由上面两幅图可以分析出,这等价于让样本点距离决策边界距离更加的大
? ? ??????????????????????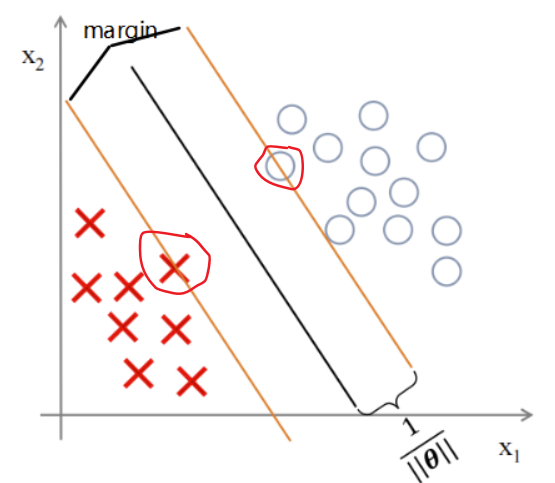
? ? ? ? 间隔大小为,那些则最靠近分类决策面的点,是最难分类的数据点(落在margin线上的)也叫支持向量(support vectors),
2.3 kernel——核函数
? ? ? ? 在之前,为了拟合非线性的数据,我们可以创造高次方的特征,使用多项式回归。
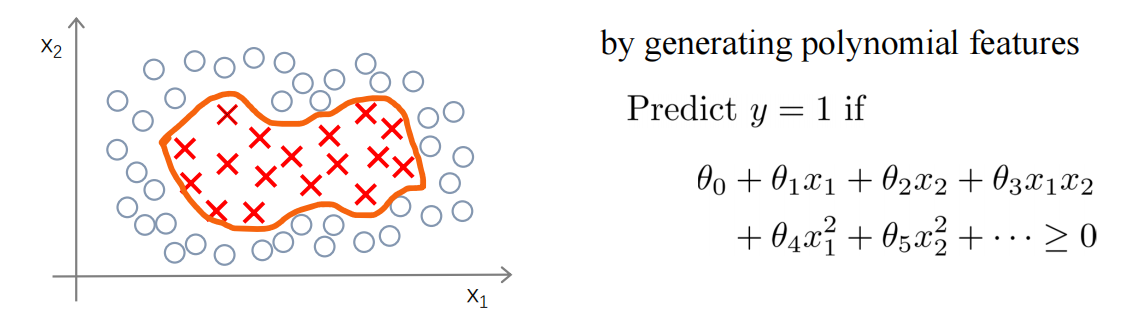
????????而在SVM我们可以使用核函数,不使用核函数的SVM也叫使用线性核函数的SVM。
2.3.1?Gaussian Kernel高斯核函数
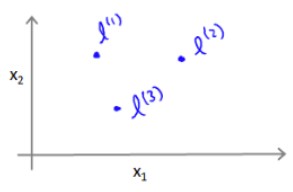
?????????假设我们预先选定了三个地标(lanmarks),输入x通过与计算与这三个地标的近似程度来获得新的特征
????????????????????????????????????????????????????????????????????
????????
????????
????????
其中就是高斯核函数,
表示x与l的距离的平方
? ? ? ? 于是就可以得到
??????????????????????
? ? ? ?假设输入x与某个地标l的距离为0,那么新特征,如果较远,那么f的值就靠近于0
? ? ? ? 下面通过一个示例,看看高斯核函数的转换
? ? ? ??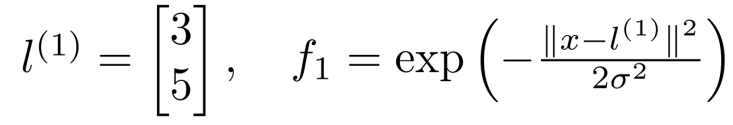
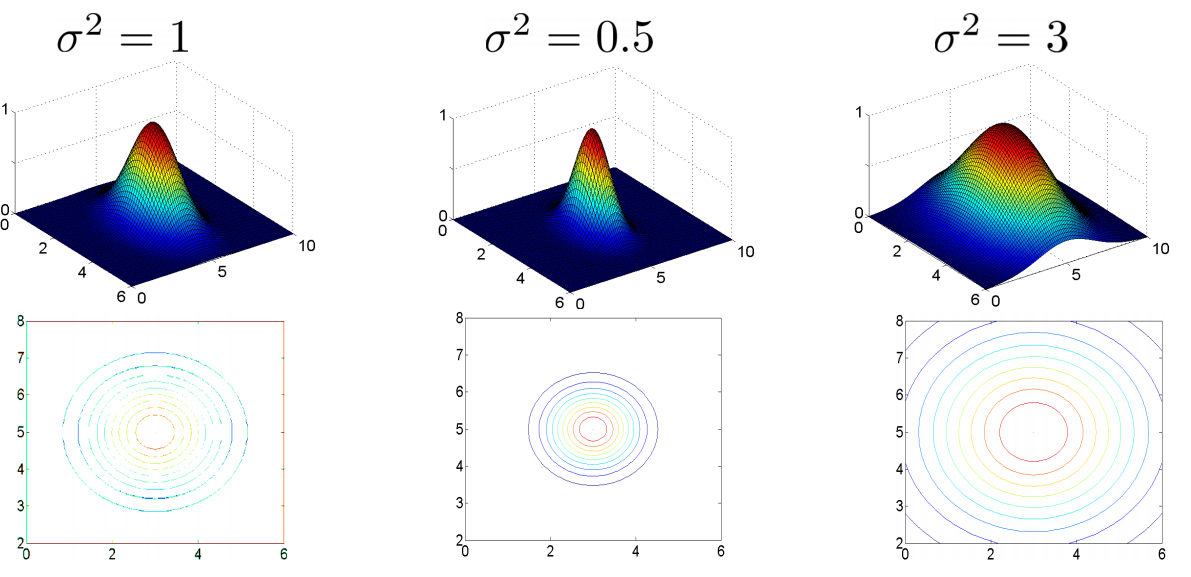
????????图中水平面的坐标为x1,x2而垂直坐标轴代表f。可以看出,只有当x与重合时f才具有最大值。随着x的改变f值改变的速率受到
的控制。
? ? ? ? 只有当x=(3,5)与重合时,f取得最大值,离
越远,f越小。
? ? ? ? 可以看作正态分布的三维形式,因为这个这个式子和正态分布是一样的
????????
相当于对称轴,函数在这里取得最大值,
相当于方差,
越大,分布越散,图象越平坦,
越小,分布越集中,图象越在对称轴突出
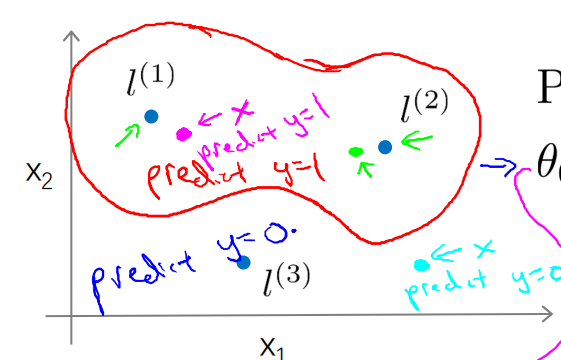
????????在下图中,当实例处于洋红色的点位置处,因为其离更近,但是离
和
较远,因此
接近1,而
接近0,
,因此预测y=1。同理可以求出,对于
离较近的绿色点,也预测y=1,但是对于蓝绿色的点,因为其离三个地标都较远,预测y=0。我们可以得到决策边界类似下图
???????????????????????????????????????????????????????????????????????????
? ? ? ? 这样就可以实现非线性的数据分类。
2.3.2 如何选择地标
? ? ? ? 在SVM会使用所有的训练样本作为地标,假设有m个样本
? ? ? ? 对于每一个样本,都可以计算m个
,得到大小为m的
向量

? ? ? ? 此外还需修改我们的损失函数
???????????????
2.4.3 高斯核函数的超参数
? ? ? ? 超参数为C和
- C较大时,可能会导致低偏差,高方差
- C较小时,可能会导致高偏差,低方差
较大时,可能会导致高偏差,低方差
较小时,可能会导致高偏差,低方差
? ? ? ? 由于高斯核函数会使用每个样本
? ? ? ? 另外使用高斯核函数使用特征缩放是很有必要的
2.5.4 其他Kernel
-
Polynomial kernel
?,包括γ,c,k三个参数
- String kernel
- chi-square kernel
- ???????histogram intersection kernel
- ……
无论什么核函数,都需要满足“Mercer’s Theorem”
????????Mercer条件:训练样本的核矩阵应为半正定矩阵,因为只有所有大于或等于零的特征值才能产生有效的距离???????
2?多分类SVM
????????我们可以利用之前在逻辑回归介绍的一对多方法来解决一个多类分类问题。如果一共有k个类,则我们需要k个模型,以及k个参数向量θ。我们同样也可以训练k个支持向量机来解决多类分类问题。
????????但是大多数支持向量机软件包都有内置的多类分类功能,我们只要直接使用即可。
3 逻辑回归与SVM的选择
n为特征数,m为训练样本数。
????????(1)如果相较于m而言,n要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
????????(2)如果n较小,而且m大小中等,例如n在1-1000之间,而m在10-10000之间,使用高斯核函数的支持向量机。
????????(3)如果n较小,而m较大,例如n在1-1000之间,而m大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
??????????????
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【已解决】namespace “Ui“没有成员 xxx
- 前端笔试题(一)
- JS进阶-作用域、垃圾回收机制、闭包、变量提升(一)
- Python实现API接口并发测试
- 数论:数论分块
- 抖店商家对接带货主播建议,远离头部主播保平安,附沟通话术模板
- SpringBoot 3.1.7 集成Mybatis
- vscode配置Todo Tree插件
- Javascript类型转换方法总结
- FOC系列(四)----重新绘制DRV8301驱动板