基于比较的排序算法总结（java实现版）

发布时间：2023年12月22日

什么是基于比较的排序算法

什么是排序算法的稳定性

基础排序算法的稳定性

什么是基于比较的排序算法

基于比较的排序算法定义：之所以能给元素排序依赖于元素和元素之间的比较，在代码中体现为所处理的数组对应的元素类型实现了Comparable这个接口。

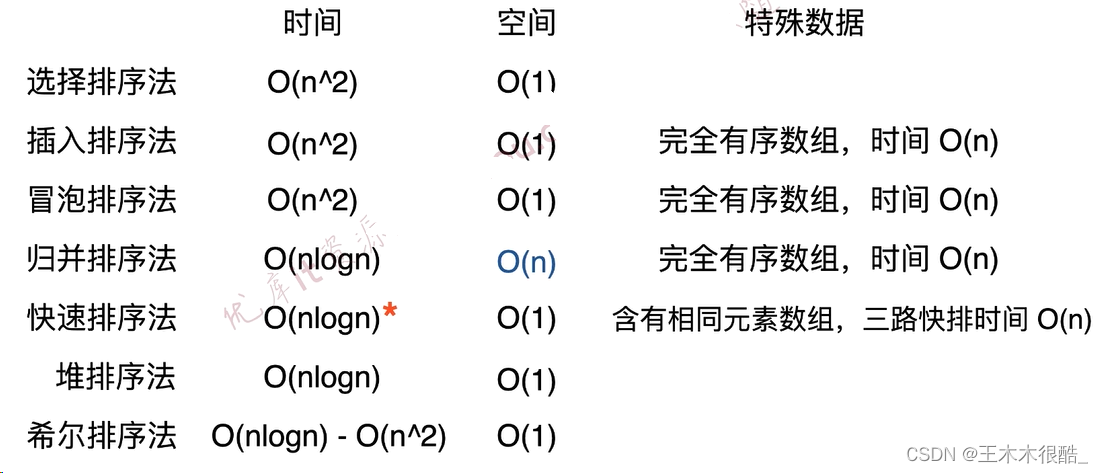
基于比较的排序算法有选择排序、插入排序、冒泡排序、归并排序（自顶向下/自底向上）、快速排序（单/双/三路排序）、堆排序、希尔排序（不同步长序列）。

什么是排序算法的稳定性

排序的稳定性：排序前相等的连个元素在排序后相对位置不变。

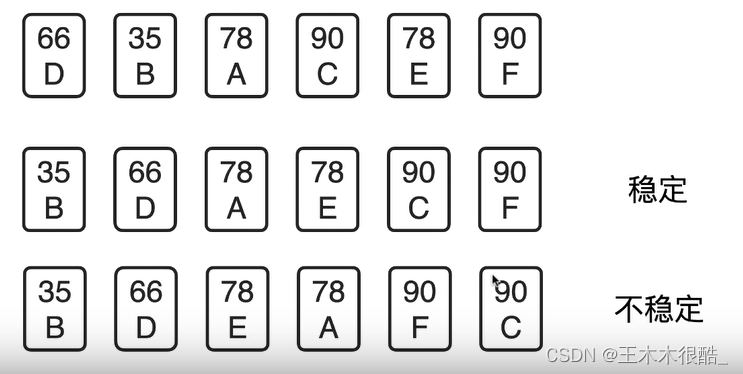
?也就是根据数值大小排序后，A还在E的前面，C也还在F的前面。

基础排序算法的稳定性

选择排序法

按照学生成绩排序，注意A和C的初始位置。

第一趟选择排序后：

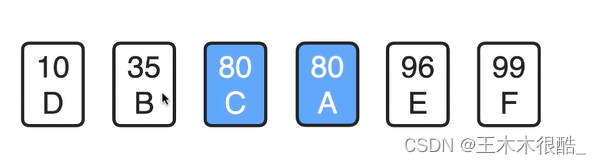
C跑到了A的前面，选择排序算法是不稳定的。?

插入排序法

因为插入排序法从后往前和上一个元素相比时用的是“<?”而不是“<=”，所以对于数值相等的元素不会改变相对位置。所以写代码时要注意有无“=”号，不要错误的实现成不稳定算法。

希尔排序法

希尔排序的分组是隔着元素跳跃的，所以相对位置会改变。

冒泡排序法

因为冒泡排序法每次只比较相邻的元素，，相同大小的元素没有机会“跳跃”。

上图的两个80怎么也没办法交换位置的。但其实它的稳定性也依赖于具体实现，下图标红的是“>”号而不是“>=”号，如果实现的不准确就会变得不稳定。

总结

高级算法的稳定性

快速排序法

快速排序中的portion会随机选择一个点为标准点然后交换位置，这种随机性决定了它是不稳定算法。

堆排序法

堆排序把数组看成了一个树型的结构，树型结构上的两个元素交换位置对应到数组上就会产生跳跃，因此是不稳定的。

举一个小例子：

每次把堆顶的元素放到未处理的最后的一个位置，所以第一步会把AC交换，然后固定下来最大的元素。

即80出堆，C到了堆顶的位置。

归并排序法

我们在merge的过程中如果遇到两个小分数组中有相同的元素，只需要保证优先选择第一个数组中的元素进入新的合并数组中就好，和插入排序和选择排序一样，只要具体实现正确的话，归并排序法是稳定的。

总结

注意

虽然我们花很长的时间来分析各个排序算法的稳定性，但我们需要知道这一切都建立在元素有多个域的前提下，也就是说我们要赋予元素一个额外的意义，比如有两个学生都考了78分，这是属于两个不同的学生的分数，一个域是学生分数，另一个域是学生的名字，而不是说它就单单只是个数字78，在一个纯数字的数组中，两个78根本没有任何区别，稳定性也没有任何意义。?

文章来源:https://blog.csdn.net/xiaoliii0401/article/details/135140171
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！