PYTHON基础:K最邻近算法
K最邻近算法笔记
K最邻近算法既可以用在分类中,也可以用在回归中。在分类的方法,比如说在x-y的坐标轴上又两个成堆的数据集,也就是有两类,如果这个时候有个点在图上,它是属于谁?
原则就是哪一类离它比较近的数据集的点最多,它就是属于谁的。
接下里通过一些简单的例子进行说明。
我们这里要用到的模块叫做scikit_learn,这里面有一些数据可以提供给我进行模拟的,当然也可以使用自己的数据也没问题。
from sklearn.datasets import make_blobs#用于导入模块给好的数据
from sklearn.neighbors import KNeighborsClassifier#KNN分类器
import matplotlib.pyplot as plt #画图工具
from sklearn.model_selection import train_test_split#数据集拆分工具
import numpy as np#数据分析工具
#生成两类两百个点
data=make_blobs(n_samples=200,centers=2,random_state=8)
#数据可视化
X,y =data
#画出数据点图
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
plt.show()
可以在图上绘制出两类的点,如果这个时候放一个点进去,数据这么多肯定没办法一个个计算,我们就可以利用机器学习建立一个模型来判断,这些已知的数据是我们建立模型的基础。我们可不可以直接建立了一个范围,一个点如果在一个范围的内的就是这个属于这个类的
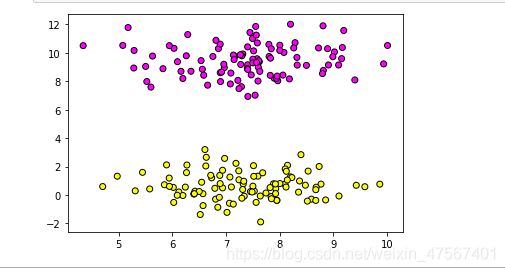
这里就是K最邻近算法建立的“领域范围”了
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np
data=make_blobs(n_samples=200,centers=2,random_state=8)
X,y =data
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
clf=KNeighborsClassifier()
clf.fit(X,y)
#下面是画图
x_min,x_max=X[:, 0].min()-1,X[:, 0].max()+1
y_min,y_max=X[:, 1].min()-1,X[:, 1].max()+1
xx,yy=np.meshgrid(np.arange(x_min,x_max, .02),np.arange(y_min,y_max,.02))
z=clf.predict (np.c_[xx.ravel (),yy.ravel ()])
z=z.reshape(xx.shape)
plt.pcolormesh(xx,yy,z)
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:KNN")
plt.show()
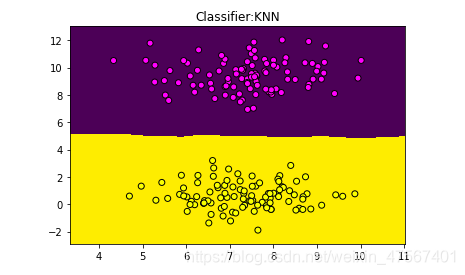
我们输入一点(8.75,4.23)并把它标记为星形,看下可以判定与否
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np
data=make_blobs(n_samples=200,centers=2,random_state=8)
X,y =data
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
clf=KNeighborsClassifier()
clf.fit(X,y)
x_min,x_max=X[:, 0].min()-1,X[:, 0].max()+1
y_min,y_max=X[:, 1].min()-1,X[:, 1].max()+1
xx,yy=np.meshgrid(np.arange(x_min,x_max, .02),np.arange(y_min,y_max,.02))
z=clf.predict (np.c_[xx.ravel (),yy.ravel ()])
z=z.reshape(xx.shape)
plt.pcolormesh(xx,yy,z)
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:KNN")
plt.scatter(8.75,4.23,marker='*',c='red',s=200)
plt.show()
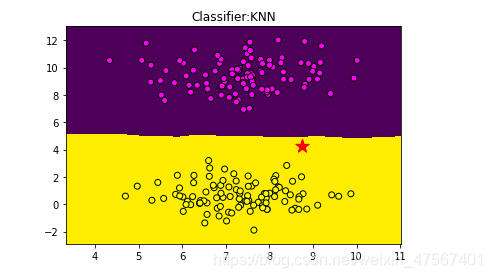
这个时候,我们建立的模型的确得到了准确的表达
那我们再试试一个临界值6.75,4.82
print('\n\n\n')
print('output')
print('===============')
print('new data',clf.predict([[6.75,4.82]]))
print('===============')
print('\n\n\n')
output
===============
new data [1]
===============
分类实在第一类,的确没问题
那我们再来试试多元情况
还是上面一样的代码,我们这个来试试500个数据点并把他们分成五类。
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np
data2=make_blobs(n_samples=500,centers=5,random_state=8)
X2,y2 =data2
plt.scatter(X2[:,0],X2[:,1],c=y2,cmap=plt.cm.spring,edgecolor='k')
生成了下面这个图片

我们在使用和上面一样的算法
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np
data2=make_blobs(n_samples=500,centers=5,random_state=8)
X2,y2 =data2
plt.scatter(X2[:,0],X2[:,1],c=y2,cmap=plt.cm.spring,edgecolor='k')
clf=KNeighborsClassifier()
clf.fit(X2,y2)
x_min,x_max=X2[:, 0].min()-1,X2[:, 0].max()+1
y_min,y_max=X2[:, 1].min()-1,X2[:, 1].max()+1
xx,yy=np.meshgrid(np.arange(x_min,x_max, .02),np.arange(y_min,y_max,.02))
z=clf.predict (np.c_[xx.ravel (),yy.ravel ()])
z=z.reshape(xx.shape)
plt.pcolormesh(xx,yy,z)
plt.scatter(X2[:,0],X2[:,1],c=y2,cmap=plt.cm.spring,edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:KNN")
plt.show()
可见也成功画出了‘范围’
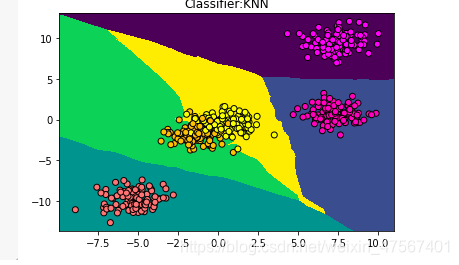
那我们的模拟的准确度有多高呢?用下面这个函数可以计算出来。
print('\n\n\n')
print('output')
print('===============')
print('corrct rate{:.2f}'.format(clf.score(X2,y2)))
print('===============')
print('\n\n\n')
print('\n\n\n')
print('output')
print('===============')
print('corrct rate{:.2f}'.format(clf.score(X2,y2)))
print('===============')
print('\n\n\n')
output
===============
corrct rate0.96
===============
满分1分,这里我们拟合的模型有0.96分,拟合的程度还是相当好的
接下里我们在来看下回归分析的应用
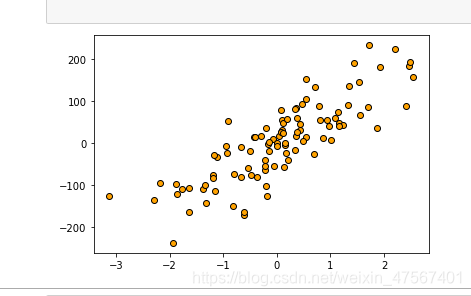
这里我们用make_regression 来生成一个建立模型的数据集
from sklearn.datasets import make_regression#用于生成数据
import matplotlib.pyplot as plt#画图
#一个特征,噪音50
X,y=make_regression(n_features=1,n_informative=1,noise=50,random_state=8)
plt.scatter(X,y,c='orange',edgecolor='k')
plt.show()
我们使用算法开始建立模型
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
#导入KNN回归分析模型
X,y=make_regression(n_features=1,n_informative=1,noise=50,random_state=8)
plt.scatter(X,y,c='orange',edgecolor='k')
reg=KNeighborsRegressor()
#拟合数据
reg.fit(X,y)
z=np.linspace(-3,3,200).reshape(-1,1)
plt.scatter(X,y,c='orange',edgecolor='k')
plt.plot(z,reg.predict(z),c='k',linewidth=3)
plt.title('kNN Regressor')
plt.show()
可以拟合出一条折线
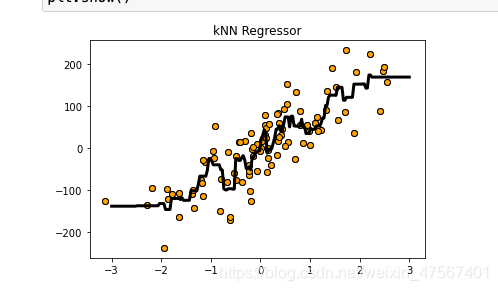
我们来对这个模型进行下测试,看看这个模型好不好使,结果打分是0.77,还是不错的
print('\n\n\n')
print('output')
print('===============')
print('model score{:.2f}'.format(reg.score(X,y)))
print('===============')
print('\n\n\n')
output
===============
model score0.77
===============
参考文献
深入浅出python机器学习–段小手著
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 外卖骑手与行人之间的非零和博弈
- 【已解决】Redis序列化反序列化不一致 - String类型值多了双引号问题
- 吉他初学者学习网站搭建系列(6)——如何根据歌名查歌词
- Linux环境安装MySQL5.7教程
- 常见的网络排错
- 基于 InternLM 和 LangChain 搭建知识库
- 考公什么护眼台灯更推荐?公认好用台灯分享
- Vulnhub-HACKATHONCTF: 2渗透
- 华中科技大学-计算机组成原理-mooc-指令系统
- conda常用命令总结