散射成像相关原理的数学理论推导与证明

发布时间：2023年12月31日

散射技术汇总

1.平面波

2.传输损耗

散射技术汇总

散射成像技术汇总
散射成像技术	先验信息	散射复杂度	利用的光子	FOV	应用场景
利用介质空域特征	波前整形；反馈信号反卷积；PSF 相关性	高	弹道和散射光	受限于记忆效应，小于±3°	磨砂玻璃或者生物组织
大气传输方程	大气散射系数或大气PSF	低	弹道和部分散射光	无限制	雾
传输矩阵标定	完整的传输矩阵	特别高	弹道和散射光	限制于传输矩阵的大小	磨砂玻璃、生物组织等
空域散射光分离	无	中等	只有弹道光子	无限制	雾、浑浊的水、低亮度环境
基于OCT相关的技术	无	特别高	经过多次散射后累积的弹道光	限制于OCT设备	薄生物组织、体内测量
超高时间分辨技术	无	高	只有弹道光子	限制于光源或相机	雾、浑浊的水、纸或者漫反射表面
图像引导成像技术	无	中等	弹道和散射光	待议	磨砂玻璃、生物组织

1.平面波

光的传播是由一个波动方程描述的：

$\nabla^2\Psi(r,t)-\frac{n(r)}{c^2}(\frac{\partial^2\Psi(r,t)}{\partial t^2})=0$

光的电场可以看作波动方程的解：

$\Psi(r,t)=\Psi(r)e^{-i\omega t}$

这个解也可以写成下面这个形式：

$\overline{a}_{n}=a_{n}e^{i\varphi n}$

这个形式包含了两个信息：振幅和相位

在散射介质中，光波沿不同方向传播，具有不同的振幅和相位，它们之间的矢量叠加，通过相干相长与相干相消，就产生了亮暗交替的光学散斑现象。

如果说上公式是散射介质中某个方向分矢量的解，那么最后出射的波解是所有分矢量的合成矢量

$\vec{A}=\dfrac{1}{\sqrt{N}}\sum_{n=1}^{N}a_ne^{i\varphi_n}$

A波矢表示的是n个分矢量的合成矢量。

对构成总矢量的分量向量的统计量采用一些假设，这些假设可以通过考虑合成向量的实部和虚部来理解：?

$R=\operatorname{Re}\left\{A\right\}=\frac{1}{\sqrt{N}}\sum_{n=1}^{N}a_{n}\cos\phi_{n}$

$I=\mathrm{Im}\left\{A\right\}=\frac{1}{\sqrt{N}}\sum_{n=1}^{N}a_{n}\sin\phi_{n}$

2.传输损耗

光子分为弹道光子和散射光子

弹道光子：光线传播中未经散射直接到达传感器的光子，弹道光子单独被传感器采集时，能直接反映目标物或场景的有效信息

散射光子：传播中受到散射影响，传播方向、传播时间相干性等性质发生变化的光子。

实际的散射介质中散射与吸收同时存在

衰减系数： $\beta_t=\beta_{ab}+\beta_{sc}$

平均自由程： $l^*=\frac{1}{\beta_{t}}$

按照比尔-兰伯定律，光在深度为z时的强度 $I(z)=I_0e^{-\frac{z}{l^*}}$

激光穿透散射介质时产生的散斑为菲涅尔型散斑，接收面上的点为散射介质表面上所有散射点源子光波的相干叠加，散斑的平均尺寸与散射介质对接收面的张角 $\alpha$ 有关。

$\delta_x\approx\frac{\lambda z}{L}=\frac{\lambda}{\alpha}$

$\delta_{z}\approx\lambda(\frac{z}{L})^{2}=\frac{\lambda}{\alpha^{2}}$

3.光学记忆效应

记忆效应：在一定视场范围内，散射介质由物面到像面的点扩散函数存在空域平移不变性。光学记忆效应范围受散射介质的厚度L的影响，与其他参数无关，因此我们可以用散斑相关函数（即散斑相关度）来描述记忆效应存在的范围：

$C(qL)=\left[\frac{qL}{\sinh(qL)}\right]^2$

其中， $q=2\pi\delta\theta/\lambda$ , $\delta\theta$ 为角度。由上式可得，在记忆效应的角度范围内，随转动角度的增大，散斑相关程度呈指数衰减。

$\Delta \theta <<\frac{\lambda}{\pi\cdot L}$

记忆效应（Memory Effect）是指在散射介质中，当入射光的入射角发生微小改变时，所观察到的散射光模式并不完全改变，而是保留了之前的信息，即存在相关性。这种相关性使得在散射介质中改变入射角度只会导致散射光场的旋转或整体的缩放，而不会导致完全不同的散射模式。

4.菲涅尔衍射

实际的衍射可以分为两种类型，在理想状态下，当光的传播距离为有限远时，一般采用菲涅耳衍射，反之，传播距离为无限远时，则采用夫琅和费衍射。?

平面波沿k方向传播时，在光场中坐标为（x,y,z）点处产生的复振幅可以表示为：

$U(x,y,z)=\alpha \cdot exp[jk(x\cos{\alpha}+y\cos{\beta}+z\cos{\gamma})]$

${\cos{\alpha}}^2+{\cos{\beta}}^2+{\cos{\gamma}}^2=1$

xy平面上复振幅分布可以表示为：?

$U(x,y)=A \cdot exp[jk(x\cos{\alpha}+y\cos{\beta})]$

假设一束单色光的波长为 $\lambda$ ，将衍射表面的光场分布设为 $U_0(x_0,y_0)$ ，光经过一段距离的传播到达接收面，接收面的光场分布为U(x,y)，如下式所示：

$U(x,y)=\frac{exp(jkd_1)}{j\lambda d_1}\iint U_0(x_0,y_0)exp\left \{ \frac{jk}{2d_1}[(\grave{x}-x_0)^2+(\grave{y}-y_0)^2] \right \}dx_0dy_0$

其中，光波数:? $k=\frac{2 \pi}{\lambda }$

$U(x,y)=\frac{exp(jkd)}{j\lambda } exp\left \{ \frac{jk}{2d} {(x^2+y^2)} \right \} \iint U_0(x_0,y_0)exp[\frac{jk}{2}(x_0^2+y_0^2)]\times exp[-j2\pi(x_0\frac{x}{\lambda d}+y_0\frac{y}{\lambda d})dx_0dy_0]$

化简可得：

$U(x,y)=\frac{exp(jkd)}{j\lambda d} exp\left \{ \frac{jk}{2d} {(x^2+y^2)} \right \} FFT\left \{ U_0(x_0,y_0)exp[\frac{jk}{2d}(x_0^2+y_0^2)] \right \}$

上式中，FFT为傅里叶变换

此方法采用单次傅里叶变换来求解菲涅尔衍射积分，称为单次快速傅里叶变换（Single Fast Fourier Transform, S-FFT）算法。

5.菲涅尔衍射-凸透镜成像

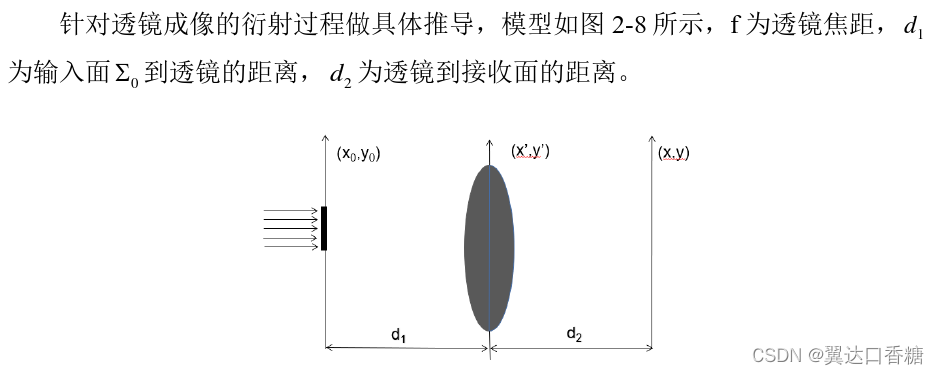
入射光从入射面经过衍射到透镜前表面，距离为有限远，采用菲涅尔衍射，透镜前表面的光场分布U1(x',y')?
$U(x,y)=\frac{exp(jkd)}{j\lambda d} exp\left \{ \frac{jk}{2d} {(x^2+y^2)} \right \} FFT\left \{ U_0(x_0,y_0)exp[\frac{jk}{2d}(x_0^2+y_0^2)] \right \}$
透镜对光场产生影响，光在透镜后表面的分布为?
$U'_1(x',y')=U_1(x',y')\exp\biggl(-jk\frac{\left(x'\right)^2+\left(y'\right)^2}{2f}\biggr)P(x',y')$
上式中将所使用透镜的孔径函数表示为P(x',y')，光穿过透镜，在经过一段距离
的衍射到达接收面时，光场分布情况如下：?

$U_{1}(x,y)=\frac{\exp(jkd_{2})}{j\lambda d_{2}}\iint U^{\prime}{}_{1}(x^{\prime},y^{\prime})\exp\left\{\frac{jk}{2d_{2}}\Big[\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}\Big]\right\}dx^{\prime}dy^{\prime}$

光从透镜后表面到接收面这一段距离也是有限远，故也采用菲涅尔衍射进行推导。?

6.光的传输过程

U1(平面波)???U2(衍射)? ?U3(传矩阵)?U4(衍)?U5(物)? ???U6(衍射)? ? ? U7(传输矩阵)? ???

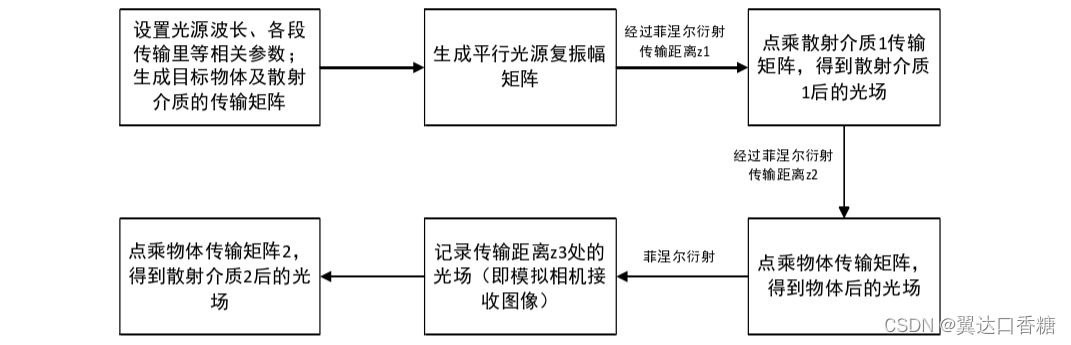
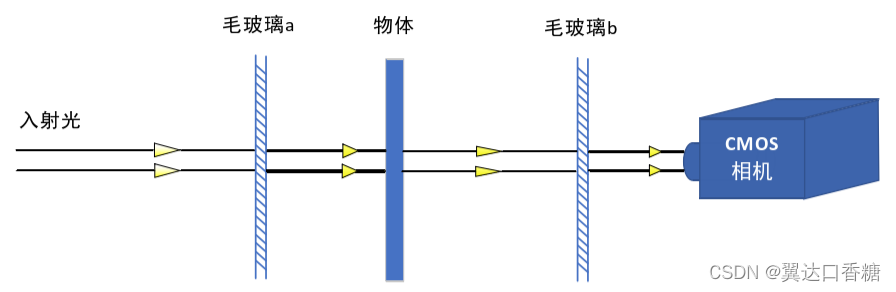
(1) 光源发出的光首先经过一个透镜进行准直，把准直后的光看作平面波，而不是高斯光束，记作𝑈1；?
(2) 根据惠更斯－菲涅尔原理，入射光经过一段菲涅尔衍射过程传播到第一层散射介质层（随机相位屏）前，得到照射散射介质层（随机相位屏）的复振幅分布，记为𝑈2；?
(3) 照射散射介质层的复振幅被散射介质层进行相位扰乱后得到𝑈3，再经过一段长度为𝑧1的菲涅尔衍射过程传播到物体前表面得到𝑈4。?
(4) 光波传输到物体前表面后，与物体O进行点乘得：??
$U_5=O \cdot U_4$
(5) 再经过一段长度为z2的菲涅尔衍射到达第二层散射介质前，记为U6。?
(6) 第二层散射介质模型同步骤（3），得到第二层散射介质后的光波U7。?

7.传输矩阵

前向传播的输入场和输出场的关系可以通过矩阵方程表示：

$u_{out}=Tu_{in}$

入射场Uin是一个1 × N的矩阵，出射场Uout是一个1 × M的矩阵。T是一个N × M的复数矩阵，用来表征由波动方程中的非均匀折射率引起的输入和目标平面之间的散射。T也叫做传输矩阵。?

传输矩阵模型表明给定一个任意的输入场，可以得到输出光场上的光的振幅和相位。对于输出场某一目标位置

$u_m^{out}=\sum_n^Nt_{mn}u_n^{in}=\sum_n^Nt_{mn}A_ne^{i\phi_n}=\sum_n^N(A_{mn}e^{i\phi_{mn}})(A_ne^{i\phi_n})$

其中， $t_{mn}=A_{mn}e^{i\phi_{mn}}$ 是传输矩阵中元素的表示。

8.波前整形调制

调制的目标是使得评估指标最大化，回到基本公式：

$u_m^{out}=\sum_n^Nt_{mn}u_n^{in}$

这个指标就是增强因子：

$\eta=\frac{I_{opt}}{I_{ref}}$

$I_{ref}$ 假设不变，输出光 $\beta$ 通道中的光强要最大：?

$I_{opt}=I_{\beta}=\mid u_{\beta}^{out}\mid^2={\left | \sum_n^N(A_{mn}e^{i\phi_{mn}})(A_ne^{i\phi_n}) \right |}^2$

$I_{opt}={\left | \sum_n^N(A_{mn}A_ne^{i(\phi_{mn}+\phi_n)}) \right |}^2$

当 $\phi_{n}=-\phi_{mn}$ 时，这个时候取得最大值。

理论上可以实现的最大增强是：

$\eta=\alpha(N-1)+1$

N为独立控制的输入通道数。

对于多目标优化来说，这个指标则需要更加丰富一些

$f_1=\sum_{\mathrm{n=1}}^NI_\mathrm{n}\left/I_{ref}\right.$

$f_2=\frac{\sigma_N}{\frac{1}{N}\sum_{\mathrm{n=1}}^NI_\mathrm{n}}\times100\%$

f1值越大表示聚焦点的总峰值背景比越高，f2越小表示多个聚焦点之间越均匀，聚焦效果越好。

9.光与物体的相互作用

传感器采集到的二维强度图像Ｉ可以表示为二维待观测目标物Ｏ与PSF的卷积：

$I=O*F_{PSF}$

$F_{PSF}$ 是指点扩散函数（Point Spread Function），它是用于描述光学系统中点光源成像的特性的函数。

介质内的点扩散函数：

将散射介质PSF由散斑形态校正为脉冲函数δ形态，进而直接在记忆效应范围内实现透过散射介质的成像：

$I=O*\delta =O$

10.反卷积成像

$I=O*F_{PSF}$

$O=Deconv(I,F_{PSF})$

11.自相关成像

由于PSF自相关为尖峰函数，其具有良好的峰值集中性和能量集中性。这意味着在进行PSF自相关恢复时，大部分的能量都集中在恢复图像的主要结构上，而不会引入额外的噪声或失真。这使得PSF自相关成为一种有效的图像恢复方法。

自相关的关系：

$F\left \{ I \otimes I \right \}=F\left \{ (O\otimes O)\star (F_{PSF} \otimes F_{PSF}) \right \}=F\left \{ (O\otimes O) \star \delta \right \}=F\left \{ O \otimes O \right \}={\left | F\left \{ O \right \} \right |}^2$

$I(x)=O(x)*F_{PSF}$

$F_{PSF,j} \otimes F_{PSF,k}=\begin{cases} 0& \text{j!= k}\\\delta& \text{j=k} \end{cases}$

根据Wiener–Khinchin定理，函数的自相关与其能谱密度构成傅里叶变换对：

$A(x,y)=I(x,y)\star I(x,y)=\mathcal{F}^{-1}\{|\mathcal{F}\{I(x,y)\}|^2\}$

为了使图像恢复更加高质高效，我们引入一个窗口函数来获得有效功率谱。窗口函数本质上为加权函数

$S(k_x,k_y)=|\mathcal{F}\{W(x,y)A(x,y)\}|$

12.相位恢复算法

利用自相关关系可以获取到的目标物幅值谱信号,但傅里叶幅值信息不足以支撑目标物体的恢复，还需要得到目标物体的相位信息。一般用的比较多的是ER或者HIO。

设置随机初始值 $g_{k}(x,y)$ ，

$G_{k}\left(k_{x},k_{y}\right)=\mathcal{F}\{g_{k}(x,y)\}$

$\theta_{k}\left(k_{x},k_{y}\right)=\arg\{G_{k}(x,y)\}$

$G^{\prime}{}_{k}(k_{x},k_{y})=\sqrt{S_{meas}(k_{x},k_{y})}e^{i\theta_{k}(k_{x},k_{y})}$

$g_{k}^{\prime}(x,y)=\mathcal{F}^{-1}\{G_{k}^{\prime}(k_{x},k_{y})\}$ ?

所施加的物理约束为：非负实数和真实性。

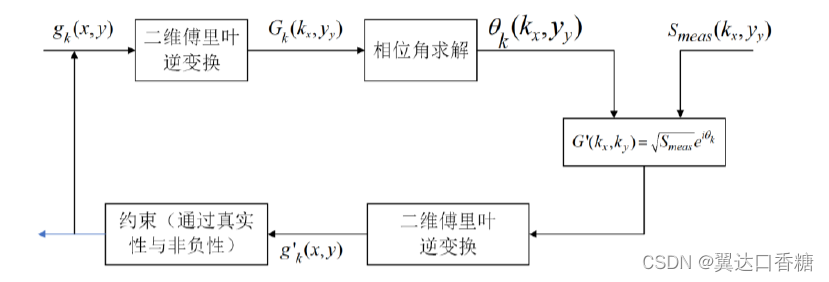
“错误减少（Error Reduction, ER）”

$\left.\mathfrak g_{k+1}(x,y)=\left\{\begin{matrix}g'_k(x,y)&\text{for}(x,y)\not\in\Gamma\\0&\text{for}(x,y)\in\Gamma\end{matrix}\right.\right\}$

ER算法在最初的迭代过程中呈现快速收敛的状态，但迭代速度随着迭代次数
的增加逐步降低，面对这种情况，提出了HIO算法：?

“混合输入输出(HIO Hybrid Input-Output,?HIO)”

$\left.g_{k+1}(x,y)=\left\{\begin{matrix}g'_k(x,y)&\text{for}(x,y)\not\in\Gamma\\g_k(x,y)-\beta g'_k(x,y)&\text{for}(x,y)\in\Gamma\end{matrix}\right.\right\}$
其中 $\Gamma$ 是 $g'_k(x,y)$ 上违反物理约束的所有点(x,y)的集合， $\beta$ 为衰减因子，起到控制算法收敛特性的作用。当估计对象满足恢复要求时，则停止迭代。

文章来源:https://blog.csdn.net/weixin_47567401/article/details/135308190
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！