肖恩会函数递归咯！

小伙伴们好久不见啊，肖恩拖更这么久，真是不好意思，嘿嘿，刚放假不久，来啦，那今天就先让我们看看函数递归~~

1.递归是神马

递归是学习C语言函数绕不开的?个话题，那什么是递归呢？
递归就是?种解决问题的方法，在C语言中，递归就是函数自己调用自己。
把?个大型复杂问题层层转化为?个与原问题相似，但规模较小的子问题来求解；直到子问题不能再被拆分，递归就结束了。所以递归的思考方式就是把大事化小的过程。
递归中的递就是递推的意思，归就是回归的意思。

#include <stdio.h>
int main()
{
	printf("Hello world！");
	main();//main函数中又调?了main函数
	return 0;
}

这就是一个非常简单的递归的例子，上面的递归只是为了演示递归的基本形式，不是为了解决问题，代码最终也会陷入死递归，导致栈溢出（Stack overflow）（后面会讲解）。
那接下来我们就具体举几个例子来细细体会递归

2.递归举例

（1）求阶乘

n的阶乘的递归公式如下：

先来看代码

#include <stdio.h>

int Fact(int n)
{
	if (n == 0)
		return 1;
	else
		return n * Fact(n - 1);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int x = Fact(n);
	printf("%d\n", x);
	return 0;
}

（这里不考虑n太大的情况，n太大存在溢出）
来看图解

相信聪明的你们肯定看懂了，那我们来看第二个例子

（2）求第n个斐波那契数

直接上代码

int Fib(int n)
{
	if (n <= 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}

#include <stdio.h>

int main()
{
	int n = 0;
	scanf("%d", &n);
	int x = Fib(n);
	printf("%d\n", x);
	return 0;
}

这个代码求斐波纳契数完全没有问题，但是呢，当你们把n的值调得稍微大一点点，就会发现这个运行速度好像没想象的那么快，那么是为什么呢？答案肖恩待会儿再为大家揭晓

（3）模拟pow函数（整数次）

那么首先pow函数是啥呢，说白了就是求N的K次方是多少，那我们也可以用递归来模拟这个函数，也不难，代码如下

int POW(int n,int k)
{
	if (k > 0)
		return n * POW(n, k-1);
	else
		return 1;
}
#include <stdio.h>

int main()
{
	int n = 0;
	int k = 0;
	printf("n,k:");
	scanf("%d%d", &n,&k);
	int x = POW(n,k);
	printf("%d", x);
	return 0;
}

这个和求阶乘那个还是很相似的，我们稍微上点难度

（4）模拟strlen函数

“strlen函数” 是一个C语言中的字符串函数，用来计算字符串的长度，即字符串中字符的个数。这个函数返回一个整数值，表示字符串的长度。
我们可以利用递归来模拟实现一下这个函数

#include <stdio.h>

int my_strlen(char* str)
{
	if (*str != '\0')
		return my_strlen(str + 1)+1;
	else
		return 0;
}
int main()
{
	char* str = "abc";
	int len = my_strlen(str);
	printf("%d",len);
	return 0;
}

（5）喝饮料

喝汽水，1瓶汽水1元，2个空瓶可以换一瓶汽水，给20元，可以喝多少汽水。
这个问题我们用普通的循环可以解决

#include <stdio.h>

int main() {
    int money = 20; // 初始金额
    int bottles = money; // 初始瓶数
    int total = money; // 初始总共可以喝的汽水数

    while (bottles >= 2) {
        int new_bottles = bottles / 2; // 用掉的瓶数换来的新瓶数
        total += new_bottles; // 新喝到的汽水数
        bottles = new_bottles + (bottles % 2); // 剩余的瓶数（加上不能换的瓶数）
    }

    printf("总共可以喝 %d 瓶汽水\n", total);

    return 0;
}

当然，递归也可以的哦

#include <stdio.h>

int drinkSoda(int money, int bottles) {
    if (bottles < 2) {
        return 0;
    }
    int new_bottles = bottles / 2;
    int new_sodas = new_bottles;
    int remaining_bottles = new_bottles + (bottles % 2);
    return new_sodas + drinkSoda(money, remaining_bottles);
}

int main() {
    int money = 20; // 初始金额
    int bottles = money; // 初始瓶数

    int total = money + drinkSoda(money, bottles);

    printf("总共可以喝 %d 瓶汽水\n", total);

    return 0;
}

不知道大家有没有看懂呢

（6）求一个数每位数的和

递归的限制条件

如：n=1234 sum=1+2+3+4

int Sum(int n) {
		return n % 10 + Sum(n / 10);
}
#include <stdio.h>

int main()
{
	int n = 0;
	printf("n:");
	scanf("%d", &n);
	int x = Sum(n);
	printf("%d", x);
	return 0;
}

哎，眨眼一看是不是没什么问题啊，当你运行时就会发现什么都没有（这就是我犯下的一个错误）

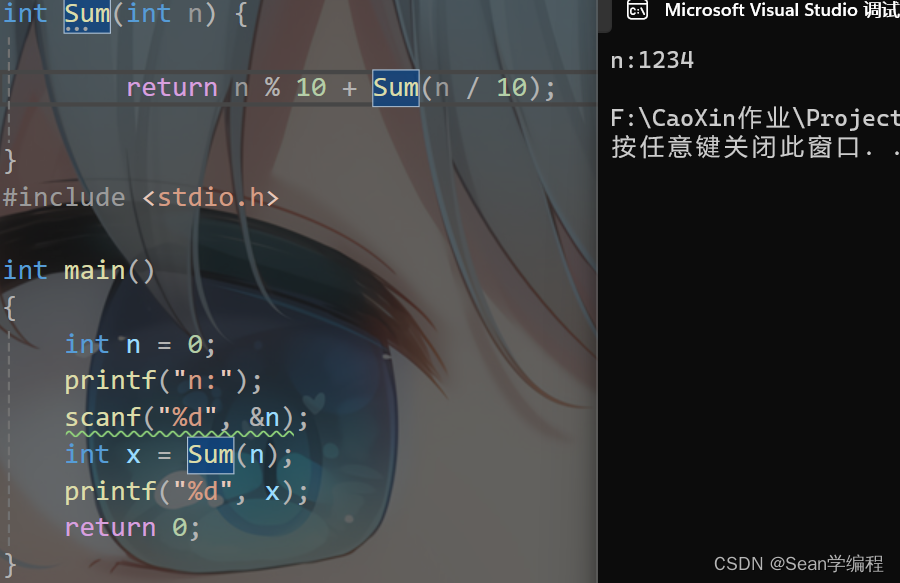
为什么呢，我们来调试看一下

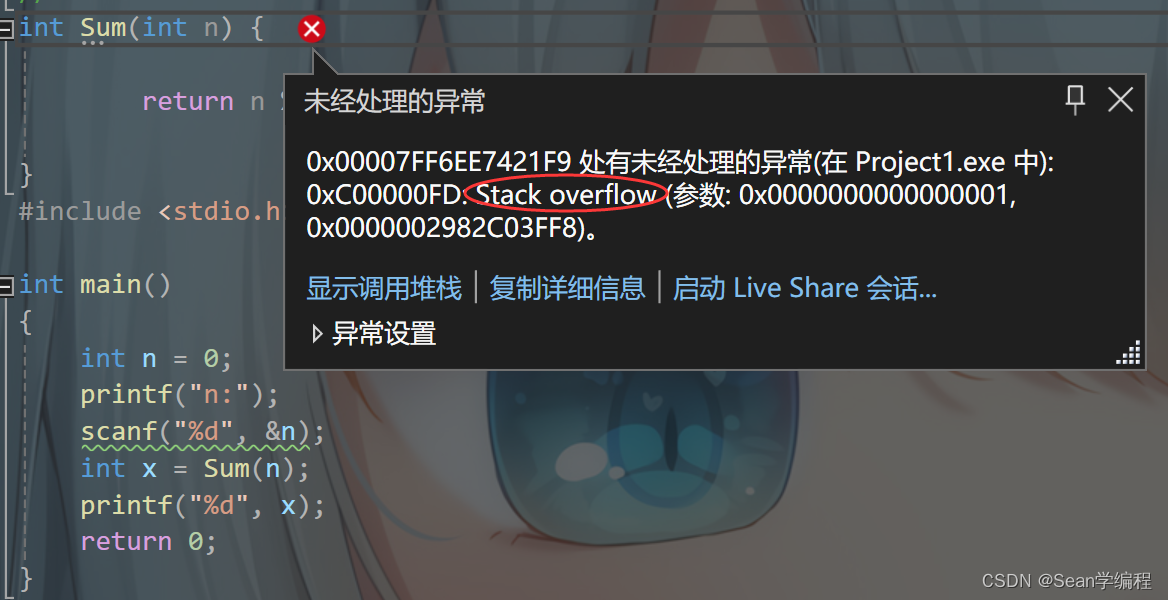
我们可以看到，栈溢出了，那么，为什么呢？因为我们没有添加限制条件，从而导致无限递归下去，然后就会导致栈溢出
递归在书写的时候，有2个必要条件：
? 递归存在限制条件，当满足这个限制条件的时候，递归便不再继续。
? 每次递归调用之后越来越接近这个限制条件。
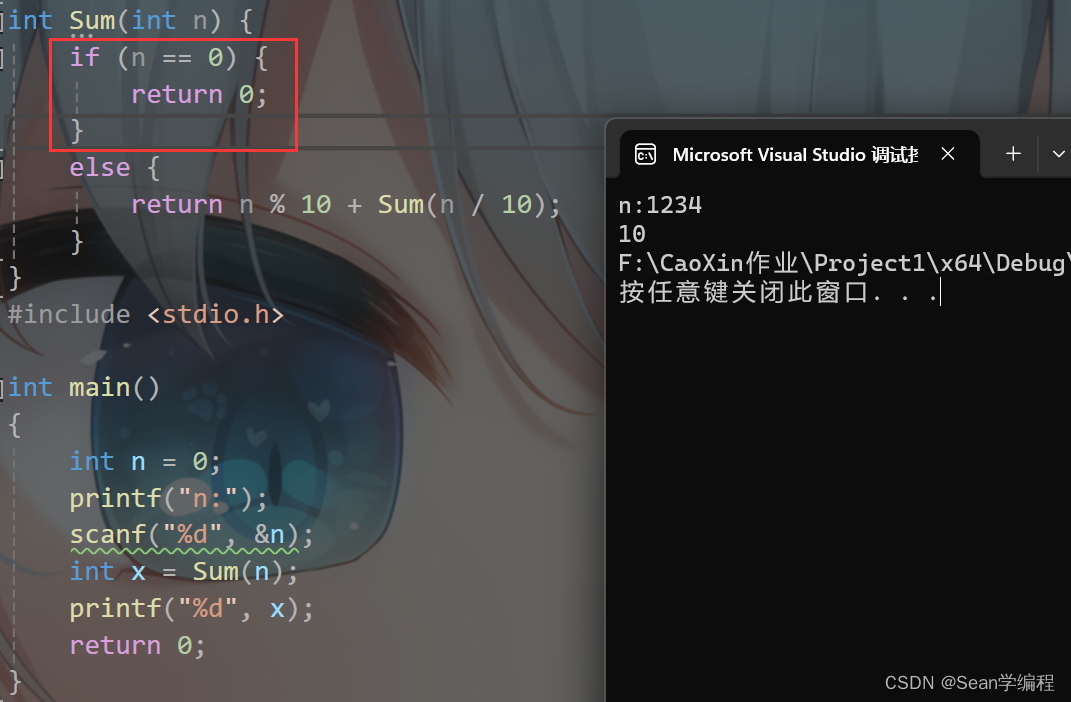
只需要稍加修改

int Sum(int n) {
	if (n == 0) {
		return 0;
	}
	else {
		return n % 10 + Sum(n / 10);
	}
}
#include <stdio.h>

int main()
{
	int n = 0;
	printf("n:");
	scanf("%d", &n);
	int x = Sum(n);
	printf("%d", x);
	return 0;
}

（7）汉诺塔

"汉诺塔"是一种经典的数学谜题和智力游戏，由法国数学家爱德华·卢卡斯发明。游戏包括三根柱子和一些不同大小的圆盘，最初都堆叠在一根柱子上。目标是将所有圆盘从一根柱子移动到另一根柱子，规则是一次只能移动一个圆盘，并且大圆盘不能放在小圆盘上面。这个游戏被用来展示递归算法和数学原理。
https://apps.fuyeor.com/zh-cn/games/hanoi/
上面这个网址可以去玩一下这个汉诺塔的小游戏体会体会

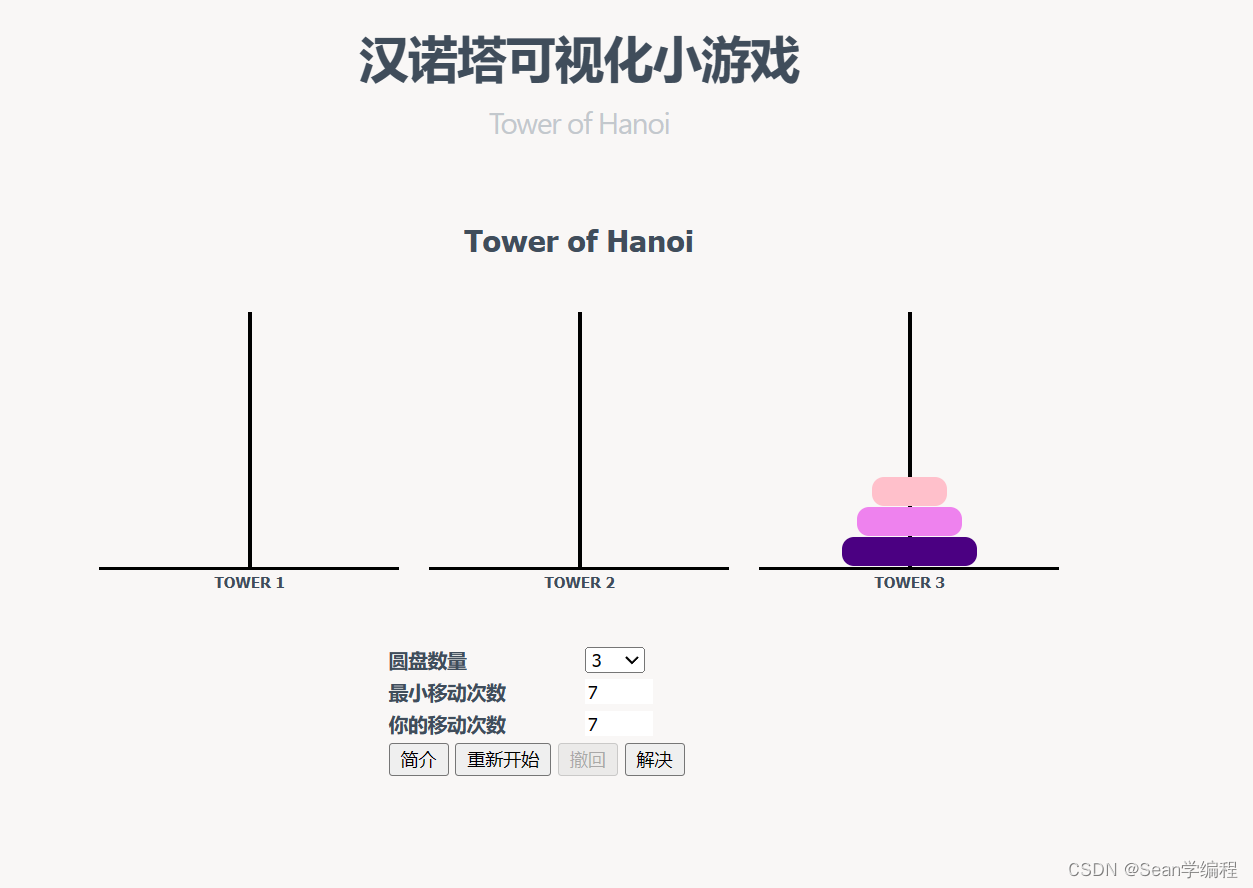
我在这里把这三个柱子分别命名为A柱B柱和C柱

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int count = 0;
void hanoi(int n, char a, char b, char c)
{
	if (n == 1)
	{
		printf("%c-->%c\n", a, c);
		count++;
	}
	else {
		hanoi(n - 1, a, c, b);
		printf("%c-->%c\n", a, c);
		count++;
		hanoi(n - 1, b, a, c);
	}
}
int main()
{
	int n;
	printf("请输入汉诺塔层数:");
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
	printf("需要移动%d次\n", count);
	return 0;
}

肖恩相信有了上面的这么多例子大家肯定对递归也有了一定的了解，那我们接下来看看迭代和递归又有什么关系

3.递归与迭代

递归是?种很好的编程技巧，但是很多技巧?样，也是可能被误用的，就像举例1?样，看到推导的公式，很容易就被写成递归的形式。
所以如果不想使?递归就得想其他的办法，通常就是迭代的方式（通常就是循环的方式）。
比如：计算n的阶乘，也是可以产?1~n的数字累计乘在?起的。

int Fact(int n)
{
	int i = 0;
	int x = 1;
	for(i=1; i<=n; i++)
	{
	ret *= i;
	}
	return x;
}

上述代码是能够完成任务，并且效率是比递归的方式更好的。
事实上，我们看到的许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更加清晰，但是这些问题的迭代实现往往比递归实现效率更高。
当?个问题非常复杂，难以使用迭代的方式实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开销。
在上面的第二个例子说道当n比较大的时候它的速度就会比较慢，当我们n输入为50的时候，需要很长时间才能算出结果，这个计算所花费的时间，是我们很难接受的，这也说明递归的写法是非常低效的，那是为什么呢？
其实递归程序会不断的展开，在展开的过程中，我们很容易就能发现，在递归的过程中会有重复计算，而且递归层次越深，冗余计算就会越多。我们可以做测试：

#include <stdio.h>
int count = 0;
int Fib(int n)
{
i	f(n == 3)
		count++;//统计第3个斐波那契数被计算的次数
	if(n<=2)
		return 1;
	else
		return Fib(n-1)+Fib(n-2);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d\n", ret);
	printf("\ncount = %d\n", count);
	return 0;
}

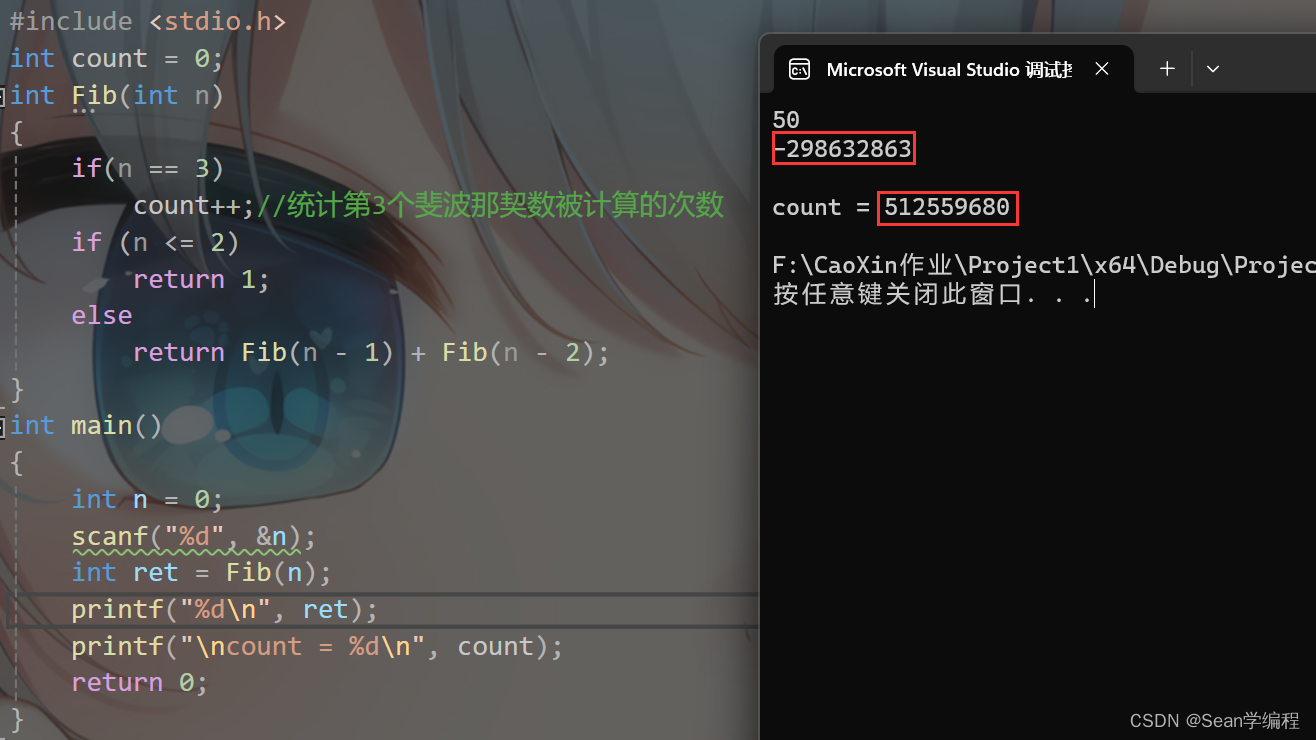
我们可以看到在计算的五十个斐波那契数的时候数据已经溢出了并且统计的三个斐波那契被计算的次数已是非常高这些计算是非常冗余的。所以斐波那契数的计算，使用递归是非常不明智的，我们就得想迭代的方式解决。
我们知道斐波那契数的前2个数都1，然后前2个数相加就是第3个数，那么我们从前往后，从小到大计算就行了。
这样就有下面的代码：

int Fib(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	while(n>2)
	{
		c = a+b;
		a = b;
		b = c;
		n--;
	}
	return c;
}

迭代的方式去实现这个代码，效率就要高出很多了。
有时候，递归虽好，但是也会引入?些问题，所以我们?定不要迷恋递归，适可而止就好。
那么以上呢就是递归的全部内容。
那么在最后呢，肖恩依旧给大家附上一张照片

感谢大家的阅读，咱们下期再见~~~