1058：求一元二次方程 ------ 信息学奥赛高级题库

【题目描述】

利用公式x1= (-b + √(b2-4ac)) / 2a，x2= (-b - √(b2-4ac)) / 2a，求一元二次方程ax2+bx+c=0的根，其中a不等于0。结果要求精确到小数点后5位。

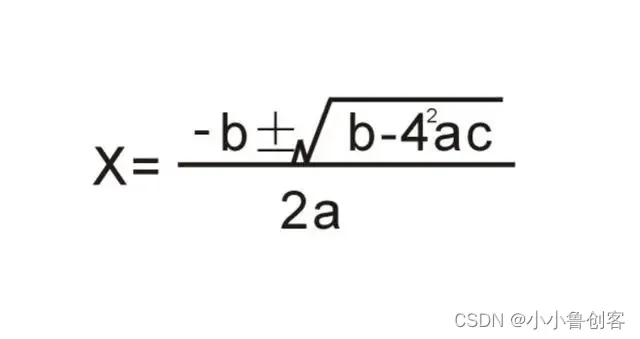
【输入】

输入一行，包含三个浮点数a,b,c（它们之间以一个空格分开），分别表示方程ax2+bx+c=0的系数。

【输出】

输出一行，表示方程的解。

若两个实根相等，则输出形式为：“x1=x2=”；

若两个实根不等，在满足根小者在前的原则，则输出形式为：“x1=...;x2=...“；

若无实根输出“No answer!”。

所有输出部分要求精确到小数点后5位，数字、符号之间没有空格。

【输入样例】

-15.97 19.69 12.02

【输出样例】

x1=-0.44781;x2=1.68075

【知识点】

一元二次方程

通过化简后，只含有一个未知数（一元），并且未知数的最高次数是2（二次）