曼哈顿距离+蛇形走位

题目：

1219. 移动距离 - AcWing题库

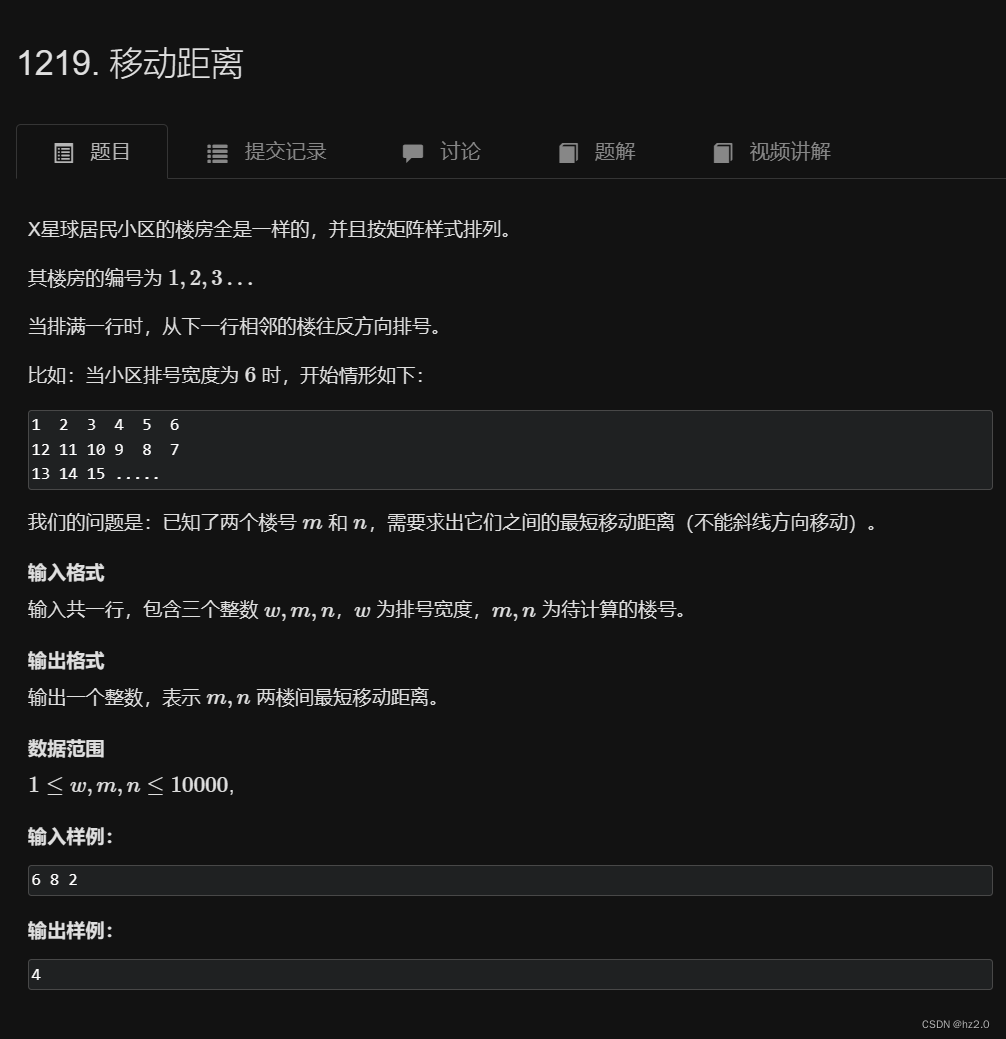
思路：?

1.曼哈顿距离->两点矩阵坐标行列差值的绝对值?->二维数组。

2.1，2，3，4~的连续数字，为与数组下标对应->将所以数字全部减一，从0开始。

3.二维数组行下标：i=(x-1)/w。

4.蛇形走位的二维数组列下标：若行下标为偶，则列下标：j=(x-1)%w；若行下标为奇，则列下标：j=w-1-j。

若不蛇形走位：

若蛇形走位：

?

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;

int main()
{
    int w,m,n;
    cin>>w>>m>>n;
    int i1,i2,j1,j2;
    i1=(m-1)/w;
    i2=(n-1)/w;
    j1=(m-1)%w;
    j2=(n-1)%w;
    if(i1%2==1)j1=w-1-j1;
    if(i2%2==1)j2=w-1-j2;
    cout<<abs(i1-i2)+abs(j1-j2);
    
}

?