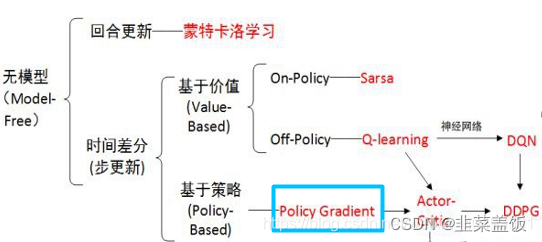
强化学习------Policy Gradient算法公式推导

一、前言

Policy Gradient 算法是一种基于策略的强化学习算法，与基于值的方法（如Q-learning和DQN）不同。基于值的方法主要关注于学习值函数（如状态值函数或者动作值函数），然后通过值函数来选择最优的动作。而Policy Gradient 算法则直接优化策略函数，通过梯度上升来最大化长期累积奖励。
简单来说
基于策略的算法给出了智能体在特定状态下应该采取的动作的概率分布
基于值的算法是给出智能体在特定状态下每一个动作的Q值

策略梯度（Policy Gradient）是基于策略搜索方法中最基础的方法，要理解AC，DDPG需要先学习策略梯度。学习策略梯度（Policy Gradient），要明白其原理，更是离不开其公式的推导。

二、公式推导

主要思想是使最终的回报最大，即一个完成的交互episode（从初始状态到最终状态的一个策略τ
）。
目标：一条完整的episode的回报期望最大

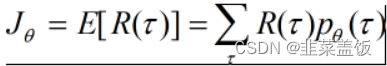
要使该目标最大，则参数θ的更新方向为梯度上升的方向。

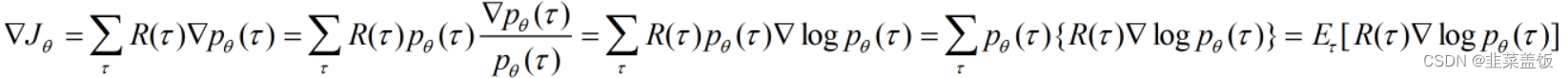
此公式中有两点需要注意：

• 第三个等号后的常用变换为：?f(x)=f(x)?logf(x)
• 最后一步一p(τ)是概率，与累加和可以看成是求后面部分的期望

下面我们来推导?logP(τ∣θ)

策略τ产生的轨迹如下：τ = {s1,a1,r1,s2,a2,r2,?,sT,aT,rT}
则该轨迹的概率可以用联合概率来表示：

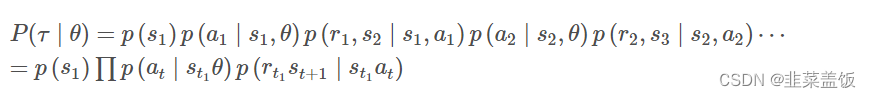
注意上式中只有$p(a_t|s_t,\theta )$与θ有关，其他均无关，因此对其去对数并求导可以转化为：

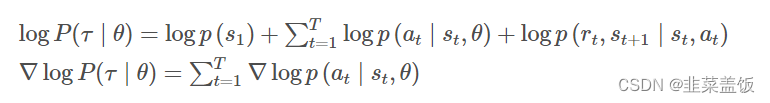
注意：我们对θ求导，不带θ的项，求导之后为0

这样我们就求出了?logP(τ∣θ)，带回到刚才的$?J_{\theta }$中，得到：

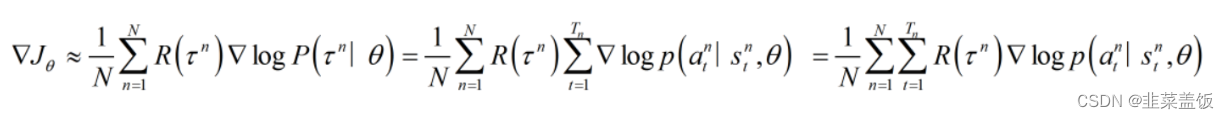
注意：期望就是均值，所以下面两个公式可以当作等价

与

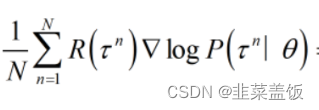
近似相等，可以理解为等价。

到此为止我们找到了误差的梯度$?J_{\theta }$，由此来构建神经网络的误差。

基线

在对动作进行采样时，无法保证每个动作都能抽取到，如果R都是正值，则每个动作的概率都会增大，对每抽取到的动作不公平，将上式减去一个值，保证其均值不变，梯度如下所示：

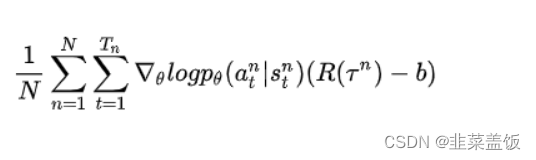
三、代码实现

代码示例放在另外一篇博客里面了，需要的可以跳转查看

代码

四、参考

Policy Gradient算法