基于车辆运动学的规划算法 - Hybrid A*/ State Lattice Planning (前置知识:自行车模型、Dubins、Reeds Shepp、多项式曲线、螺旋曲线)
本文将按顺序讲解自行车模型、Dubins和Reeds Shepp曲线、多项式曲线、螺旋曲线,再讲解两个案例:混合A*和State Lattice Planning
1 自行车模型

自行车模型:简化左右轮为一个轮子
两个自由度:后轮提供纵向速度或者加速度信息,前轮提供转向信息
自行车模型有三种定义参考点的方式:后轴中心、质心、前轴中心

基本假设:
(1)车辆在一个二维平面上运动(不会考虑上下坡和颠簸路段的运动)
(2)不考虑轮胎的滑移:假定车轮的运动方向和速度方向相等的
高速轮胎会有变形,轮胎的实际速度方向可能和当前车轮方向不一致。
1.1 以后轮为参考点的单车模型

世界坐标系后轴中心的坐标:
(
x
,
y
,
θ
)
(x,y,\theta)
(x,y,θ)
系统的输入:
v
、
ξ
v、\xi
v、ξ

有了上面的运动学模型,给定一个初始量
(
x
0
,
y
0
,
θ
0
)
(x_0,y_0,\theta_0)
(x0?,y0?,θ0?),系统的初始输入
(
v
0
、
ξ
0
)
(v_0、\xi_0)
(v0?、ξ0?),同时给定一小段时间
Δ
t
\Delta t
Δt,通过这个模型,就能预测下一时刻的状态
(
x
1
,
y
1
,
θ
1
)
(x_1,y_1,\theta_1)
(x1?,y1?,θ1?)
1.2 以前轮为参考点的单车模型


给定一个初始量
(
x
0
,
y
0
,
θ
0
)
(x_0,y_0,\theta_0)
(x0?,y0?,θ0?),系统的初始输入
(
v
0
、
ξ
0
)
(v_0、\xi_0)
(v0?、ξ0?),同时给定一小段时间
Δ
t
\Delta t
Δt,通过这个模型,就能预测下一时刻的状态
(
x
1
,
y
1
,
θ
1
)
(x_1,y_1,\theta_1)
(x1?,y1?,θ1?)
1.3 以质心为参考点的单车模型


1.4 前向积分

(1)使用转向角作为输入会导致转向角瞬间变化,所以更准确的是使用转向角的变化率
?
\phi
?作为模型的输入
(2)离散化模型,给定输入
[
v
,
?
]
[v,\phi]
[v,?]生成下一个状态
2 运动基元的生成方法
2.1 Dubins曲线
Dubins曲线

Task:最小化曲线的长度(汽车在任意起点
q
I
q_I
qI?和终点
q
G
q_G
qG?行驶)

假定速度为常量,系统被简化为:

u u u选自区间 U = [ ? t a n ? m a x , t a n ? m a x ] U=[-tan\phi_{max},tan\phi_{max}] U=[?tan?max?,tan?max?],进一步简化,假定 t a n ? = 1 tan\phi=1 tan?=1,满足 ? ∈ ( 0 , π / 2 ) \phi\in (0,\pi /2) ?∈(0,π/2)
Dubins证明了对于两个配置(位姿),Dubins曲线的最短路径总是表示不超过下面这三个运动基元的组合

(1) S:直行
(2) L:以最大转角向左运动
(3) R:以最大转角向右运动
Dubins曲线表明只有这六个词可能是最优的,任意两个配置之间的最短路径总是可以用这些词之一来表示:
L R L , R L R , L S L , L S R , R S L , R S R LRL,RLR,LSL,LSR,RSL,RSR LRL,RLR,LSL,LSR,RSL,RSR

L
/
R
L/R
L/R:下标表示在原有运动基元累积的旋转总量
S
S
S:下标表示行进的总距离
β
\beta
β:必须大于
π
\pi
π(如果小于
π
\pi
π,一定会有另一种组合是最优的)
对于给定的 q I q_I qI?和 q G q_G qG?,有两个问题
(1)哪一种组合最优:解析法求解
(2) α , β , γ , d \alpha, \beta ,\gamma, d α,β,γ,d的值如何表示 :几何法求解
2.2 Reeds Shepp曲线
Dubins曲线只允许车辆正向运动,Reeds Shepp曲线允许车辆反向运动

u
1
u_1
u1?:指定车辆前向或者后向
u 1 ∈ [ ? 1 , 1 ] u_1\in[-1,1] u1?∈[?1,1]
u 2 u_2 u2?:指定车辆向左还是向右、直行
u 2 ∈ [ ? t a n ? m a x , t a n ? m a x ] u_2\in[-tan\phi_{max},tan\phi_{max}] u2?∈[?tan?max?,tan?max?],进一步简化 u 2 ∈ [ ? 1 , 1 ] u_2\in[-1,1] u2?∈[?1,1],满足 ? ∈ ( 0 , π / 2 ) \phi\in (0,\pi /2) ?∈(0,π/2)
因为Reeds Shepp曲线引入了倒车,组合数也更多,有48种方式

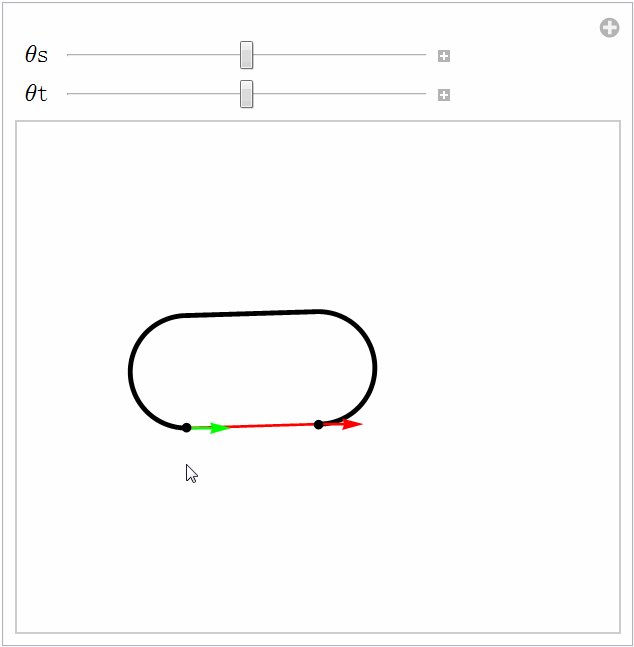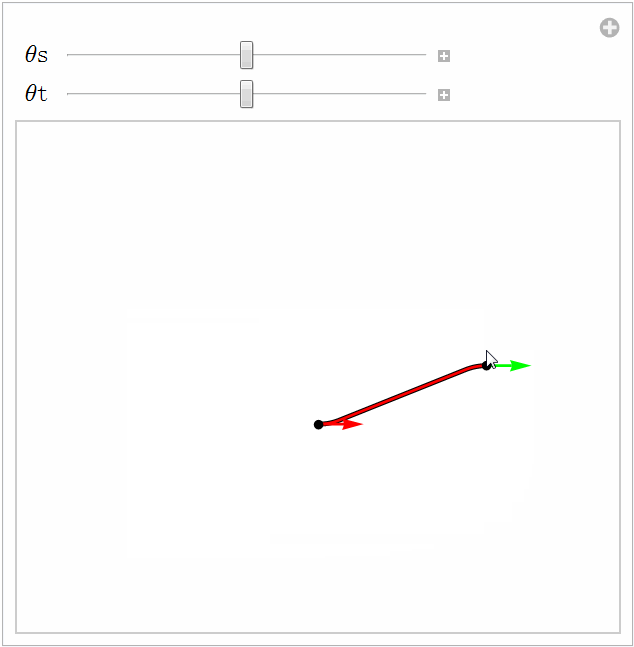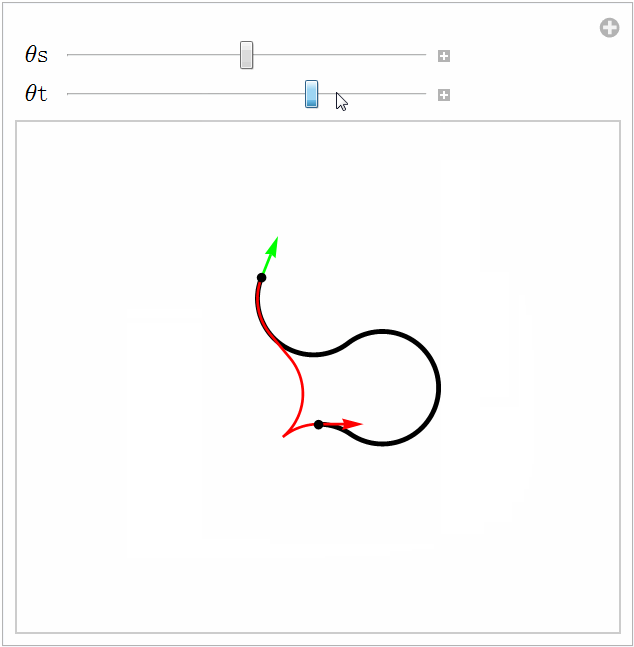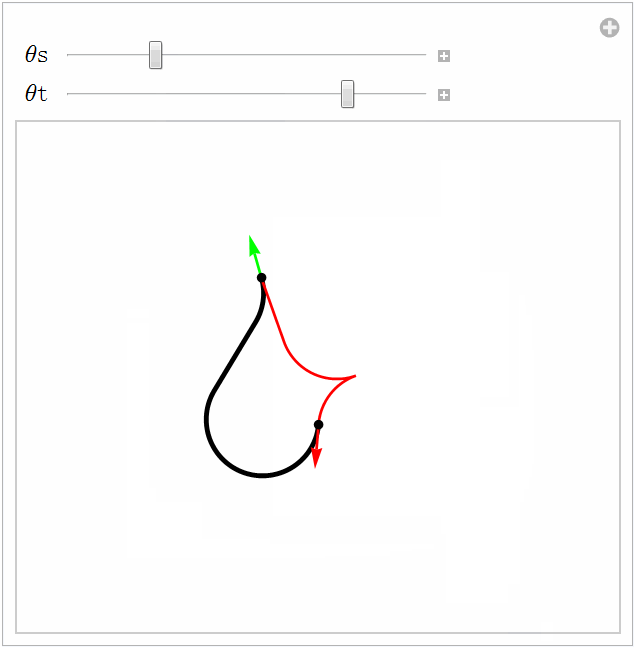
箭头表示汽车的朝向,红色曲线是Reeds-Shepp曲线,而黑色曲线是Dubins曲线。注意二者有时是重合的
只要存在连接起止位姿的无碰撞路径,就存在无碰撞的Reeds-Shepp曲线。但这个结果对Dubins曲线却不适用。
理论上存在但是没有给实际寻找的方法,采用随即搜索的方法,黑色表示障碍物
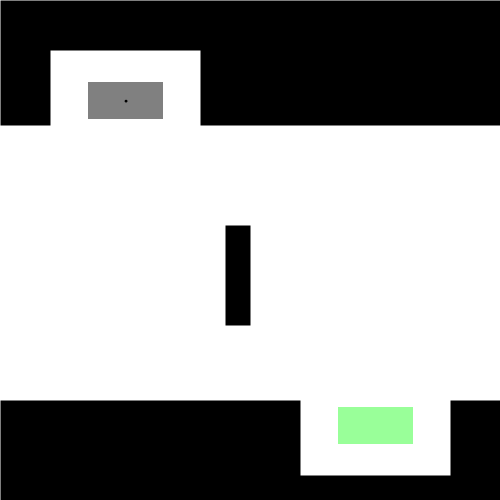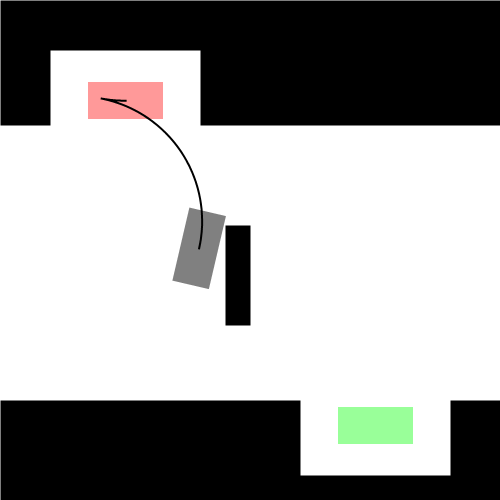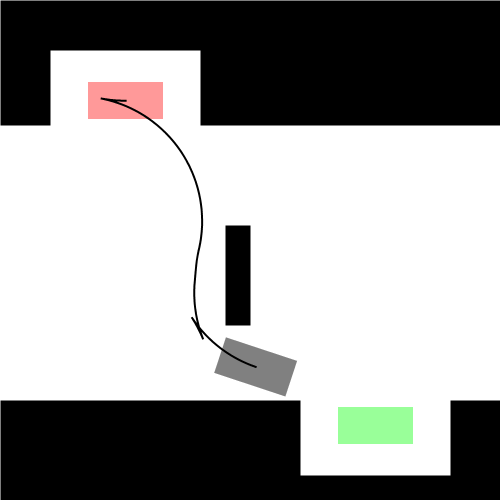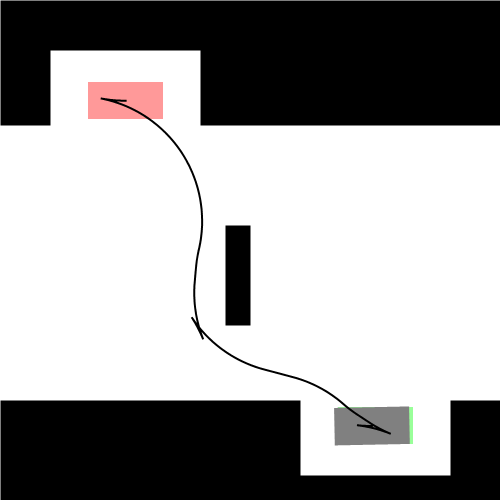
Dubins曲线和Reeds-Shepp曲线的用处
具有车轮的东西都属于非完整约束系统,不包括特殊的车轮(比如麦克纳姆轮),一般用Dubins曲线和Reeds-Shepp曲线作为复杂模型的近似最短路径,在实际执行时并不一定严格地遵循这些曲线
2.3 多项式曲线 - 五次多项式

五次多项式

开始点和终点状态作为边界条件
(
x
s
,
v
s
,
a
s
)
(x_s,v_s,a_s)
(xs?,vs?,as?)
(
x
e
,
v
e
,
a
e
)
(x_e,v_e,a_e)
(xe?,ve?,ae?)
具体推导详见:b站老王 自动驾驶决策规划学习记录(二)

五次多项式的应用
(1)在Frenet坐标系下,用五次多项式描述纵向
s
(
t
)
s(t)
s(t)和横向运动
l
(
t
)
l(t)
l(t)

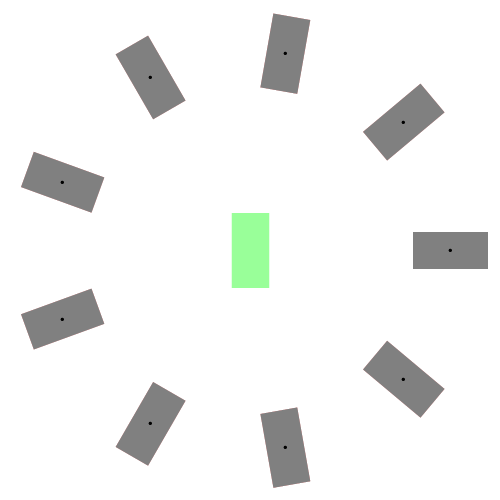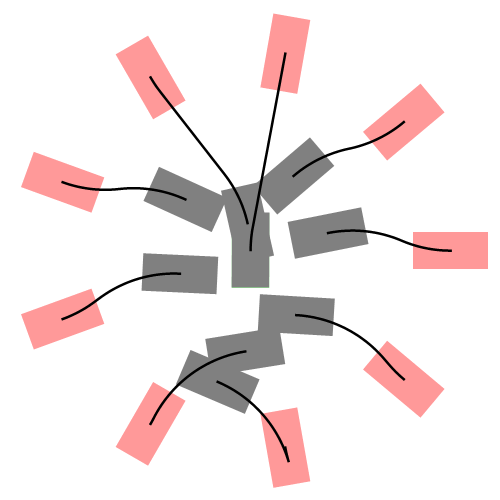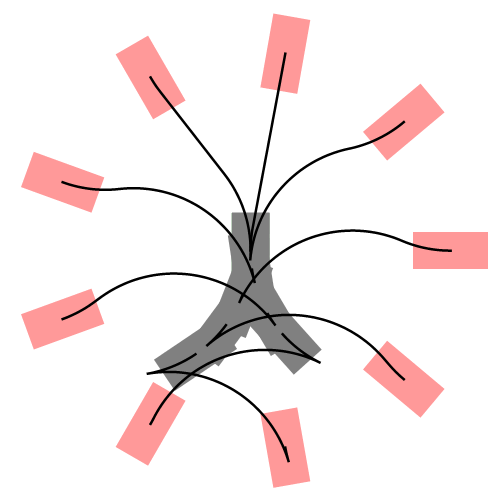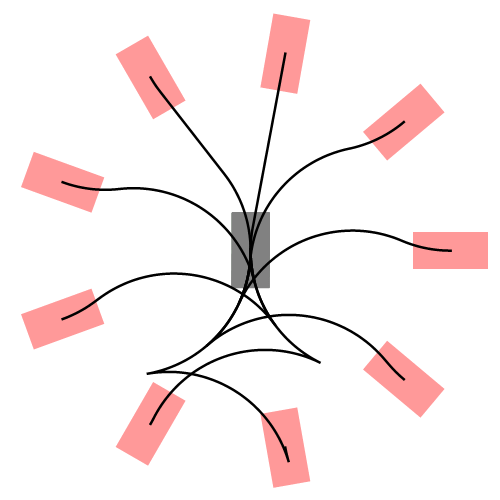
把横向和纵向运动结合得到如下在世界坐标系下的轨迹,然后选择一条最优(绿色)的轨迹

轨迹生成的完整流程

p
o
s
→
v
e
l
→
a
c
c
→
j
e
r
k
pos\to vel\to acc\to jerk
pos→vel→acc→jerk
五次多项式总体目标:
m
i
n
i
m
i
z
e
∫
0
T
j
e
r
k
2
(
t
)
d
t
minimize\int_{0}^{T} jerk^2(t)dt
minimize∫0T?jerk2(t)dt
(2)描述运动的方式
l
(
s
)
l(s)
l(s),
s
(
t
)
s(t)
s(t)

求解过程

(3)使用五次多项式生成状态格路径集

2.4 螺旋曲线 - Cubic Spiral Curve

螺旋曲线由曲率定义为弧长的函数
k
(
s
)
=
d
s
3
+
c
s
2
+
b
s
+
a
k(s)=ds^3+cs^2+bs+a
k(s)=ds3+cs2+bs+a
使用简单的运动学质点模型
k
=
d
θ
/
d
s
k=d\theta/ds
k=dθ/ds

螺旋位置没有闭式解。
x
(
s
)
,
y
(
s
)
x(s), y(s)
x(s),y(s) 的公式是
F
r
e
s
n
e
l
Fresnel
Fresnel积分

三角函数里面套了个函数,这种函数大多数没有解析解。
采用数值方法评估 F r e s n e l Fresnel Fresnel积分
S
i
m
p
s
o
n
Simpson
Simpson方法:

基本思想:
通过一个二次函数近似原函数的值


(1)Simpson的方法比其他更简单的数值方法(例如中点和梯形规则)更精确
(2)划分区间n决定了积分评估的准确性和效率
随着n增加,得到了更准确的近似,也会有更多的计算负担

求解a,b,c,d四个参数
工程技巧:对原问题做参数映射
(1) p 0 p_0 p0?和 p 3 p_3 p3?对应于给定的初始状态和结束状态,降低维度
(2)重映射公式 p 0 + p 1 s + p 2 s 2 + p 3 s 3 p_0+p_1s+p_2s^2+p_3s^3 p0?+p1?s+p2?s2+p3?s3确保 p i p_i pi?大小接近,在优化中添加数值稳定性

p
0
,
p
1
,
p
2
,
p
3
p_0,p_1,p_2,p_3
p0?,p1?,p2?,p3?对应沿整个路径等距的4个点处的曲率
s
f
s_f
sf?对应路径的总弧长

生成的多项式:

使用shooting方法求解参数

优化目标:

使用牛顿法做方程组求解


牛顿法基本思想:
(1)首先给定初值,然后用初值切线近似原函数的值
(2)迭代公式为
x
n
+
1
=
x
n
?
f
(
x
n
)
f
′
(
x
n
)
x_{n+1}=x_n-\frac{f(x_n)}{{f}^{'}(x_n)}
xn+1?=xn??f′(xn?)f(xn?)?
初值选择策略:
(1)从预先计算的查找表中获取
(2)采用上一次迭代的结果值作为当前的初值
3 Hybrid A*

基本思想:
(1)在控制空间采样,通过前向积分方式生成运动基元作为整个graph的边。
(2)使用栅格地图修建一些节点减少图的大小(如果多个state在一个栅格里,选择一个最优的state)
(3)使用类似A*的方法从状态图中搜索路径
搜索算法的图形比较

(1)A* 将成本与单元格的中心相关联,并且只访问对应于网格单元格中心的状态
(2)混合A* 将连续状态与每个单元格相关联,单元格的分数是其相关连续状态的成本
3.1 Hybrid A* 算法流程

算法流程基本与A*相似
有几处不同:
(1)g(n)累计成本:距离、改变行驶方向、惩罚转向等
(2)估计成本h(n):欧几里得/曼哈顿距离
(3)通过从控制空间和前向积分采样来展开邻居节点
(4)合并在离散空间中占据相同单元格的连续坐标状态
3.2 启发式函数设计
(1)Non-holonomic-without-obstacles
- 启发式函数考虑了车辆运动学的特征,最大转角,忽略了环境
- 估计基于Reeds Shepp路径的最短距离
(2)holonomic-with-obstacles
- 启发式函数没有考虑车辆运动学的特征,只考虑了障碍物
- 估计基于目标节点与当前正在扩展的顶点之间的最短距离

(a)欧几里得距离
(b)Non-holonomic-without-obstacles
(c)Non-holonomic-without-obstacles
(d)联合the non-holonomic-without-obstacles 和holonomic-with-obstacles
3.3 工程上面的trick
分析扩展

问题:离散化搜索永远不会达到精确的连续目标状态(精度取决于A*网格的分辨率)
解决:使用Reeds Shepp路径分析连接当前节点和目标
好处:这种方法大大提高了稀疏障碍物的搜索速度
分层规划

(1)Hybrid A* 生成的路径通常是次优的,值得进一步改进
(2)用共轭梯度(CG)下降法平滑混合A*路径
4 State Lattice Planning

基本思想:
(1)在状态空间下采样到一系列终点状态
Frenet坐标系(
l
,
l
′
,
l
′
′
l,l',l''
l,l′,l′′)、笛卡尔坐标系(
x
,
y
,
θ
,
k
x,y,\theta,k
x,y,θ,k)
(2)求解边界值BVP问题获得运动基元
(3)为每条path打分
(4)选择最优的path
4.1 Conformal Lattice

(1)在结构化道路行驶,Conformal Lattice定义了一种采样规则
(2)目标状态沿着道路从目标点横向偏移采样
(3)可以在避开障碍物的同时加快规划过程
4.2 规划过程
Sample Goal States
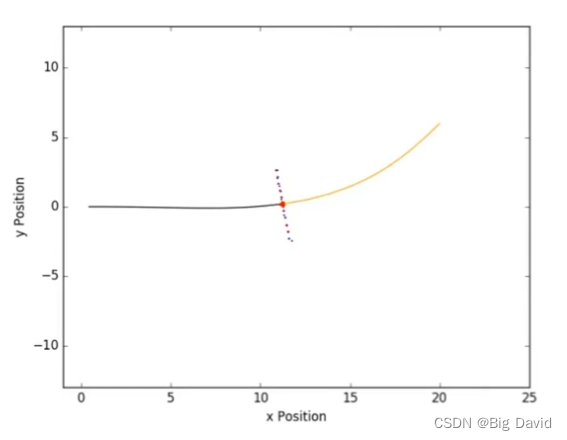
(1)目标状态沿道路从目标点横向偏移采样
(2)采样规则根据自车速度和其他因素调整
生成路径集合

解决BVP问题
(1)Frenet坐标系:五次多项式连接
(2)笛卡尔坐标系:三次螺旋曲线连接
打分和选择

成本函数设计:
(1)安全性

(2)平滑性

(3)中心偏移


5 正向运动学和逆向运动学方法的比较

正向运动学(控制空间采样)
(1)容易计算:给定初始状态和控制变量,通过整合运动学/动力学模型可以获得整个状态轨迹
(2)弱目标引导:依靠启发式函数来指导搜索过程
(3)具有更强的探索环境的能力
逆向运动学(状态空间采样)
(1) 难以计算:需要解决相对复杂的边界值问题
(2)强目标引导:直接向目标生成采样状态
(3)精心设计采样规则
非结构化场景(泊车)倾向于正向运动学方法,基于Hybrid思想,先搜一条粗解,再平滑实现泊车轨迹
结构化场景倾向于逆向运动学方法
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Mysql——索引相关的数据结构
- 数字信号处理实验---LSI系统的分析 Matlab代码
- 第 10 章 树结构的基础部分
- gitlab上传代码到仓库
- mysql学习打卡day15
- 使用Android Studio等idea工具开发flutter应用,必备的debug调试技能,非常好用
- vue 父传子 props
- 【浏览器】-- Chorme 常用命令行
- 绝缘电阻测试仪档位的选择技巧有哪些?这么一看就明白了!
- 海昌海洋公园用泛微千里聆RPA智能采集、识别、分析网络数据,助力优化运营服务