在做题中学习：三数之和

15. 三数之和 - 力扣（LeetCode）15. 三数之和 - 力扣（LeetCode）

解释：不能重复也就是说不能和前一个三元组的元素完全相同

思路：通过做 两数之和那道题 可以想到：

1.先排序

2.双指针法

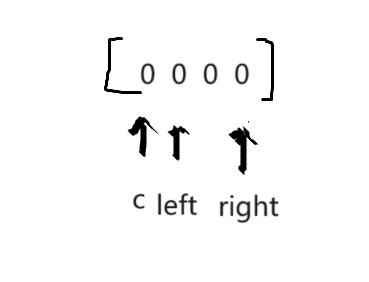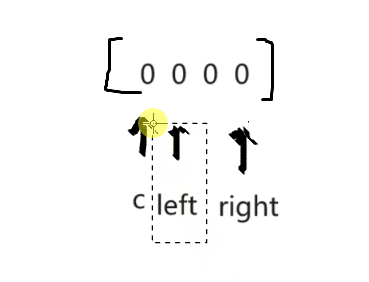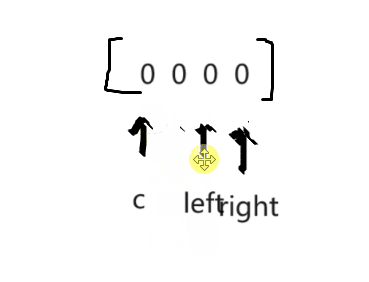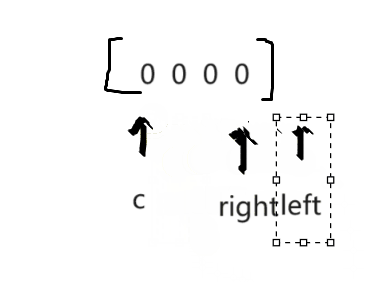
3.固定一个数c，另两个数相加 = -c? 就相当于找到了和为0的一组数。

细节：

1.去重

1.left的下一个 / right的前一个 如果和之前一样就需要跳过

2.c的下一个 和之前一样 也需要跳过

2.存三元组

用vector<vector<int>>存储，每一个三元组相当于一个一维数组。

3.优化

因为是用另两个数相加 = -c ，而因为定的c是排完序后的第一个负数，所以当c>0时，往后的结果也就不用看了。

4.注意

去重时小心越界，因为 极端情况可能会移出去，所以在去重时，也需要加上left<right

class Solution 
{
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        vector<vector<int>> v;
        //1.排序
        sort(nums.begin(),nums.end());
        int n = nums.size();
        for(int i = 0;i < n;)
        {
            //小优化
            if(nums[i] > 0)
            {
                break;
            }
            int left = i+1, right = n-1;
            while(left<right)
            {
                int sum = nums[left] + nums[right], target = -nums[i];

                if(sum < target)
                {
                    left++;
                }
                else if(sum > target)
                {
                    right--;
                }

                else
                {
                    v.push_back({nums[left],nums[right],nums[i]});
                    left++;
                    right--;
                    //去重
                    while(left < right && nums[left]==nums[left-1])
                    {
                        left++;
                    }
                    while(left < right && nums[right]==nums[right+1])
                    {
                        right--;
                    }
                }

            }
            //因为i去重会影响到for里的i，因此把i++设置在这里。
            i++;
            while(i < n && nums[i]==nums[i-1])
            {
                i++;
            }
        
        }
        return v;
    }
};