LeetCode刷题--- 目标和
发布时间:2023年12月23日
个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
个人专栏
力扣递归算法题
【C++】? ? ? ? ?
数据结构与算法
前言:这个专栏主要讲述递归递归、搜索与回溯算法,所以下面题目主要也是这些算法做的 ?
我讲述题目会把讲解部分分为3个部分:
1、题目解析
2、算法原理思路讲解
3、代码实现
目标和
题目链接:目标和
题目
给你一个非负整数数组?nums?和一个整数?target?。
向数组中的每个整数前添加?'+'?或?'-'?,然后串联起所有整数,可以构造一个?表达式?:
- 例如,
nums = [2, 1]?,可以在?2?之前添加?'+'?,在?1?之前添加?'-'?,然后串联起来得到表达式?"+2-1"?。
返回可以通过上述方法构造的、运算结果等于?target?的不同?表达式?的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
解法
题目解析
- 题目的意思非常简单,给我们一个非负整数数组?
nums?和一个整数?target?。 - 向数组中的每个整数前添加?
'+'?或?'-'?,然后串联起所有整数,可以构造一个?表达式?。 - 表达式的值要等于 target 有多少个。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
算法原理思路讲解?
对于每个数,可以选择加上或减去它,依次枚举每?个数字,在每个数都被选择时检查得到的和是否等于?标值。如果等于,则记录结果。
一、画出决策树
以 nums[ ] = [1,2,3] 和 target = 2 为例子
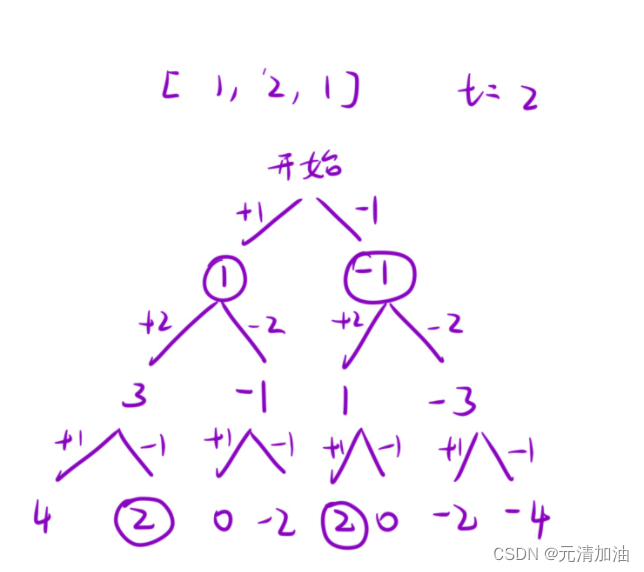
决策树就是我们后面设计函数的思路
二、设计代码
(1)全局变量
int sum;
int ret;- sum(target的值)?
- ret(记录符合target 值的次数)
(2)设计递归函数
void dfs(vector<int>& nums, int pos, int path);- 参数:nums(数组),pos(当前要处理的元素下标),path(当前状态和);
- 返回值:无;
- 函数作?:查找所有值为 target 的次数;
递归流程:
- 递归结束条件:pos?与数组?度相等,判断当前状态的 path?是否与?标值(target)相等,若是计数(ret)加?;
- 选择当前元素进?加操作,递归下?个位置,并更新参数 path;
- 选择当前元素进?减操作,递归下?个位置,并更新参数 path;
以上思路讲解完毕,大家可以自己做一下了
代码实现
时间复杂度:O(),其中 n?是数组 nums 的长度。回溯需要遍历所有不同的表达式,共有
?种不同的表达式,每种表达式计算结果需要 O(1) 的时间,因此总时间复杂度是 O(
)。
空间复杂度:O(n),其中 n?是数组 nums 的长度。空间复杂度主要取决于递归调用的栈空间,栈的深度不超过 n。
class Solution
{
public:
int sum;
int ret;
void dfs(vector<int>& nums, int pos, int path)
{
if (pos == nums.size())
{
if (path == sum)
{
ret++;
}
return;
}
dfs(nums, pos + 1, path + nums[pos]);
dfs(nums, pos + 1, path - nums[pos]);
}
int findTargetSumWays(vector<int>& nums, int target)
{
sum = target;
dfs(nums, 0, 0);
return ret;
}
};
文章来源:https://blog.csdn.net/weixin_74268082/article/details/135165447
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MongoDB认证考试小题库
- TypeScript入门实战笔记 -- 06 类类型:如何高效使用类型化的面向对象编程利器?
- 基于大数据平台(XSailboat)的计算管道实现MySQL数据源的CDC同步--flink CDC
- 数据结构:堆的三部曲(二)top K问题
- C++完成使用map Update数据 二进制数据
- vue前端开发自学,ref为什么称作“钩子”,看完你就明白
- 【QML COOK】- 011-动画插值设置
- Edge浏览器的卸载(一分钟版)
- 《Python数据分析技术栈》第03章 02 数据结构(Structure of data)
- JS手写Promise.all方法