Stable Diffusion - High-Resolution Image Synthesis with Latent Diffusion Models

Paper name

High-Resolution Image Synthesis with Latent Diffusion Models

Paper Reading Note

Paper URL: https://arxiv.org/abs/2112.10752

Code URL: https://github.com/CompVis/latent-diffusion

TL;DR

• 2021 年 runway 和慕尼黑路德维希·马克西米利安大学出品的文章，开源社区大名顶顶的文生图模型 stable diffusion 背后的论文。提出 Latent Diffusion Models，基于 latent space 进行 diffusion，降低计算量需求。

---

Introduction

背景

• 图像生成对计算需求较大，当前一些主流方法的优缺点对比：
  • 自回归（AR）transformer：对于复杂、自然场景的高分辨率图像合成，目前主要是通过（scaling up likelihood-based）概率模型扩展来实现的，这些模型可能包含数十亿参数，参数量较大
  • GAN 的结果主要局限于有限变异性的数据，对抗学习过程不容易扩展到建模复杂、多模态分布
  • Diffusion 模型由一系列去噪自动编码器构成，作为基于似然的模型，没有 GAN 的模式崩溃和训练不稳定性，并且通过参数共享，可以模拟自然图像高度复杂分布，无需像 AR 模型那样涉及数十亿参数
• Diffusion 模型现有问题：
  • 训练和评估模型需要在 RGB 图像这样的高维空间中进行重复的函数评估（和梯度计算），例如，训练最强大的 Diffusion 模型通常需要数百个 GPU 天（例如，在论文 Diffusion Models Beat GANs on Image Synthesis 中为150-1000 个 V100 天）。在输入空间的噪声版本上进行重复评估也使推理变得昂贵，因此在单个A100 GPU上生成50k样本大约需要5天

本文方案

• 提出 Latent Diffusion Models，基于 latent space 进行 diffusion，降低计算量需求
• 出发点来源于对训练好的像素空间 diffusion 模型进行分析：下图展示了一个训练好的模型的速率-失真关系。学习大致可以分为两个阶段：首先是感知压缩阶段，该阶段去除了高频细节，但仍然学到了很少的语义变化。在第二阶段，实际的生成模型学习数据的语义和概念组成（语义压缩）。本文的目标是首先找到一个在感知上等效但在计算上更合适的空间，在这个空间中我们将训练高分辨率图像合成的扩散模型。
  
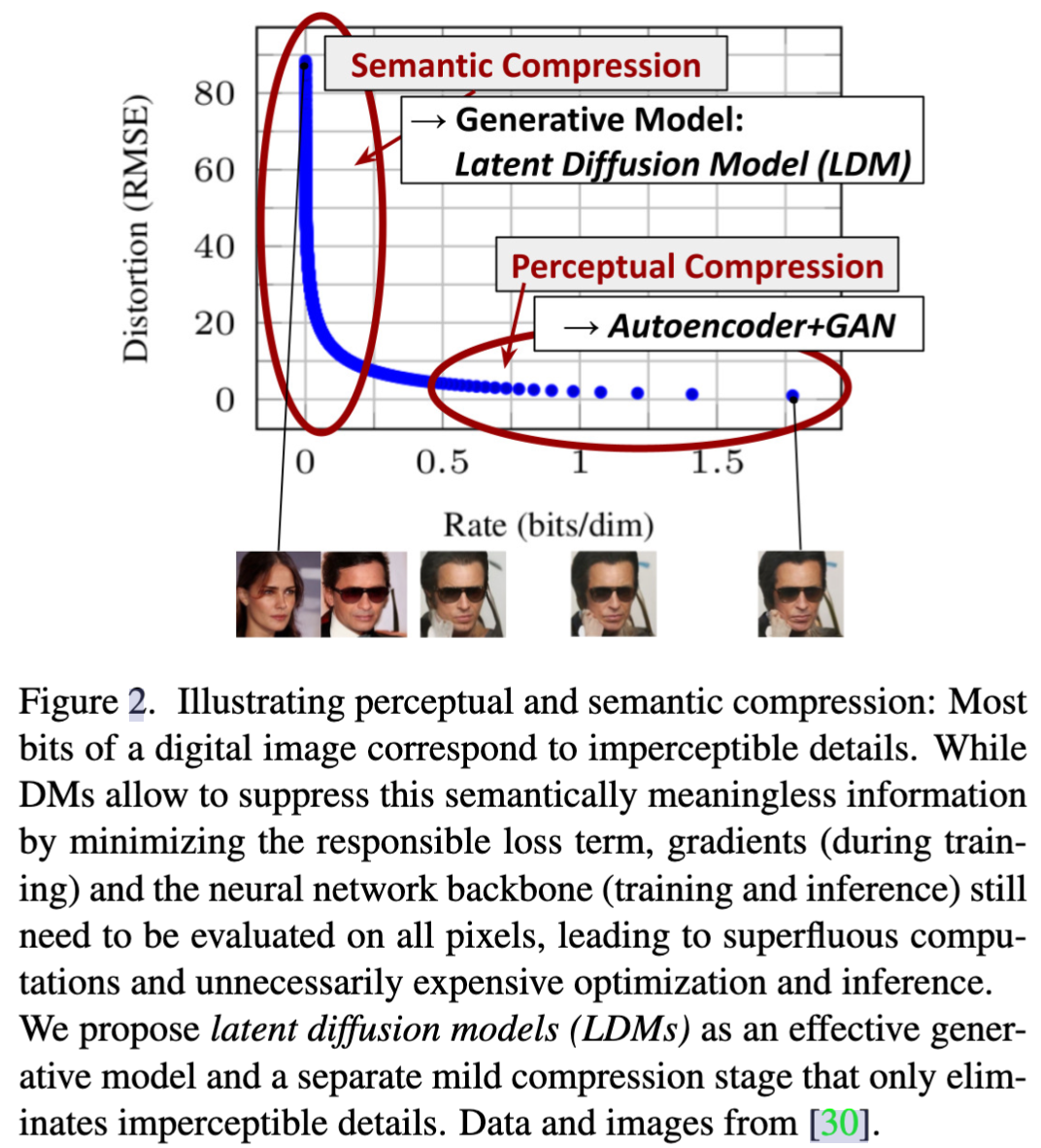
• 本文模型在细节上和指标上优于同时期的 AR 或者 GAN 模型。基于更少的下采样比率实现了更高的效率
  

Methods

• 为了降低训练扩散模型以实现高分辨率图像合成的计算需求，我们观察到，虽然扩散模型通过对应的损失项进行欠采样，允许忽略感知上不相关的细节，但它们仍然需要在像素空间进行昂贵的函数评估，这导致计算时间和能源资源的巨大需求。我们提出通过引入压缩学习和生成学习阶段的显式分离（见图2）来规避这一缺点。为了实现这一点，我们利用一个自动编码模型，该模型学习了一个在感知上等效于图像空间的空间，但具有显著降低的计算复杂性。

Perceptual Image Compression

• 主要基于之前的工作进行，由一个自编码器组成，通过 perceptual loss 和 patch-based 对抗损失进行训练。这确保了通过强制局部真实性，重建被限制在图像流形上，并避免了仅依赖于像素空间损失（如L2或L1目标）引入的模糊性。
• 具体来说
  • 给定一张图片 $x\in {\mathbb{R}}^{H\times W\times 3}$
  • encoder $\epsilon$ 用于将 x 编码到 latent 空间表示： $z=\epsilon (x)$
  • decoder $D$ 用于将 latent 空间重建为图片：$\tilde{x}=D(z)$
  • encoder 下采样率表示为：$f=H/h=W/w=2^m$
• 为了避免潜在空间的任意高方差，尝试了两种不同的正则化方法。
  • 第一种变体 KL-reg.，对学到的 latent 施加了轻微的KL惩罚，朝向标准正态，类似于VAE
  • 第二种变体 VQ-reg. 则在解码器内使用了一个向量量化层。这个模型可以解释为是一个VQGAN，但量化层被吸收到解码器中。
  • 由于我们后续的扩散模型（DM）被设计为使用我们学到的潜在空间 z = E(x) 的二维结构，我们可以使用相对不过度的压缩率并实现非常好的重建。这与先前的工作 VQGAN/DALL-E 形成对比，其依赖于学到的空间 z 的任意 1D 排序来自回归地建模其分布，从而忽略了 z 的许多固有结构。因此，我们的压缩模型更好地保留了 x 的细节（见下表）。
    

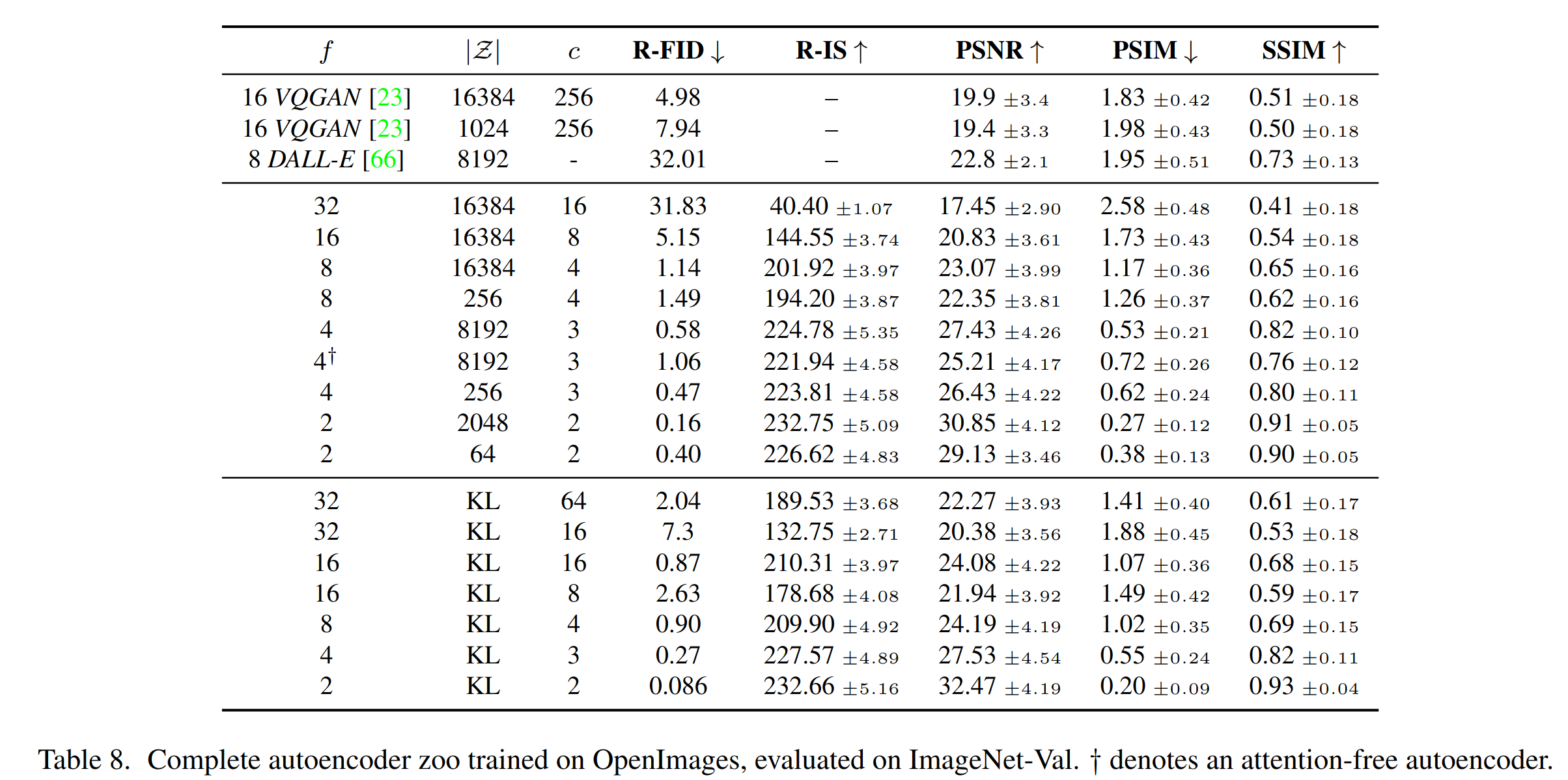
Latent Diffusion Models

扩散模型(DM):

• DM 设计用于通过逐渐去噪一个正态分布变量来学习数据分布 p(x) 的概率模型，这对应于学习长度为 T 的固定马尔可夫链的反向过程。在图像合成方面，最成功的模型 DDPM 等基于对 p(x) 变分下界的一种重新加权变体，这反映了去噪得分匹配。这些模型可以解释为一个等权重的去噪自动编码器序列 $?(x_t,t);t=\mathrm{1...}T$ ，这些自动编码器经过训练以预测其输入 xt 的去噪变体，其中 xt 是输入 x 的带噪声版本。相应的目标可以简化为：
  ${\mathcal{L}}_{\text{DM}}={\mathbb{E}}_{x,?～\mathcal{N}(0,1),t}[\Vert ??{?}_{\theta }(x_t,t){\Vert }_2^2]$
  其中 t 均匀采样自 {1, . . . , T}。

潜在表示的生成建模(Generative Modeling of Latent Representations)

• 利用我们训练得到的感知压缩模型，其中包括 $\epsilon$ 和 $D$，我们现在可以访问一个高效、低维的潜在空间，其中高频、难以察觉的细节被抽象化了。与高维像素空间相比，这个空间更适合基于似然的生成模型，因为它们现在可以

  • （i）专注于数据的重要、语义
  • （ii）在一个更低维、计算效率更高的空间中进行训练。

• 训练目标表示为
  ${\mathcal{L}}_{\text{LDM}}:={\mathbb{E}}_{E(x),?～\mathcal{N}(0,1),t}[\Vert ??{?}_{\theta }(z_t,t){\Vert }_2^2].$

• 我们模型的神经骨架 $?(?,t)$ 实现为一个时态条件(time-conditional) UNet。由于正向过程是固定的，在训练过程中可以有效地从 $\epsilon$ 获取 $z_t$，并且从 $p(z)$ 中解码的样本可以通过一次 $D$ 的传递转换回图像空间。

Conditioning Mechanisms

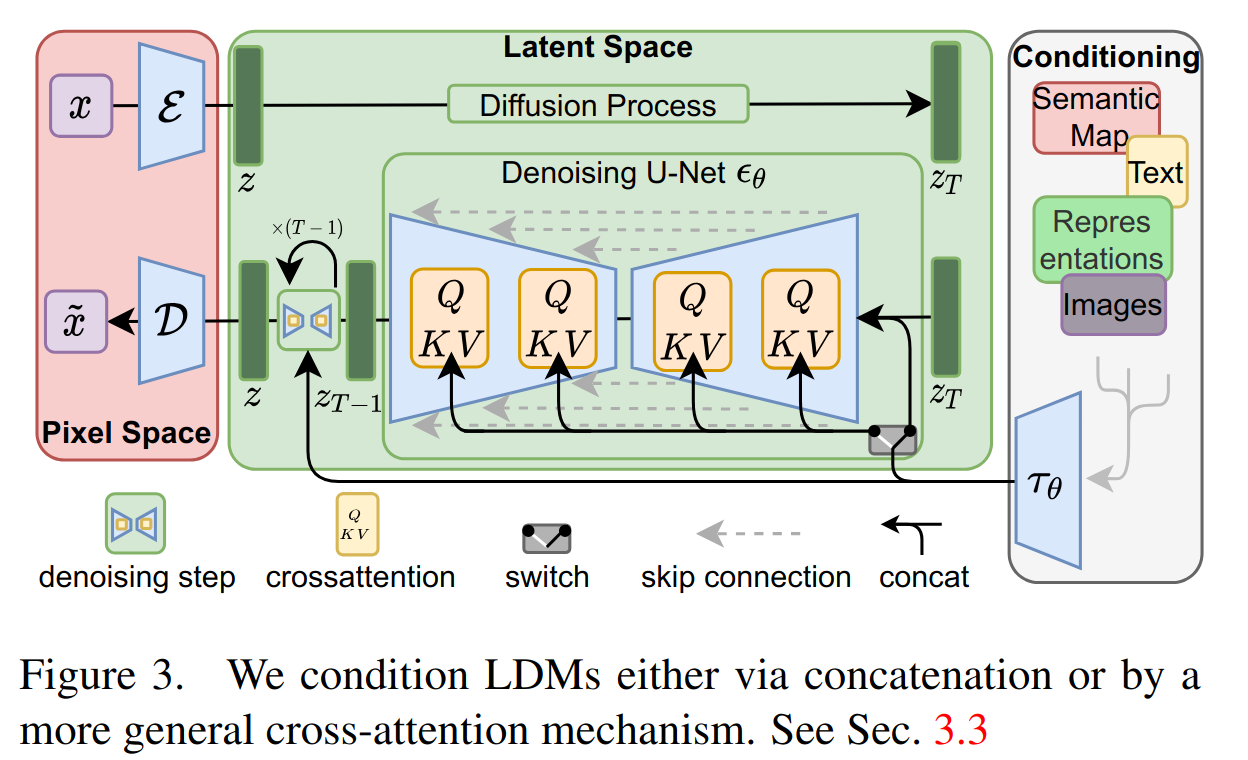
• 类似于其他类型的生成模型 (CGAN)，扩散模型原则上能够建模形式为 $p(z|y)$ 的条件分布。这可以通过使用条件去噪自动编码器 $?(z_t,t,y)$ 来实现，并为通过输入 y（如文本、语义地图或其他图像到图像翻译任务）控制合成。然而，在图像合成的背景下，将 DMs 的生成能力与超出类别标签或输入图像的模糊变体之外的其他类型的条件结合起来，迄今为止仍是一个未充分探讨的研究领域。我们通过在 DMs 的基础 UNet 骨干上增加交叉注意力机制将 DMs 转化为更灵活的条件图像生成器。
• 为了预处理来自各种模态的 y（例如语言提示），我们引入了一个领域特定的编码器 ${\tau }_{\theta }$，将 y 投影到一个中间表示 ${\tau }_{\theta }(y)\in {\mathbb{R}}^{M\times d_{\tau }}$ ，然后通过以下的交叉注意力机制实现将 ${\tau }_{\theta }(y)$ 映射到 UNet 的中间层：
  $Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d}})?V$
  其中 $Q=W_Q^{(i)}?{\phi }_i(zt)$，$K=W_K^{(i)}?{\tau }_{\theta }(y)$，$V=W_V^{(i)}?{\tau }_{\theta }(y)$。在这里，${\phi }_i(zt)\in {\mathbb{R}}^{N\times di}$ 代表 UNet 实现 ${?}_{\theta }$ 的（flattened）中间表示，$W_V^{(i)}\in {\mathbb{R}}^{d\times d_i}$，$W_Q^{(i)}\in R^d\times d\tau$ 和 $W_K^{(i)}\in {\mathbb{R}}^{d\times d_{\tau }}$ 是可学习的投影矩阵。见图 3 进行视觉描述。基于图像条件对，然后通过以下方式学习条件 LDM：
  ${\mathcal{L}}_{\text{LDM}}:={\mathbb{E}}_{\epsilon (x),y,?～\mathcal{N}(0,1),t}[\Vert ??{?}_{\theta }(z_t,t,{\tau }_{\theta }(y)){\Vert }_2^2]$
  其中 ${\tau }_{\theta }$ 和 ${?}_{\theta }$ 通过上面的目标函数联合优化。这个条件机制是灵活的，因为 ${\tau }_{\theta }$ 可以用领域特定的模型进行初始化。

Experiments

• 首先，我们将分析我们的模型在训练和推断中与基于像素的扩散模型相比的优势。有趣的是，我们发现在 VQ 正则化的潜在空间中训练的 LDMs 有时能够实现更好的样本质量，即使相较于连续版本，VQ 正则化的第一阶段模型的重建能力（reconstruction capabilities）略微落后，参见上述的表 8。
• 关于第一阶段正则化方案对 LDM 训练的影响以及它们对分辨率 > 256^2 的泛化能力的视觉比较如下
  
  由潜在空间的方差引起的信噪比（即 $Var(z)/{\sigma }_t^2$）对卷积采样的结果有显著影响。例如，当直接在一个KL正则化模型的潜在空间中训练 LDM 时，这个比率非常高，以至于模型在反向去噪过程的早期分配了大量的语义细节。相反，当通过潜在变量的逐分量标准差对潜在空间进行重新缩放时，信噪比降低。我们在上图中说明了这对语义图像合成中卷积采样的影响。请注意，VQ 正则化空间的方差接近1，因此不需要重新缩放。

On Perceptual Compression Tradeoffs

• 本节分析了我们的LDMs在不同的下采样因子f ∈ {1, 2, 4, 8, 16, 32}（简写为LDM-f，其中LDM-1对应于基于像素的DMs）的行为。为了获得可比较的测试场，我们将计算资源固定为单个NVIDIA A100，并在本节的所有实验中以相同数量的步骤和相同数量的参数对所有模型进行训练。
  

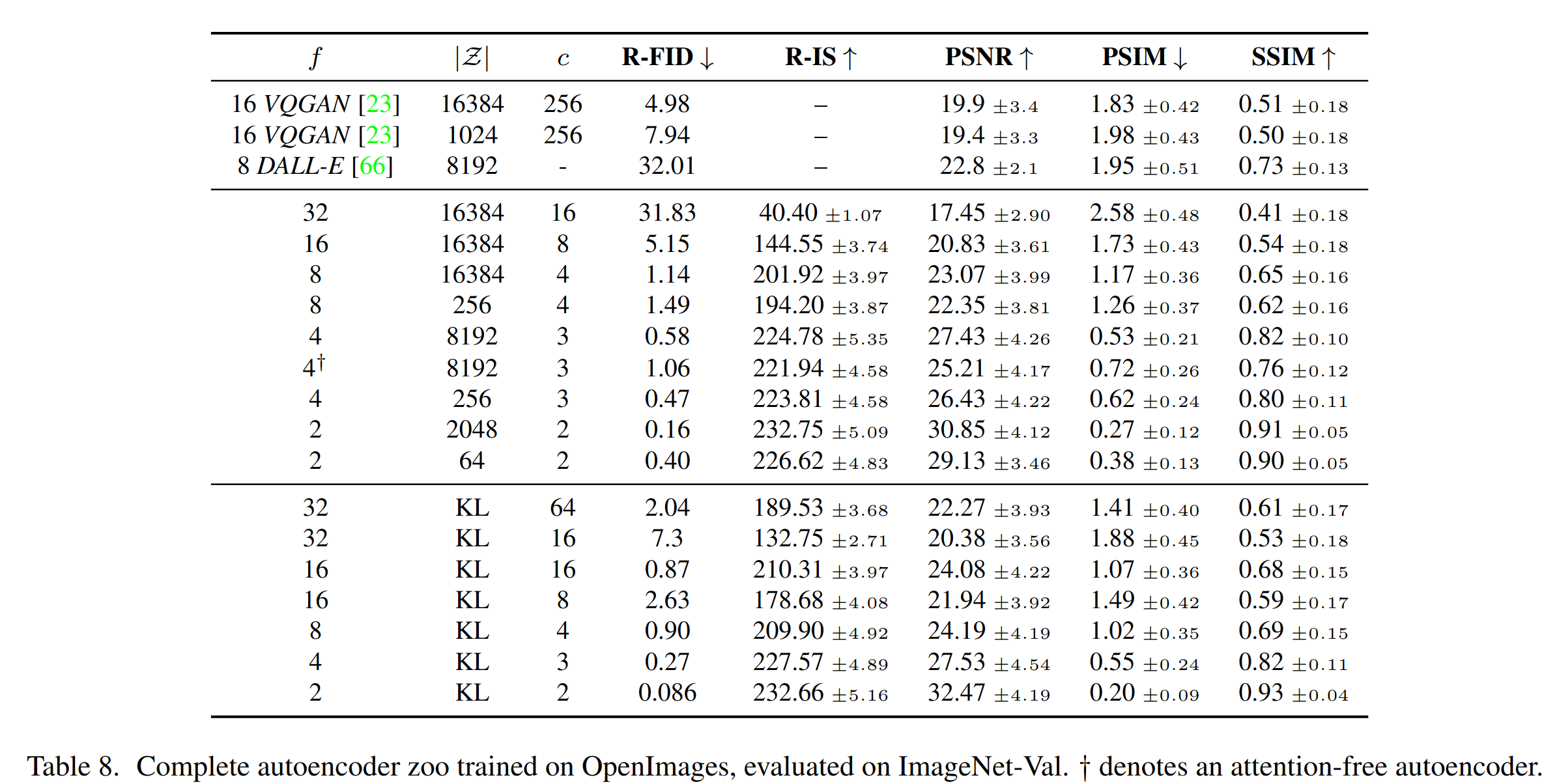
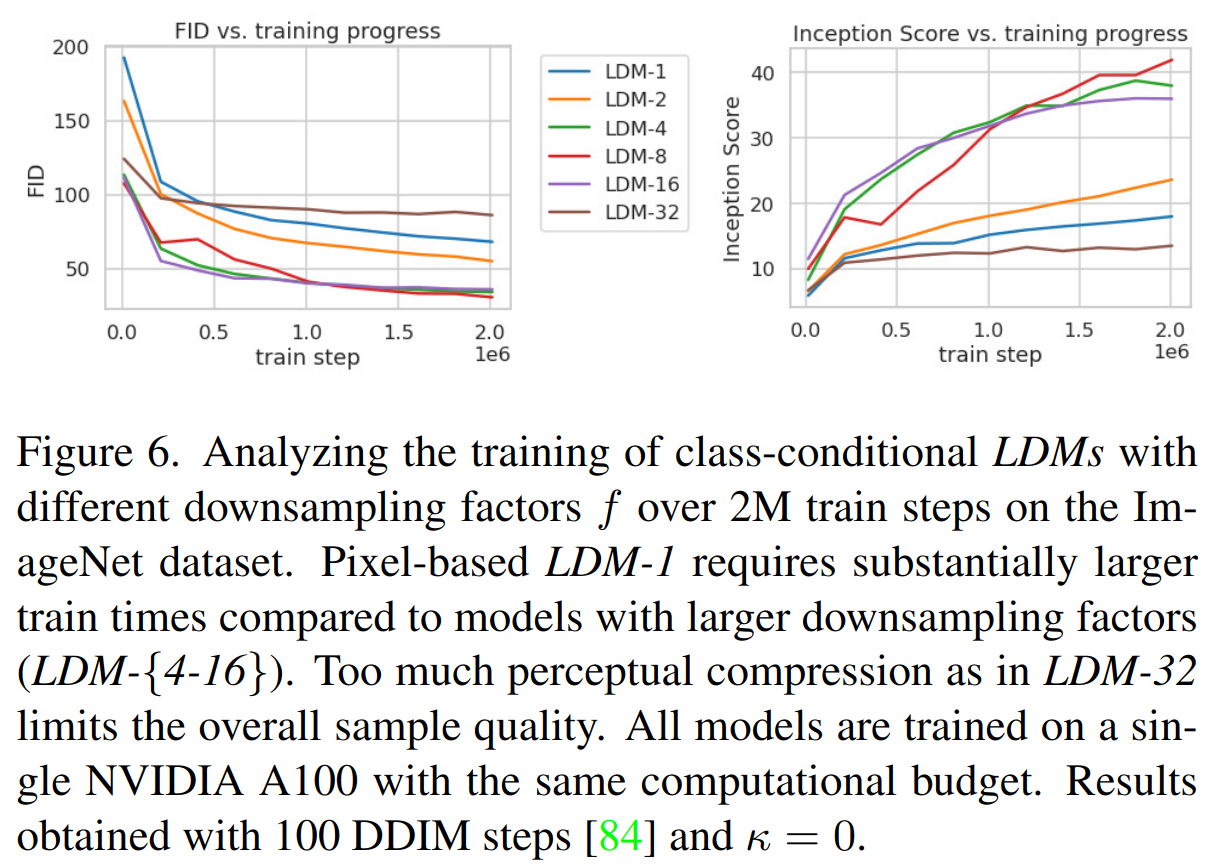
• ImageNet 数据集上进行了 2M 步类别条件模型训练的样本质量随训练进展的变化如下，LDM-{4-16}在效率和感知上忠实的结果之间取得了良好的平衡：

  • i) 对于LDM-{1,2}来说，小的下采样因子导致训练进展缓慢。作者认为原因是将大部分感知压缩留给扩散模型
  • ii) 过大的 f 值导致在相对较少的训练步骤后保真度停滞。作者认为原因是过强的第一阶段压缩导致信息丢失，从而限制了可实现的质量

• 比较了在 CelebAHQ 和 ImageNet 上训练的模型，针对 DDIM 采样器的不同去噪步骤数量，将其与FID分数绘制在一起。LDM-{4-8} 在感知和概念压缩的不合适比率方面优于其他模型
  

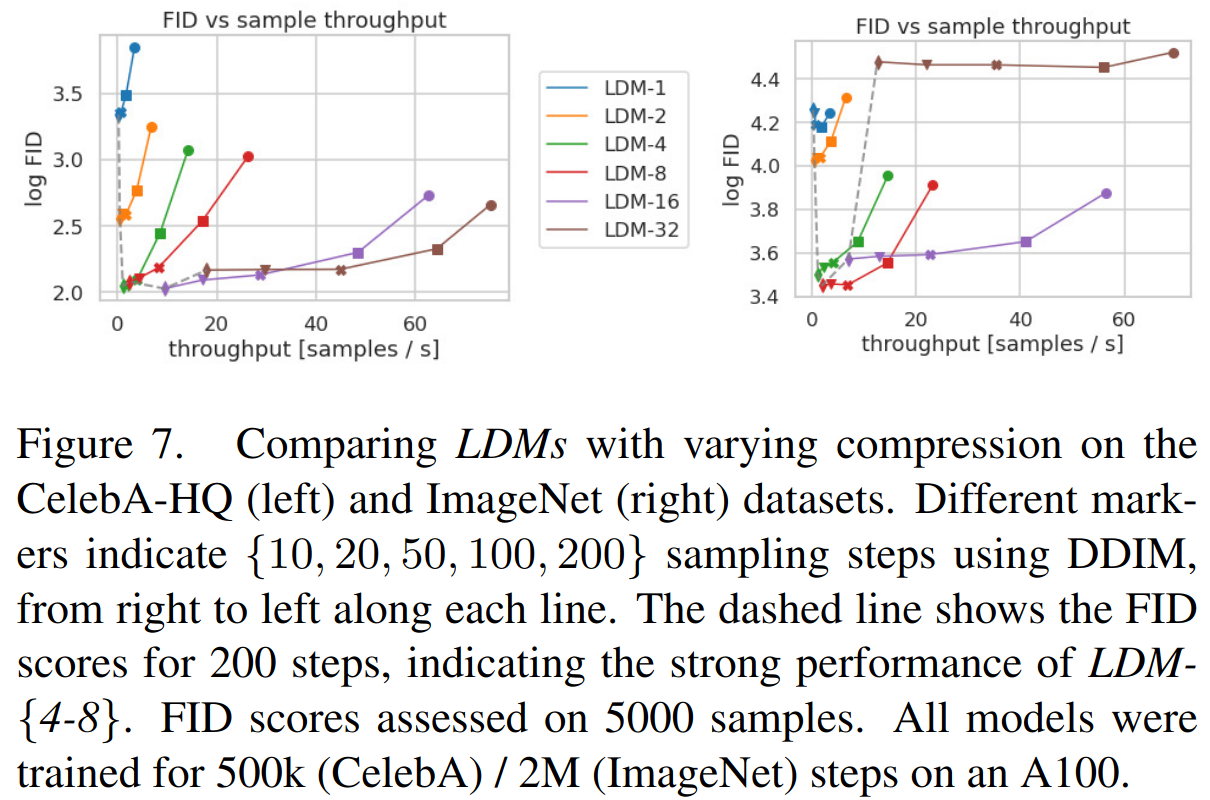
Image Generation with Latent Diffusion

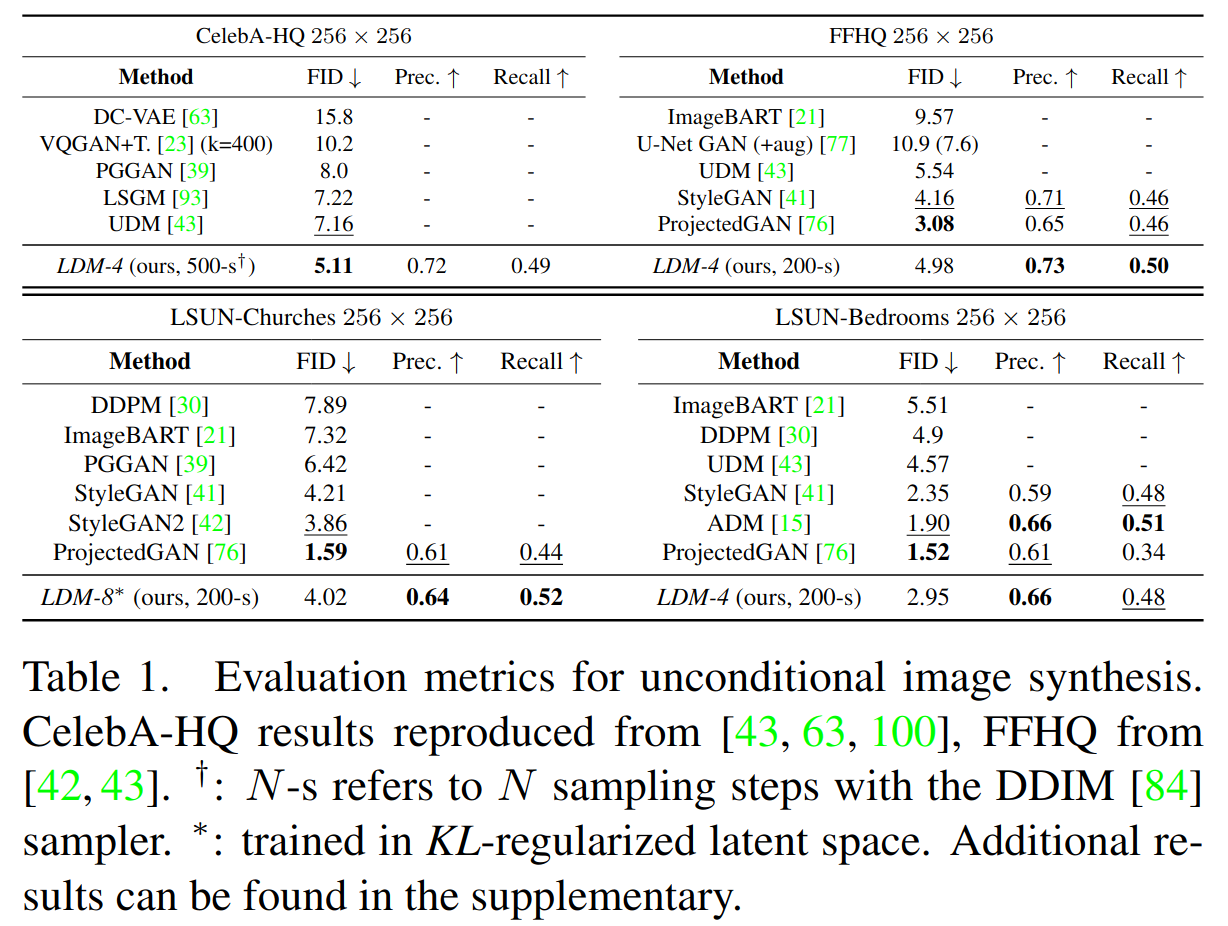
• 在 CelebA-HQ、FFHQ、LSUN-Churches 和 Bedrooms 上训练了 256^2 图像的无条件模型，并评估了它们的 i) 样本质量和 ii) 对数据流形的覆盖，使用 ii) FID 和 ii) 精度与召回指标进行评测。在CelebA-HQ上，我们报告了一个新的FID记录，为5.11，超过了先前基于似然的模型以及GANs
  
• 生成效果如下
  

Conditional Latent Diffusion

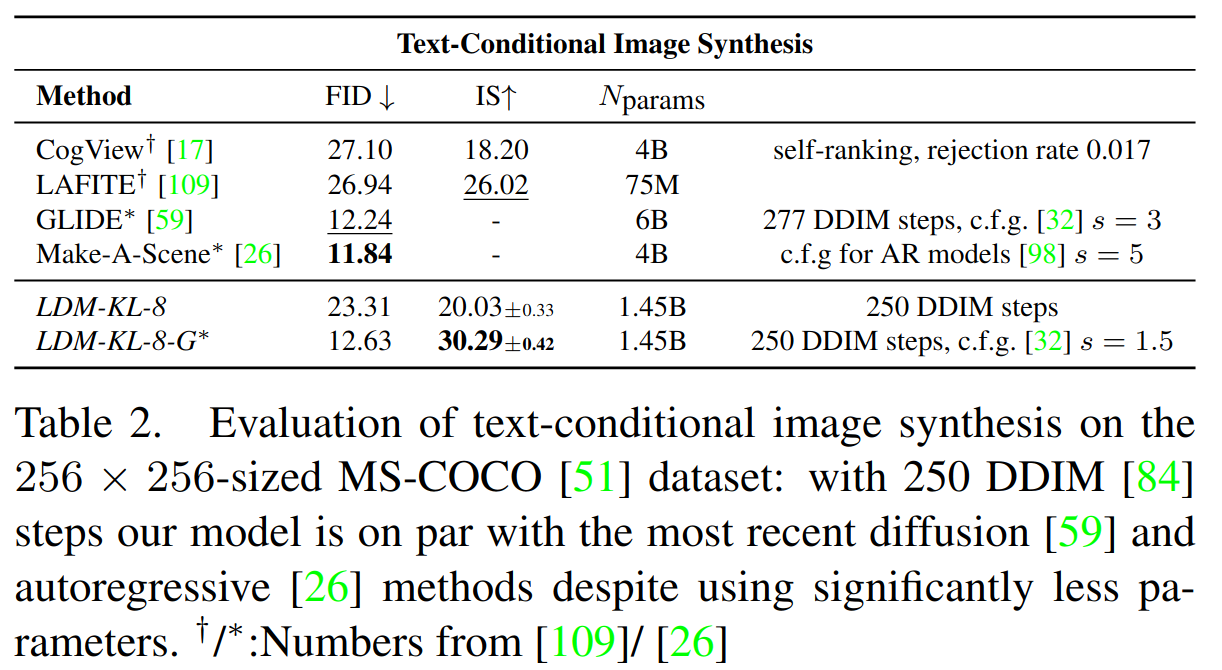
• 实现方式：对于文本到图像建模，我们在 LAION-400M 上训练了一个具有 1.45B 参数的 KL 正则化的 LDM，该模型以语言提示为条件

  • 使用BERT-tokenizer，并将 ${\tau }_{\theta }$ 实现为一个 transformer，以推断一个潜在特征，该特征通过（多头）交叉注意力映射到 UNet

• COCO 上的定量分析结果，classifier-free diffusion guidance 极大提升质量。使用 guide 的 LDM-KL-8-G 基本能基本媲美 AR 方法 Make-A-Scene 和 diffusion 方法 GLIDE
  

• 基于文本作为条件
  

• 基于检测框和文本作为条件
  

• 基于语义分割图作为条件
  

超分应用

• 低分辨率图片作为条件训练，即可进行超分操作
  

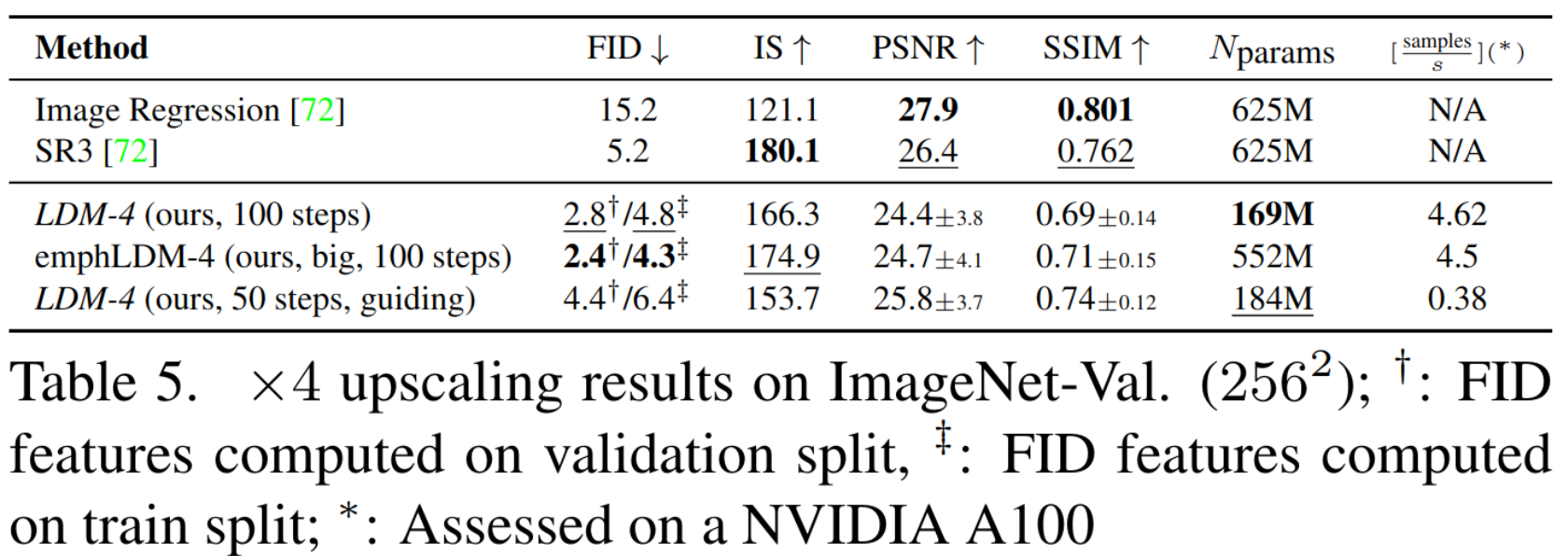
inpainting 应用

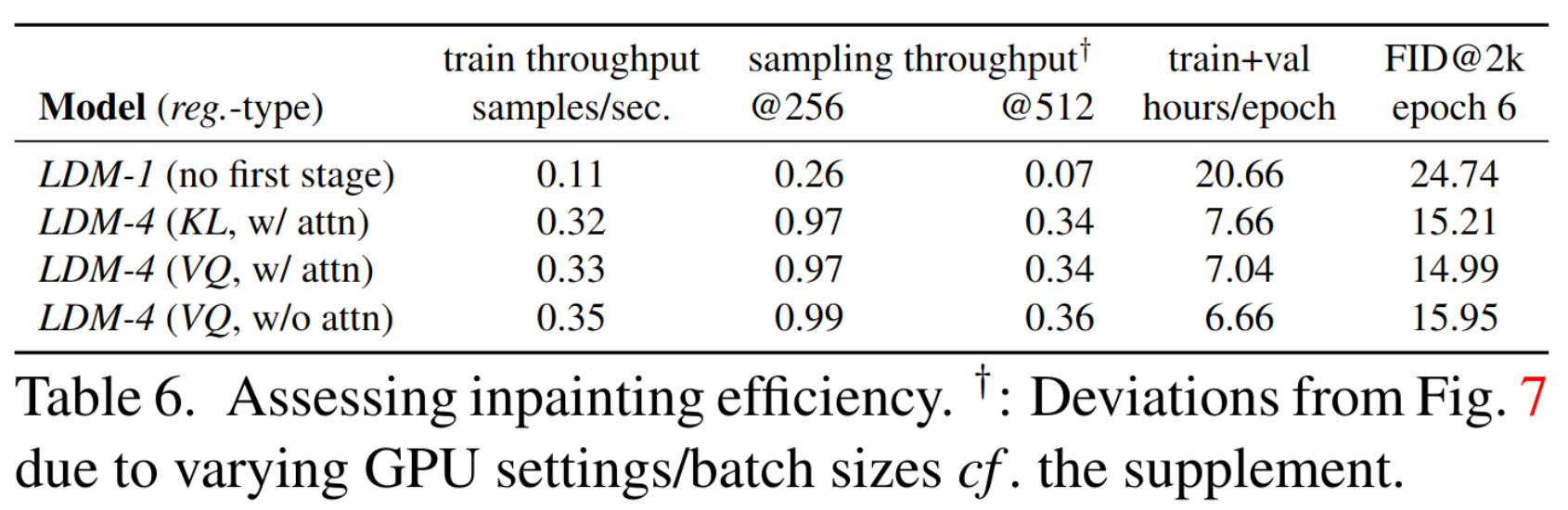
Thoughts

• 比较早期的经典工作，实验非常详尽，将 diffusion 开源效果推到新的高度