PriorityBlockingQueue概念

四、PriorityBlockingQueue概念

4.1 PriorityBlockingQueue介绍

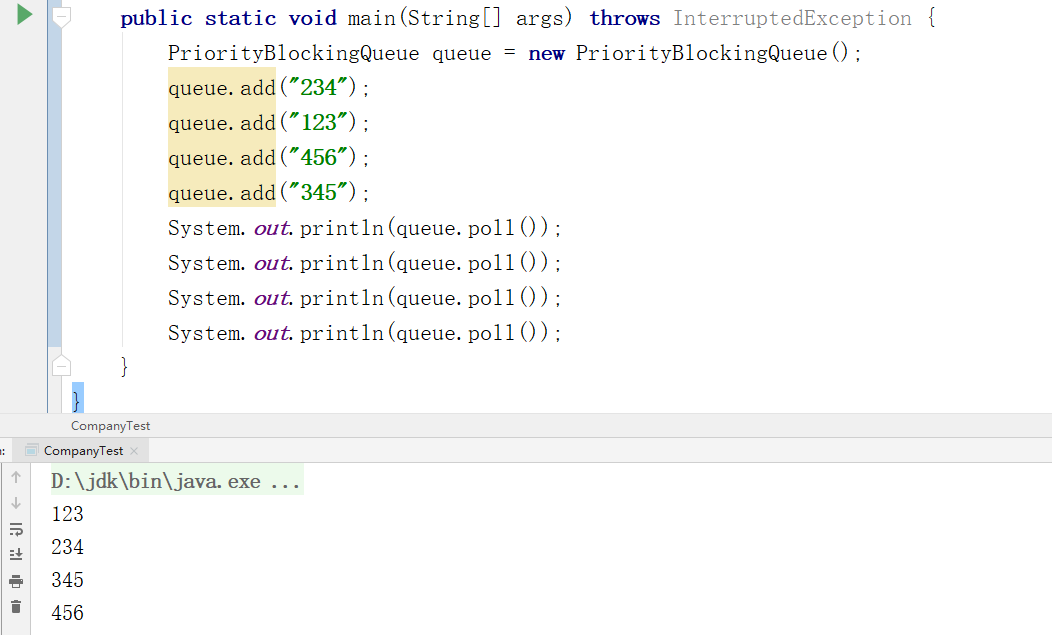
首先PriorityBlockingQueue是一个优先级队列，他不满足先进先出的概念。

会将查询的数据进行排序，排序的方式就是基于插入数据值的本身。

如果是自定义对象必须要实现Comparable接口才可以添加到优先级队列

排序的方式是基于二叉堆实现的。底层是采用数据结构实现的二叉堆。

4.2 二叉堆结构介绍

优先级队列PriorityBlockingQueue基于二叉堆实现的。

private transient Object[] queue;

PriorityBlockingQueue是基于数组实现的二叉堆。

二叉堆是什么？

• 二叉堆就是一个完整的二叉树。
• 任意一个节点大于父节点或者小于父节点
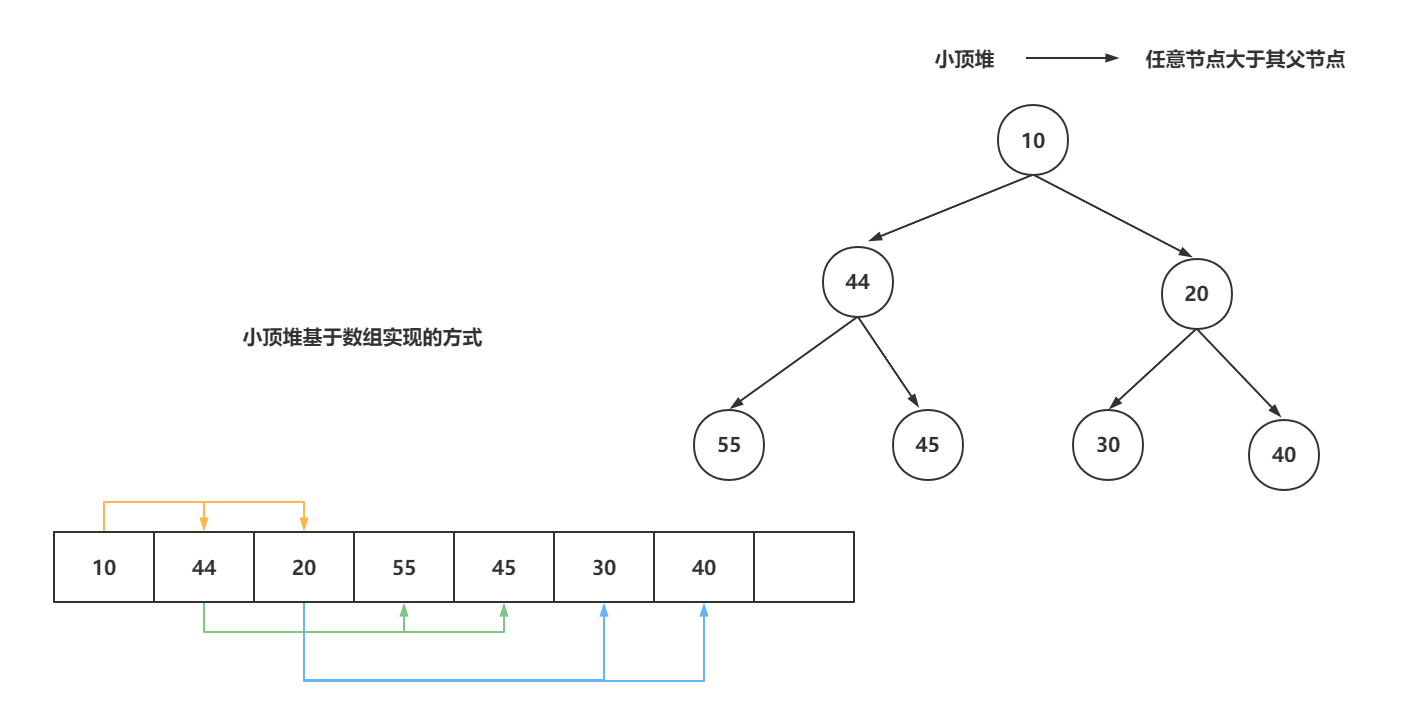
• 基于同步的方式，可以定义出小顶堆和大顶堆

小顶堆以及小顶堆基于数据实现的方式。

4.3 PriorityBlockingQueue核心属性

// 数组的初始长度
private static final int DEFAULT_INITIAL_CAPACITY = 11;

// 数组的最大长度
// -8的目的是为了适配各个版本的虚拟机
// 默认当前使用的hotspot虚拟机最大支持Integer.MAX_VALUE - 2，但是其他版本的虚拟机不一定。
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

// 存储数据的数组，也是基于这个数组实现的二叉堆。
private transient Object[] queue;

// size记录当前阻塞队列中元素的个数
private transient int size;

// 要求使用的对象要实现Comparable比较器。基于comparator做对象之间的比较
private transient Comparator<? super E> comparator;

// 实现阻塞队列的lock锁
private final ReentrantLock lock;

// 挂起线程操作。
private final Condition notEmpty;

// 因为PriorityBlockingQueue的底层是基于二叉堆的，而二叉堆又是基于数组实现的，数组长度是固定的，如果需要扩容，需要构建一个新数组。PriorityBlockingQueue在做扩容操作时，不会lock住的，释放lock锁，基于allocationSpinLock属性做标记，来避免出现并发扩容的问题。
private transient volatile int allocationSpinLock;

// 阻塞队列中用到的原理，其实就是普通的优先级队列。
private PriorityQueue<E> q;

4.4 PriorityBlockingQueue的写入操作

毕竟是阻塞队列，添加数据的操作，咱们是很了解，无法还是add，offer，offer(time,unit)，put。但是因为优先级队列中，数组是可以扩容的，虽然有长度限制，但是依然属于无界队列的概念，所以生产者不会阻塞，所以只有offer方法可以查看。

这次核心的内容并不是添加数据的区别。主要关注的是如何保证二叉堆中小顶堆的结构的，并且还要查看数组扩容的一个过程是怎样的。

4.4.1 offer基本流程

因为add方法依然调用的是offer方法，直接查看offer方法即可

public boolean offer(E e) {
    // 非空判断。
    if (e == null)
        throw new NullPointerException();
    // 拿到锁，直接上锁
    final ReentrantLock lock = this.lock;
    lock.lock();
    // n：size，元素的个数
    // cap：当前数组的长度
    // array：就是存储数据的数组
    int n, cap;
    Object[] array;
    while ((n = size) >= (cap = (array = queue).length))
        // 如果元素个数大于等于数组的长度，需要尝试扩容。
        tryGrow(array, cap);
    try {
        // 拿到了比较器
        Comparator<? super E> cmp = comparator;
        // 比较数据大小，存储数据，是否需要做上移操作，保证平衡的
        if (cmp == null)
            siftUpComparable(n, e, array);
        else
            siftUpUsingComparator(n, e, array, cmp);
        // 元素个数 + 1
        size = n + 1;
        // 如果有挂起的线程，需要去唤醒挂起的消费者。
        notEmpty.signal();
    } finally {
        // 释放锁
        lock.unlock();
    }
    // 返回true
    return true;
}

4.4.2 offer扩容操作

在添加数据之前，会采用while循环的方式，来判断当前元素个数是否大于等于数组长度。如果满足，需要执行tryGrow方法，对数组进行扩容

如果两个线程同时执行tryGrow，只会有一个线程在扩容，另一个线程可能多次走while循环，多次走tryGrow方法，但是依然需要等待前面的线程扩容完毕。

private void tryGrow(Object[] array, int oldCap) {
    // 释放锁资源。
    lock.unlock(); 
    // 声明新数组。
    Object[] newArray = null;
    // 如果allocationSpinLock属性值为0，说明当前没有线程正在扩容的。
    if (allocationSpinLock == 0 &&
        // 基于CAS的方式，将allocationSpinLock从0修改为1，代表当前线程可以开始扩容
        UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,0, 1)) {
        try {
            // 计算新数组长度
            int newCap = oldCap + ((oldCap < 64) ?
                                   // 如果数组长度比较小，这里加快扩容长度速度。
                                   (oldCap + 2) : 
                                   // 如果长度大于等于64了，每次扩容到1.5倍即可。
                                   (oldCap >> 1));
            // 如果新数组长度大于MAX_ARRAY_SIZE，需要做点事了。
            if (newCap - MAX_ARRAY_SIZE > 0) {   
                // 声明minCap，长度为老数组 + 1
                int minCap = oldCap + 1;
                // 老数组+1变为负数，或者老数组长度已经大于MAX_ARRAY_SIZE了，无法扩容了。
                if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
                    // 告辞，凉凉~~~~
                    throw new OutOfMemoryError();
                // 如果没有超过限制，直接设置为最大长度即可
                newCap = MAX_ARRAY_SIZE;
            }
            // 新数组长度，得大于老数组长度，
            // 第二个判断确保没有并发扩容的出现。
            if (newCap > oldCap && queue == array)
                // 构建出新数组
                newArray = new Object[newCap];
        } finally {
            // 新数组有了，标记位归0~~
            allocationSpinLock = 0;
        }
    }
    // 如果到了这，newArray依然为null，说明这个线程没有进到if方法中，去构建新数组
    if (newArray == null) 
        // 稍微等一手。
        Thread.yield();
    // 拿锁资源，
    lock.lock();
    // 拿到锁资源后，确认是构建了新数组的线程，这里就需要将新数组复制给queue，并且导入数据
    if (newArray != null && queue == array) {
        // 将新数组赋值给queue
        queue = newArray;
        // 将老数组的数据全部导入到新数组中。
        System.arraycopy(array, 0, newArray, 0, oldCap);
    }
}

4.4.3 offer添加数据

这里是数据如何放到数组上，并且如何保证的二叉堆结构

// k：当前元素的个数（其实就是要放的索引位置）
// x：需要添加的数据
// array：数组。。
private static <T> void siftUpComparable(int k, T x, Object[] array) {
    // 将插入的元素直接强转为Comparable（com.mashibing.User cannot be cast to java.lang.Comparable）
    // 这行强转，会导致添加没有实现Comparable的元素，直接报错。
    Comparable<? super T> key = (Comparable<? super T>) x;
    // k大于0，走while逻辑。（原来有数据）
    while (k > 0) {
        // 获取父节点的索引位置。
        int parent = (k - 1) >>> 1;
        // 拿到父节点的元素。
        Object e = array[parent];
        // 用子节点compareTo父节点，如果 >= 0，说明当前son节点比parent要大。
        if (key.compareTo((T) e) >= 0)
            // 直接break，完事，
            break;
        // 将son节点的位置设置上之前的parent节点
        array[k] = e;
        // 重新设置x节点需要放置的位置。
        k = parent;
    }
    // k == 0，当前元素是第一个元素，直接插入进去。
    array[k] = key;
}

4.5 PriorityBlockingQueue的读取操作

读取操作是存储现在挂起的情况的，因为如果数组中元素个数为0，当前线程如果执行了take方法，必然需要挂起。

其次获取数据，因为是优先级队列，所以需要从二叉堆栈顶拿数据，直接拿索引为0的数据即可，但是拿完之后，需要保持二叉堆结构，所以会有下移操作。

4.5.1 查看获取方法流程

poll：

public E poll() {
    final ReentrantLock lock = this.lock;
    // 加锁
    lock.lock();
    try {
        // 拿到返回数据，没拿到，返回null
        return dequeue();
    } finally {
        lock.unlock();
    }
}

poll(time,unit)：

public E poll(long timeout, TimeUnit unit) throws InterruptedException {
    // 将挂起的时间转换为纳秒
    long nanos = unit.toNanos(timeout);
    final ReentrantLock lock = this.lock;
    // 允许线程中断抛异常的加锁
    lock.lockInterruptibly();
    // 声明结果
    E result;
    try {
        // dequeue是去拿数据的，可能会出现拿到的数据为null，如果为null，同时挂起时间还有剩余，这边就直接通过notEmpty挂起线程
        while ( (result = dequeue()) == null && nanos > 0)
            nanos = notEmpty.awaitNanos(nanos);
    } finally {
        lock.unlock();
    }
    // 有数据正常返回，没数据，告辞~
    return result;
}

take：

public E take() throws InterruptedException {
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    E result;
    try {
        while ( (result = dequeue()) == null)
            // 无线等，要么有数据，要么中断线程
            notEmpty.await();
    } finally {
        lock.unlock();
    }
    return result;
}

4.5.2 查看dequeue获取数据

获取数据主要就是从数组中拿到0索引位置数据，然后保持二叉堆结构

private E dequeue() {
    // 将元素个数-1，拿到了索引位置。
    int n = size - 1;
    // 判断是不是木有数据了，没数据直接返回null即可
    if (n < 0)
        return null;
    // 说明有数据
    else {
        // 拿到数组，array
        Object[] array = queue;
        // 拿到0索引位置的数据
        E result = (E) array[0];
        // 拿到最后一个数据
        E x = (E) array[n];
        // 将最后一个位置置位null
        array[n] = null;
        Comparator<? super E> cmp = comparator;
        if (cmp == null)
            siftDownComparable(0, x, array, n);
        else
            siftDownUsingComparator(0, x, array, n, cmp);
        // 元素个数-1，赋值size
        size = n;
        // 返回result
        return result;
    }
}

4.6.3 下移做平衡操作

一定要以局部的方式去查看树结构的变化，他是从跟节点往下找较小的一个子节点，将较小的子节点挪动到父节点位置，再将循环往下走，如果一来，整个二叉堆的结构就可以保证了。

// k：默认进来是0
// x：代表二叉堆的最后一个数据
// array：数组
// n：最后一个索引
private static <T> void siftDownComparable(int k, T x, Object[] array,int n) {
    // 健壮性校验，取完第一个数据，已经没数据了，那就不需要做平衡操作
    if (n > 0) {
        // 拿到最后一个数据的比较器
        Comparable<? super T> key = (Comparable<? super T>)x;
        // 因为二叉堆是一个二叉满树，所以在保证二叉堆结构时，只需要做一半就可以
        int half = n >>> 1; 
        // 做了超过一半，就不需要再往下找了。
        while (k < half) {
            // 找左子节点索引，一个公式，可以找到当前节点的左子节点
            int child = (k << 1) + 1; 
            // 拿到左子节点的数据
            Object c = array[child];
            // 拿到右子节点索引
            int right = child + 1;
            // 确认有右子节点
            // 判断左节点是否大于右节点
            if (right < n && c.compareTo(array[right]) > 0)
                // 如果左大于右，那么c就执行右
                c = array[child = right];
            // 比较最后一个节点是否小于当前的较小的子节点
            if (key.compareTo((T) c) <= 0)
                break;
            // 将左右子节点较小的放到之前的父节点位置
            array[k] = c;
            // k重置到之前的子节点位置
            k = child;
        }
        // 上面while循环搞定后，可以确认整个二叉堆中，数据已经移动ok了，只差当前k的位置数据是null
        // 将最后一个索引的数据放到k的位置
        array[k] = key;
    }
}