【MATLAB】鲸鱼算法优化混合核极限学习机(WOA-HKELM)时序预测算法
有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义
鲸鱼算法优化混合核极限学习机(WOA-HKELM)是一种时序预测算法,它结合了鲸鱼算法和混合核极限学习机(HKELM)的优点。以下是该算法的基本原理:
-
「初始化」:在算法开始时,需要在可行解空间中初始化一群鲸鱼个体。每个鲸鱼个体代表一个潜在的最优解,位置表示鲸鱼的特征,适应度值由适应度函数计算得到。
-
「搜索」:每个鲸鱼按照一定的规则探索空间。这个过程模拟了鲸鱼包围、追捕和攻击猎物等过程。具体来说,每只鲸鱼会根据其当前位置和速度,按照一定的规则在解空间中移动,并更新其位置。
-
「评估」:每当鲸鱼移动时,都会计算当前的适应度值。适应度值由目标函数计算得到,表示鲸鱼的优劣。如果当前的适应度值优于之前的适应度值,则将当前适应度值设为最优解。
-
「更新」:当所有的鲸鱼都完成移动和评估后,算法会根据一定的规则更新所有鲸鱼的位置和速度。更新的规则是基于鲸鱼的适应度值和种群最优解的情况,确保算法向着更优的方向演化。
-
「迭代」:重复上述步骤,直到满足终止条件或者达到预设的最大迭代次数。在迭代过程中,鲸鱼的主要行为包括包围猎物、捕获猎物、搜索猎物等。通过这些行为,鲸鱼种群逐渐向最优解靠近。
通过以上步骤,鲸鱼算法优化混合核极限学习机(WOA-HKELM)能够找到最优解,实现时序预测。该算法具有较高的效率和稳定性,能够应用于各种类型的优化问题。
在WOA-HKELM中,HKELM被用作预测模型,而鲸鱼算法被用于优化HKELM的参数。通过优化参数,WOA-HKELM能够提高预测精度和稳定性。
总的来说,WOA-HKELM 是一种非常实用的时序预测工具,尤其适合新手学习和研究人员进行时序预测的实验和比较。在实际应用中,通过调整参数和优化算法,WOA-HKELM 工具也能够满足不同场景和任务的需求。
以下是对鲸鱼算法优化混合核极限学习机(WOA-HKELM)实现过程的描述:
-
「初始化」:在算法开始时,需要在可行解空间中初始化一群鲸鱼个体。每个鲸鱼个体代表一个潜在的最优解,位置表示鲸鱼的特征,适应度值由适应度函数计算得到。
-
「搜索」:每个鲸鱼按照一定的规则探索空间。这个过程模拟了鲸鱼包围、追捕和攻击猎物等过程。具体来说,每只鲸鱼会根据其当前位置和速度,按照一定的规则在解空间中移动,并更新其位置。
-
「评估」:每当鲸鱼移动时,都会计算当前的适应度值。适应度值由目标函数计算得到,表示鲸鱼的优劣。如果当前的适应度值优于之前的适应度值,则将当前适应度值设为最优解。
-
「更新」:当所有的鲸鱼都完成移动和评估后,算法会根据一定的规则更新所有鲸鱼的位置和速度。更新的规则是基于鲸鱼的适应度值和种群最优解的情况,确保算法向着更优的方向演化。
-
「迭代」:重复上述步骤,直到满足终止条件或者达到预设的最大迭代次数。在迭代过程中,鲸鱼的主要行为包括包围猎物、捕获猎物、搜索猎物等。通过这些行为,鲸鱼种群逐渐向最优解靠近。
通过以上步骤,鲸鱼算法优化混合核极限学习机(WOA-HKELM)能够找到最优解,实现时序预测。该算法具有较高的效率和稳定性,能够应用于各种类型的优化问题。
在鲸鱼优化算法(WOA)中,参数的调整可以通过实验和经验来决定。以下是一些常见的参数调整方法:
-
「种群规模」:种群规模是指算法中鲸鱼的数量,通常需要通过实验来选择合适的种群规模。一般来说,种群规模不宜过大或过小,需要根据问题的复杂性和求解精度要求进行合理设置。
-
「迭代次数」:迭代次数是指算法的迭代次数,也需要在实验中进行合理设置。如果迭代次数太少,算法可能无法找到全局最优解;如果迭代次数太多,可能会导致算法运行时间过长。
-
「搜索空间」:搜索空间是指鲸鱼在解空间中移动的范围,可以通过设置适当的搜索空间来限制鲸鱼的移动范围。搜索空间的设置需要根据问题的特性进行合理设置。
-
「学习因子」:学习因子是指鲸鱼之间的学习程度,可以通过调整学习因子的值来影响算法的性能。一般来说,学习因子的值应该在一定范围内进行选择,以便在全局搜索和局部搜索之间取得平衡。
-
「边界条件」:边界条件是指解空间的边界,可以通过设置合理的边界条件来避免鲸鱼越界。边界条件的设置应该根据问题的实际情况进行合理设置。
在调整参数时,可以尝试不同的参数组合,通过实验和比较来选择最优的参数配置。同时,也可以参考其他优化算法的参数调整经验,以便更好地优化鲸鱼优化算法的性能。
2 出图效果
附出图效果如下:



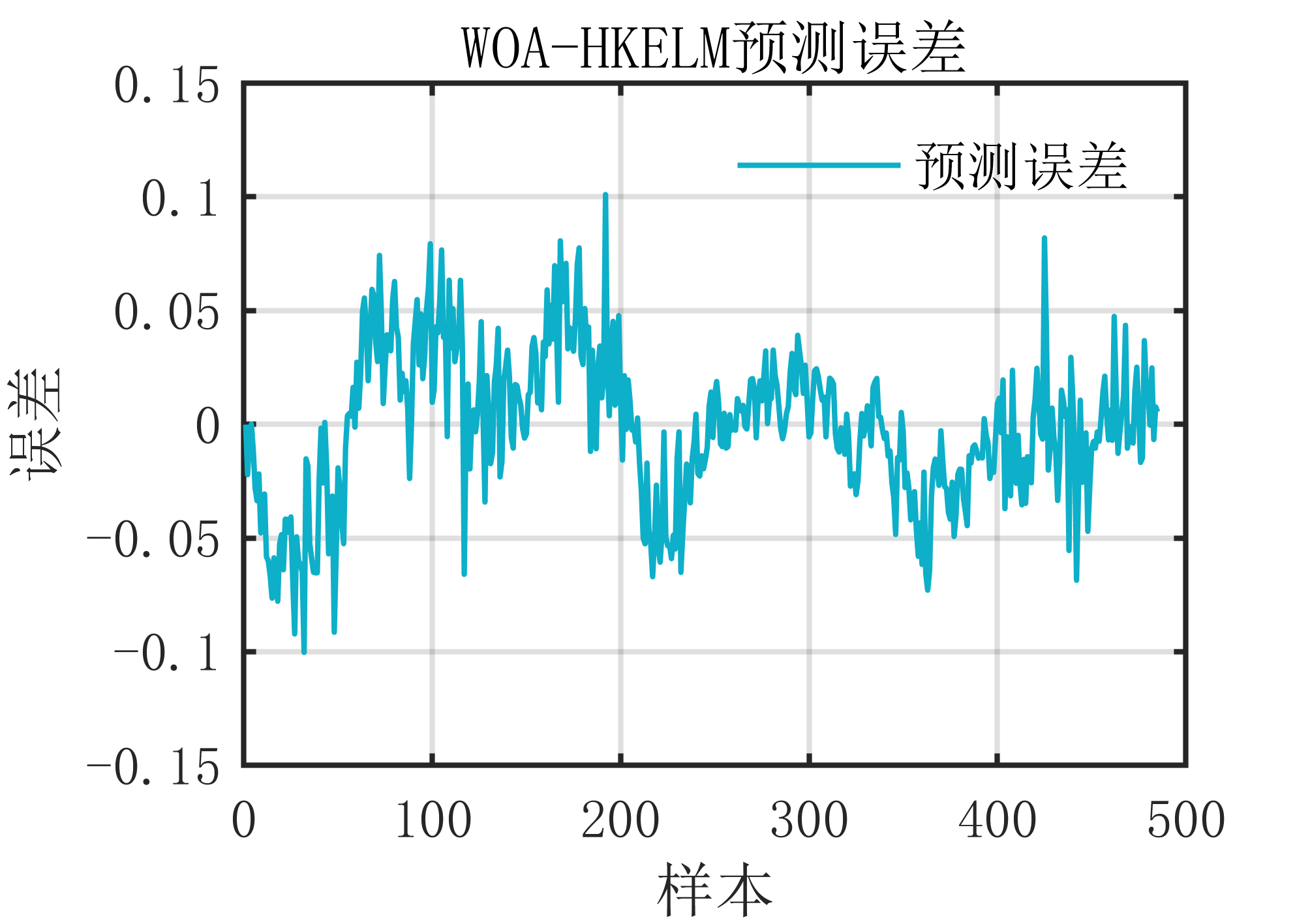
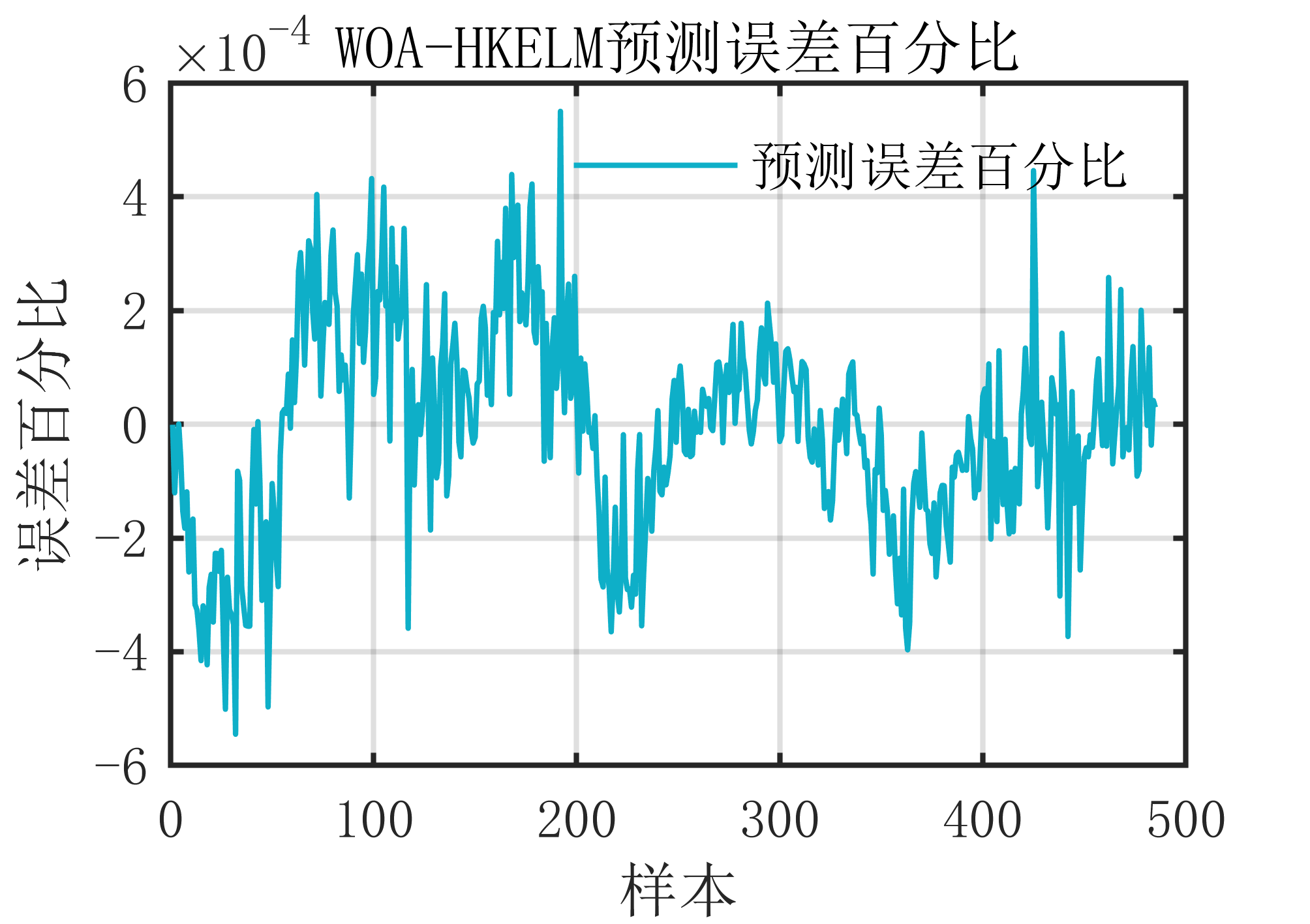
附视频教程操作:
【MATLAB】鲸鱼算法优化混合核极限学习机(WOA-HKELM)时序预测算法
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 基于Vue的应届毕业生财务管理系统-计算机毕业设计源码82886
- Oracle分区表
- 10、基于LunarLander登陆器的Dueling DDQN强化学习(含PYTHON工程)
- uniapp使用ucharts 自定义Y轴显示及刻度自定义
- 揭示AI未来趋势 | 张立赛博士带你畅游 GPT Store的技术革新之旅!
- Linux: dev: gcc: plugin: annobin
- 极智嘉(Geek+)货到人方案优势显著,助力拆零场景效率提升
- 打破无声世界:让您的网站会说话
- 基于YOLOv5+单目的物体距离和尺寸测量
- 南京航空航天大学-高等计算机网络复习