深度学习|交叉熵
什么是交叉熵
熵是用来衡量一个系统的混乱程度,混乱程度也其实代表着整个系统内部的不确定性。
信息量并不是指任意一种信息的量,它是指有助于减少系统内部不确定性的信息的量的大小。
也就是说信息量越大,系统混乱程度越小,熵也就越小。
而接下来的问题是怎么去衡量信息量的大小。
或者换种想法,这个衡量是用什么体系,用什么标准下去衡量(比如说人的生命在法律体系中是无价的,但在资本市场中,人的生命可以转化为劳动力商品,用工资进行结算)
如何构造信息量的函数

如果知道了阿根廷进了决赛且阿根廷赢了决赛,那么就可以知道阿根廷夺冠这件事情。其实也相当于说这两件事情是等价的。
如果将知道这件事情,看成是知道了这件事情背后的信息的话。
那么不妨假设有一个抽象函数f(某件事情)=对应的信息量。
于是有
f
(
A
B
)
=
f
(
A
)
+
f
(
B
)
f(AB)=f(A)+f(B)
f(AB)=f(A)+f(B)
而对数函数具有相同的性质
l
n
A
B
=
l
n
A
+
l
n
B
lnAB = lnA+lnB
lnAB=lnA+lnB
所以可以尝试用对数函数去拟合f函数。
所以不妨设
f
(
x
)
=
C
1
l
o
g
C
2
x
f(x)=C_1log_{C_2}x
f(x)=C1?logC2??x
关于 C 1 C_1 C1?参数的选择
f(x)中的x可以对应上x这种情况发生的概率,如果这个x越具体,信息量就越大,越多的限制条件,发生的概率将会越小。
也就是说f(x)要满足随着x的减小,反而有所增大。
所以C1为负数。
关于 C 2 C_2 C2?参数的选择
可以以e为底,也可以以2为底,其中以2为底的好处是,可以和计算机贴贴。(计算机底层是用二进制进行计算的,若采用2进制,和计算机会更加兼容)。
比如说一共有4位数据(16种可能),其中0101就可以唯一表示/确定出第5种可能。
(位数越多,说明情况越多,在从不确定的处境进入到确定的处境的过程越发艰难)
一个系统的熵
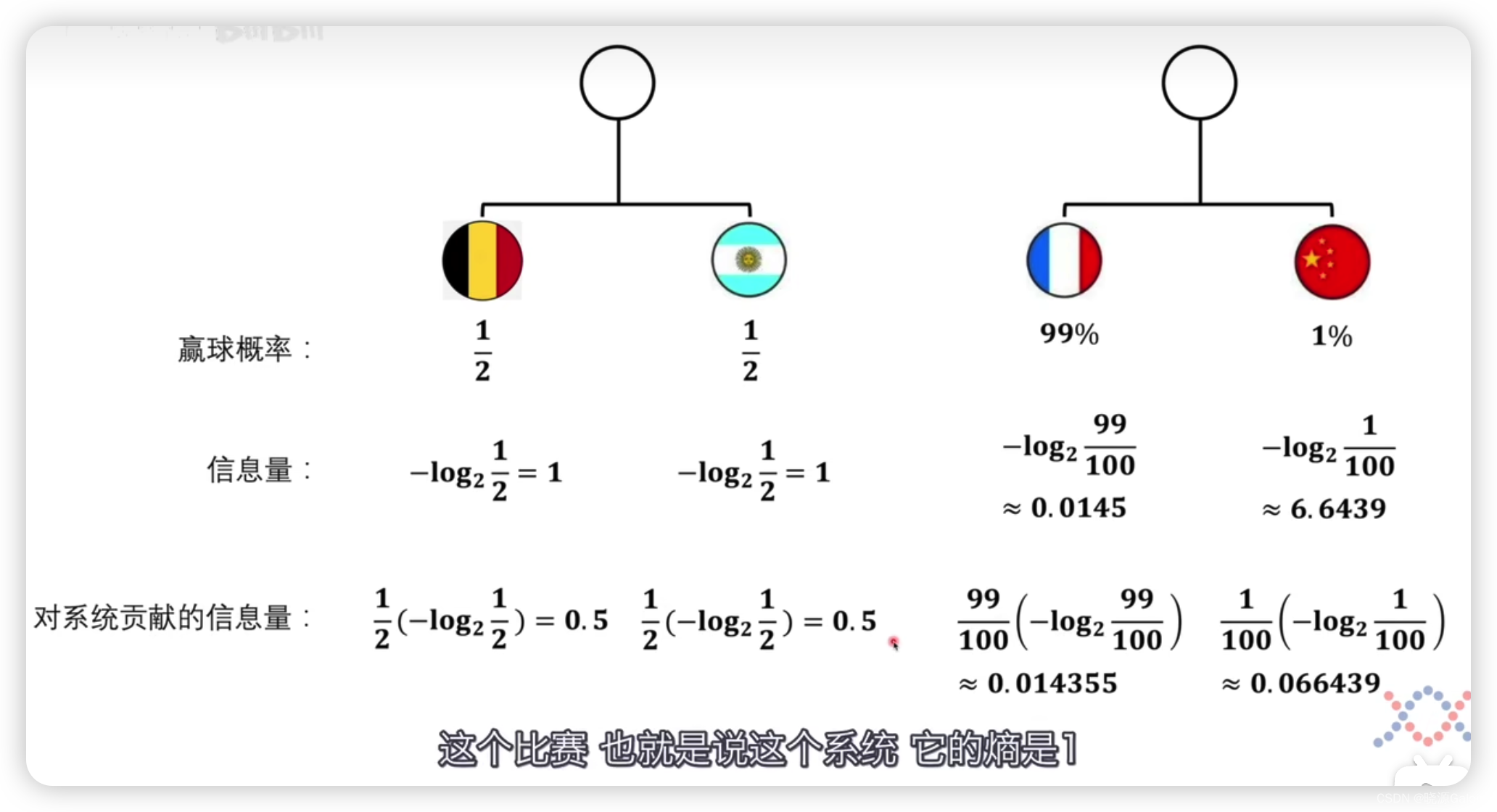
比如中国队和法国队打比赛,中国队要赢球的概率非常小,只有1%。也就是说赢起来艰难,赢的条件复杂,需要xx恰好跑位到xx位置,xx之前有认真训练,xx是真材实料的等等条件同时成立,也就是说为了达到1%的成功的确定,需要有很多的信息量。相对法国队赢球来说,中国队赢球的信息量会大很多。
但这是单看单个个体而言的。对于整个系统而言,要考虑单个个体的发生的概率,所以单个个体对整个系统的信息量的贡献为概率乘上对应的信息量。

如何比较两个系统的熵
最简单粗暴的想法是直接计算出两个系统的熵。但这是有问题的,不同模型/系统可能不同的评判标准,对同一件事情的信息量衡量出来的结果可能有所不同。
进而需要对这个熵,进行适当的修改——相对熵/KL散度
D
K
L
(
P
∣
∣
Q
)
D_{KL}(P||Q)
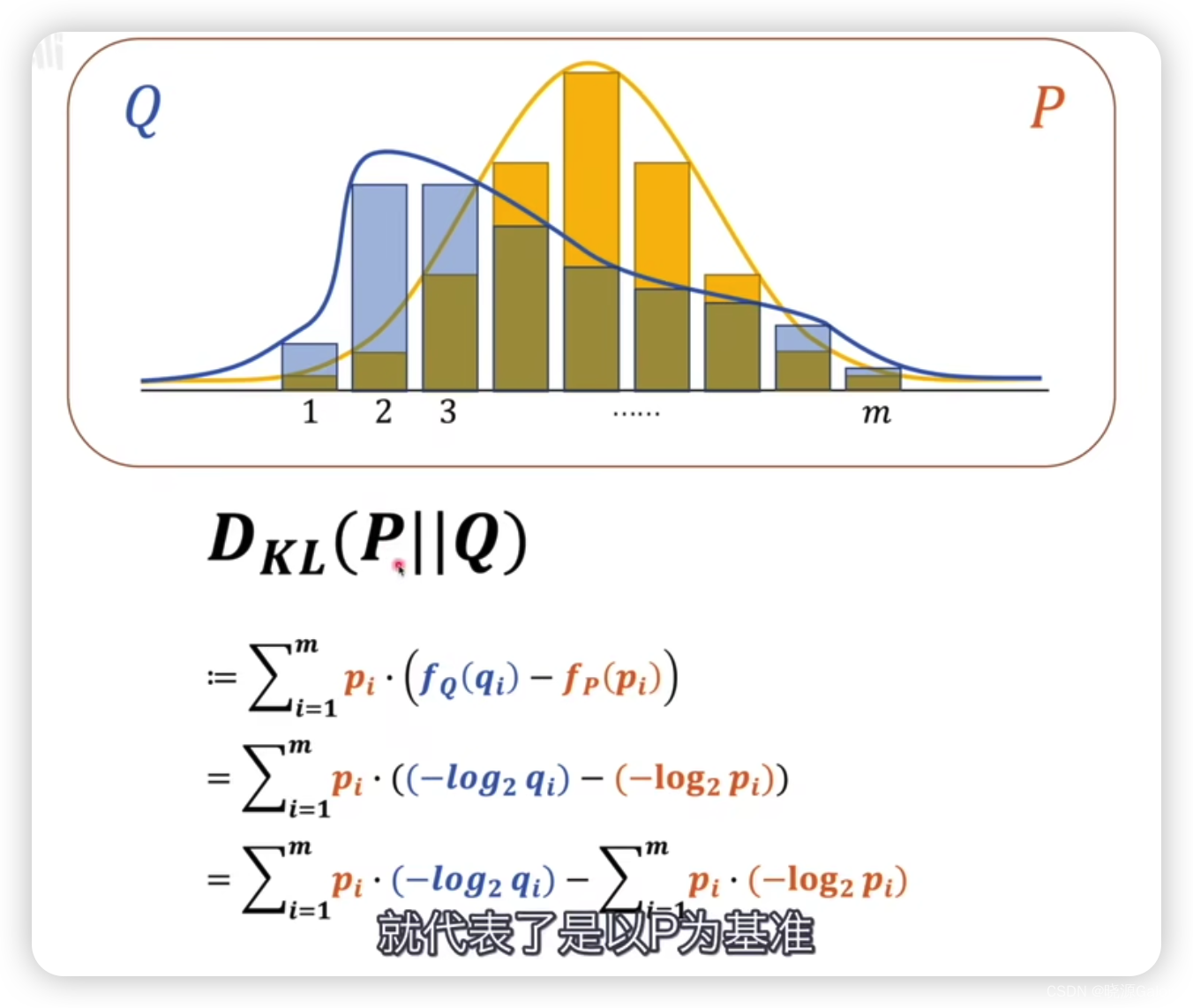
DKL?(P∣∣Q),其中P在Q的前面,代表以P作为基准,去衡量Q的差异。其中P和Q对应两套不同的概率模型。

按等式的直观感受
D
K
L
(
P
∣
∣
Q
)
D_{KL}(P||Q)
DKL?(P∣∣Q)相当于是将Q调整为P的各种情况下信息量之差的和。
由于f在前面已经有公式,所以可以进一步进行展开。


由于吉布斯不等式的存在,散度必然是大于0的。
交叉熵在神经网络中的应用
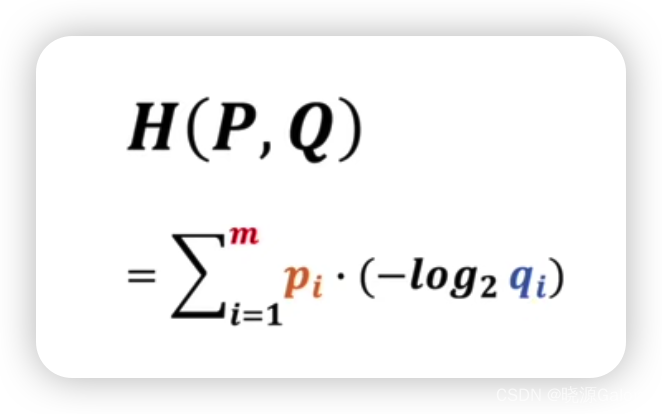
所以应用就是要找到其对应关系。
比如说
p
i
,
q
i
,
m
p_i,q_i,m
pi?,qi?,m分别对应神经网络中的什么?
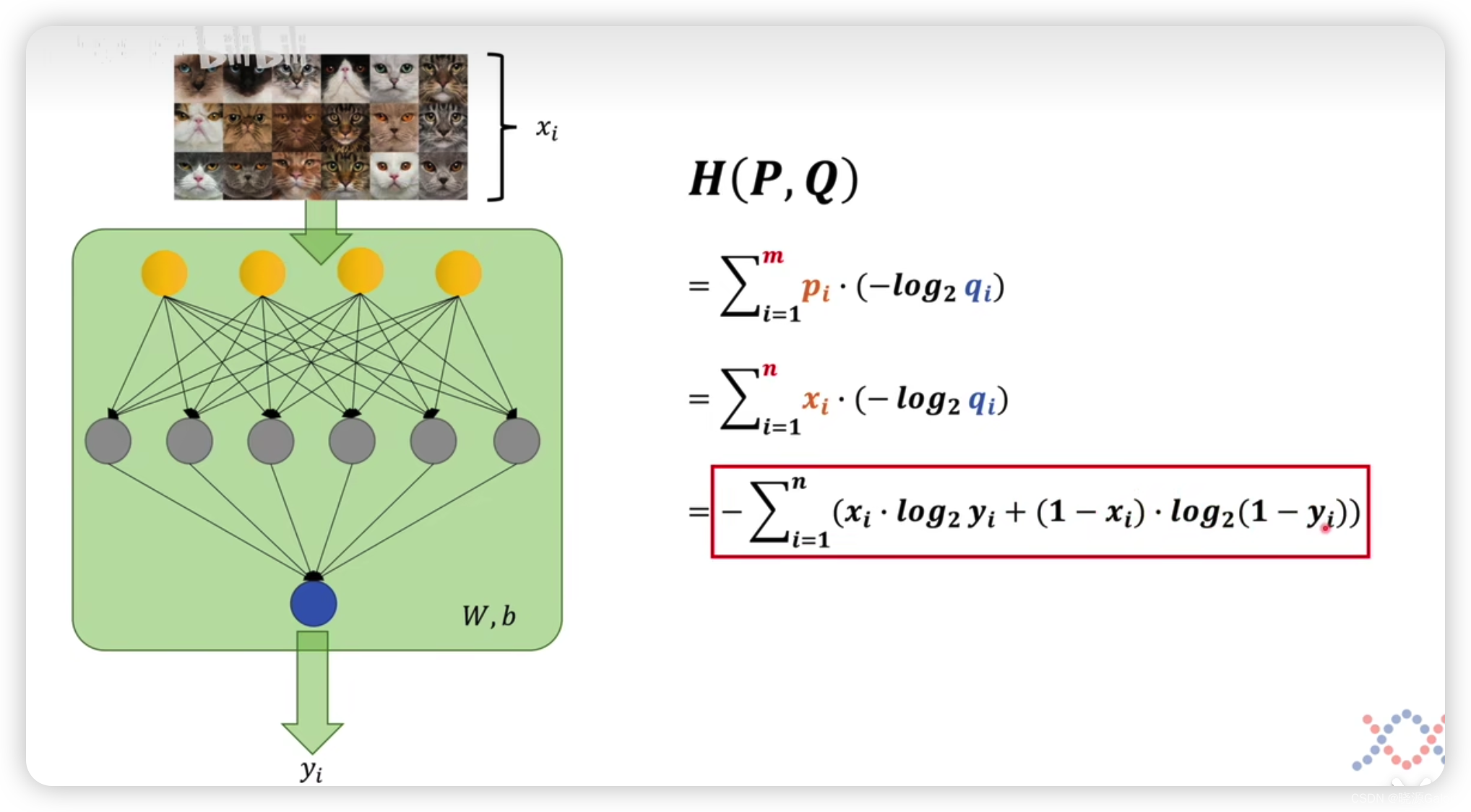
在神经网络中,可以用标签来代表
p
i
p_i
pi?(该情况出现的可能),用模型预测为猫的概率为
q
i
q_i
qi?,而m是要处理的图像的总量。

参考
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!