NOIP2010提高组T4:引水入城
题目链接
题目描述
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个 N N N 行 M M M 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
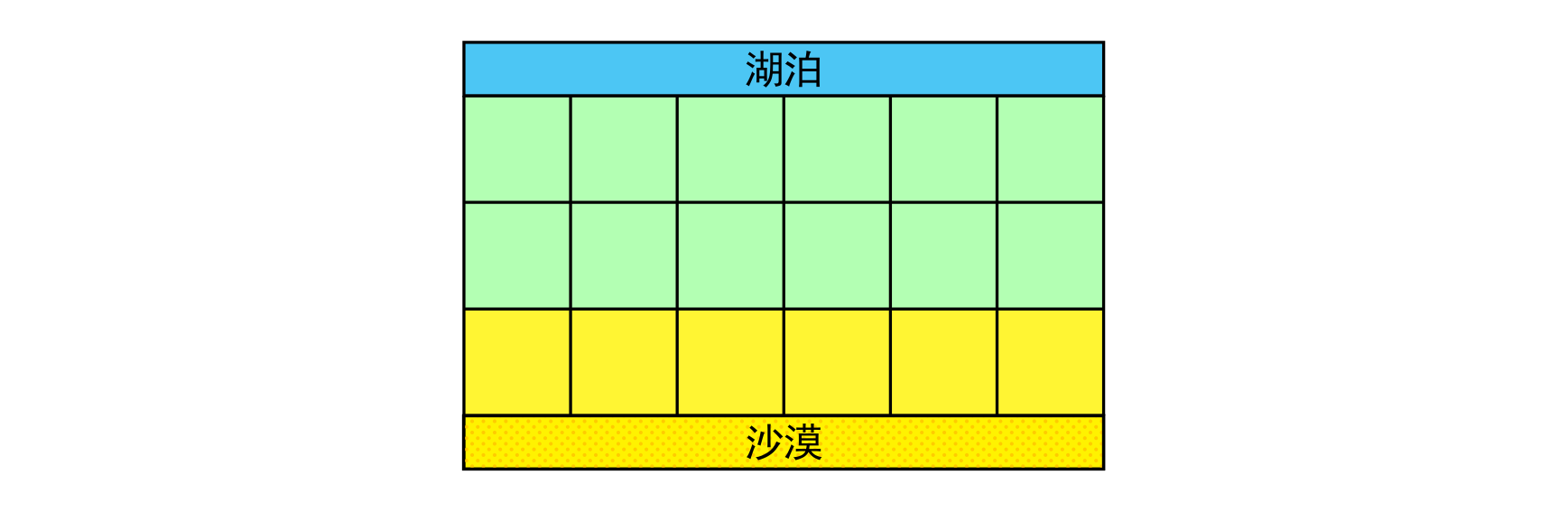
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第 1 1 1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第 N N N 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入格式
每行两个数,之间用一个空格隔开。输入的第一行是两个正整数 N , M N,M N,M,表示矩形的规模。接下来 N N N 行,每行 M M M 个正整数,依次代表每座城市的海拔高度。
输出格式
两行。如果能满足要求,输出的第一行是整数 1 1 1,第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数 0 0 0,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
样例 #1
样例输入 #1
2 5
9 1 5 4 3
8 7 6 1 2
样例输出 #1
1
1
样例 #2
样例输入 #2
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2
样例输出 #2
1
3
提示
样例 1 说明
只需要在海拔为 9 9 9 的那座城市中建造蓄水厂,即可满足要求。
样例 2 说明
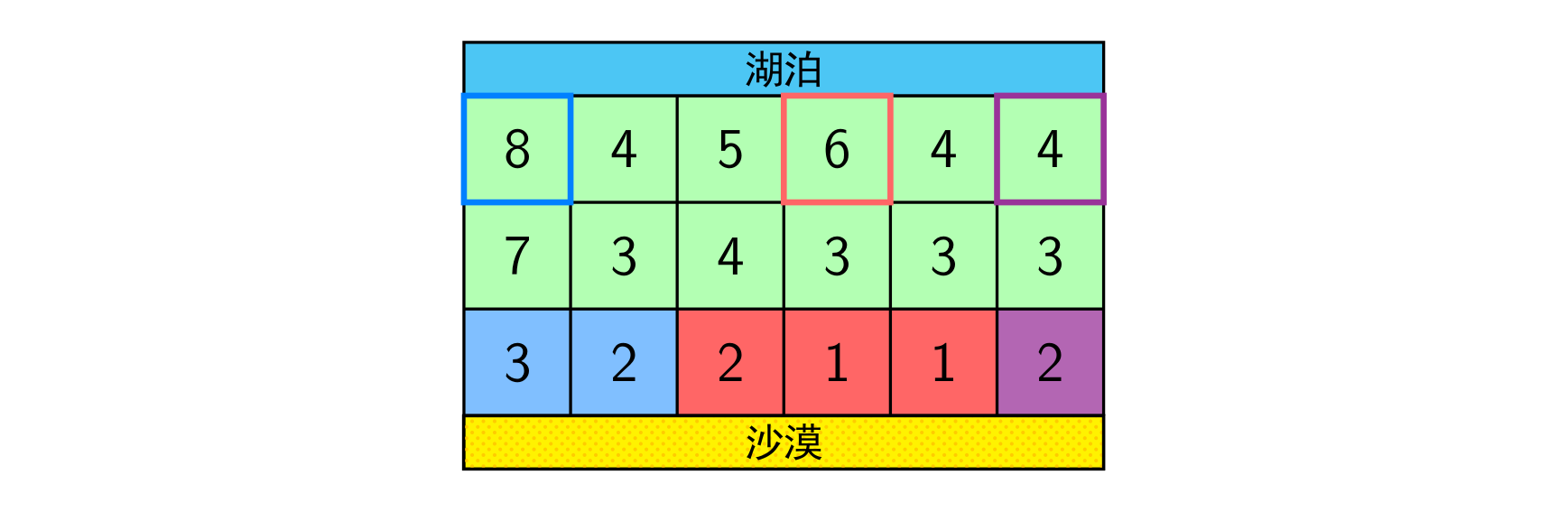
上图中,在 3 3 3 个粗线框出的城市中建造蓄水厂,可以满足要求。以这 3 3 3 个蓄水厂为源头在干旱区中建造的输水站分别用 3 3 3 种颜色标出。当然,建造方法可能不唯一。
数据范围
本题有 10 个测试数据,每个数据的范围如下表所示:
| 测试数据编号 | 能否满足要求 | N ≤ N\le N≤ | M ≤ M\le M≤ |
|---|---|---|---|
| 1 | 不能 | 10 10 10 | 10 10 10 |
| 2 | 不能 | 100 100 100 | 100 100 100 |
| 3 | 不能 | 500 500 500 | 500 500 500 |
| 4 | 能 | 1 1 1 | 10 10 10 |
| 5 | 能 | 10 10 10 | 10 10 10 |
| 6 | 能 | 100 100 100 | 20 20 20 |
| 7 | 能 | 100 100 100 | 50 50 50 |
| 8 | 能 | 100 100 100 | 100 100 100 |
| 9 | 能 | 200 200 200 | 200 200 200 |
| 10 | 能 | 500 500 500 | 500 500 500 |
对于所有 10 个数据,每座城市的海拔高度都不超过 1 0 6 10^6 106。
算法思想
分析测试样例可以发现,在第 1 1 1 行的城市建造蓄水厂,可以输送到第 N N N行一段连续的区间中,如下图所示:
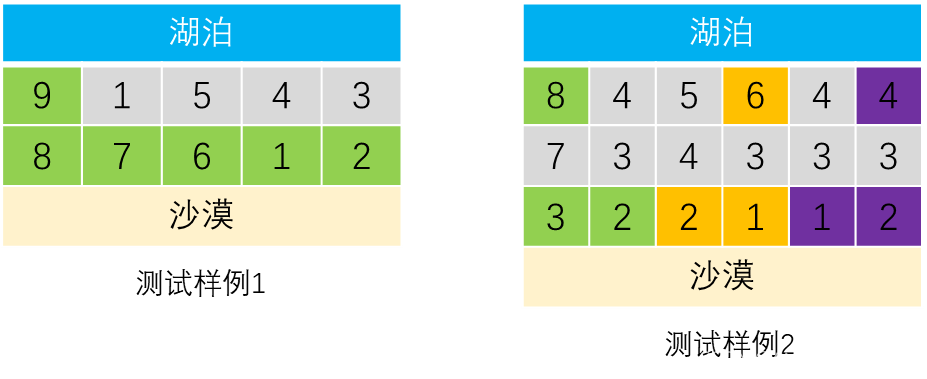
如果能求出第 1 1 1行每个格子能够“覆盖”的最大范围 [ L , R ] [L,R] [L,R],那么这个问题就变成用 M M M个闭区间,覆盖一个线段区间 [ 1 , m ] [1,m] [1,m]的区间覆盖问题。
例如:
- 测试样例1中, 8 8 8能够覆盖的范围是 [ 1 , 5 ] [1,5] [1,5],只用 1 1 1个区间就能完全覆盖。
- 测试样例2中,需要用 3 3 3个区间才能完全覆盖。
如何求每个格子能够“覆盖”的最大范围呢?由于每个格子只能向其相邻城市从高处向低处输送,那么其转移过程不可能有环,即存在拓扑序列,可以用动态规划的思想来解决。
状态表示
f [ x ] [ y ] f[x][y] f[x][y]表示第 x x x行第 y y y列的格子能够覆盖第 N N N行的最大区间 [ L , R ] [L, R] [L,R]
最终, f [ 1 ] [ i ] f[1][i] f[1][i]表示在第 1 1 1行第 i i i列建造蓄水厂能够在第 N N N行覆盖的最大区间。
状态计算
要在 1 1 1行的城市建造蓄水厂,就要枚举第 1 1 1行的每个格子,计算状态。由于是在方阵中进行状态转移,可以通过记忆化搜索的方式实现。
计算第 x x x行,第 y y y列的状态
- 枚举其相邻的 4 4 4个格子,不妨设为 [ a , b ] [a,b] [a,b];
- 如果能够从 [ x , y ] [x,y] [x,y]转移到 [ a , b ] [a,b] [a,b],那么递归计算 f [ a ] [ b ] f[a][b] f[a][b]
- f [ x ] [ y ] . L = m i n ( f [ x ] [ y ] . L , f [ a ] [ b ] . L ) f[x][y].L=min(f[x][y].L, f[a][b].L) f[x][y].L=min(f[x][y].L,f[a][b].L), f [ x ] [ y ] . R = m a x ( f [ x ] [ y ] . R , f [ a ] [ b ] . R ) f[x][y].R=max(f[x][y].R, f[a][b].R) f[x][y].R=max(f[x][y].R,f[a][b].R)
初始状态
- 由于使用记忆化搜索实现,将 f [ x ] [ y ] f[x][y] f[x][y]初始状态设为 [ ? 1 , ? 1 ] [-1,-1] [?1,?1]表示状态还没有计算过。
- 当计算到第 N N N行时, f [ x ] [ y ] f[x][y] f[x][y]的初始值应设为 [ y , y ] [y,y] [y,y],表示至少能够覆盖当前格子。
完成状态计算后,如果 f [ N ] [ i ] f[N][i] f[N][i]为 [ ? 1 , ? 1 ] [-1,-1] [?1,?1]表示第 N N N行第 i i i列无法被覆盖,即不可能建有水利设施。
时间复杂度
- 由于使用了记忆化搜索,每个格子只会搜索一次,因此时间复杂度为 O ( n × m ) O(n\times m) O(n×m)
- 区间覆盖问题的时间复杂度与区间数量 m m m相关,时间复杂度为 O ( m ) O(m) O(m)
代码实现
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 510;
typedef pair<int, int> PII;
PII f[N][N];
int n, m, h[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void dfs(int x, int y)
{
//状态已经计算过了
if(f[x][y].first != -1) return ;
f[x][y].first = N; //求最小值
if(x == n) f[x][y] = {y, y}; //计算到第n行时初始状态
for(int i = 0; i < 4; i ++) //枚举偏移数组
{
int a = x + dx[i], b = y + dy[i];
if(a < 1 || a > n || b < 1 || b > m) continue;
if(h[a][b] >= h[x][y]) continue;
dfs(a, b); //递归计算
f[x][y].first = min(f[x][y].first, f[a][b].first);
f[x][y].second = max(f[x][y].second, f[a][b].second);
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
cin >> h[i][j];
//初始状态
memset(f, -1, sizeof f);
//枚举第1行每一列进行状态计算
for(int i = 1; i <= m; i ++) dfs(1, i);
//计算不可能建有水利设施的城市数目
int res = 0;
for(int i = 1; i <= m; i ++)
if(f[n][i].first == -1) res ++;
if(res) printf("0\n%d", res);
else
{
//统计封闭区间
vector<PII> segs;
for(int i = 1; i <= m; i ++)
segs.push_back(f[1][i]);
//排序,求最小区间覆盖
sort(segs.begin(), segs.end());
int ans = 0, L = 1; //L表示要覆盖的区间左端点
for(int i = 0; i < m;)
{
int R = 0; //R表示能够覆盖L的区间的最大右端点
while(i < m && segs[i].first <= L)
R = max(R, segs[i ++].second);
ans ++;
if(R >= m) break; //完成覆盖
L = R + 1; //下次要覆盖的最左边位置
}
printf("1\n%d", ans);
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Jetson Orin Nano使用OpenCV获取视频帧率和帧数的方法
- ubuntu python播放MP3音频
- iOS - 真机调试的新经验
- redis 从0到1完整学习 (十七):内存回收之内存淘汰策略
- 圆心科技冲刺IPO:全链条医疗赋能,双增长动力强劲
- 【滑动窗口】C++算法:K 个不同整数的子数组
- 数据挖掘 模糊聚类
- 【Bootstrap学习】
- 恒驰喜讯 | 荣获华为云优秀服务伙伴奖!华为云生态大会2024开启联合解决方案新篇章
- 【计算机毕业设计】医院挂号系统小程序