模型之大脑和计算机的模型化

大脑和计算机的模型化

“素数分解：悬而未决的问题与计算机科学的挑战”

计算机同样也可以看作由相互作用的各部分集合而成；很大程度上由于这个原因，理论计算机科学中同样有很多悬而未决的重要问题。其中有如下这样一个例子，我们可能愿意去尝试解答。假设某人选取了两个素数p和q，将它们相乘后的结果pq告诉你。你只要逐个取素数，看看它是否能够整除pq，即可以找出p和q。例如，给出91，你很快就能发现它不是2,3，5的倍数，继而发现它恰好等于7X13。

“大整数因子分解：计算机科学的挑战与密码破解的可能性”

然而，当p和q非常大时——比方说都是200位的素数，那么这一试错过程会耗时极长，即使借助于强力计算机也是如此。（如果你想要体会一下这种困难，不妨尝试找出6901的两个素因子，以及280123的。）可另一方面，似乎也不难感觉到，说不定这个问题存在着更聪明的解决办法，基于它就可以编制出一种快速运转的计算机程序。如果能找到这种好办法，我们就能破解作为大部分现代安全系统之基石的密码，包括在互联网上以及其他各处——破解这些密码的难点就在大整数的因子分解。反之，如果能够表明由pq计算出p和q的这种快速有效的方法不存在的话，我们则能够安心。不幸的是，虽然计算机总在不断地让我们惊叹它的各种能力，对于它们做不了的，我们却几乎毫无了解。

“计算机数学模型：节点、门和边的简单规则”

在思考这个问题之前，我们必须找到一种方法来数学化地表示计算机，并且要尽可能简单。图4所显示的就是一种极好的方法。它包含许多层节点，连结点和点之间的线段称作“边”。进入最顶层的称作“输入”，这是一条0和1的序列，从最底层出来的叫作“输出”，是另一条0和1的序列。节点分为三种，分别称作“与门”、“或门”和“非门”。每一个门都从连结上层的边中接收到一些0和1。它再根据所接收到的数码来自己发出一些0和1，所遵循的简单规则如下；与门当接收到的输入全部为1时，输出1，否则输出0：或门当接收到的输入全部为0时，输出0，否则输出1；非门只允许一条边连结上层，它在接收到1时输出0，接收到0时输出1。

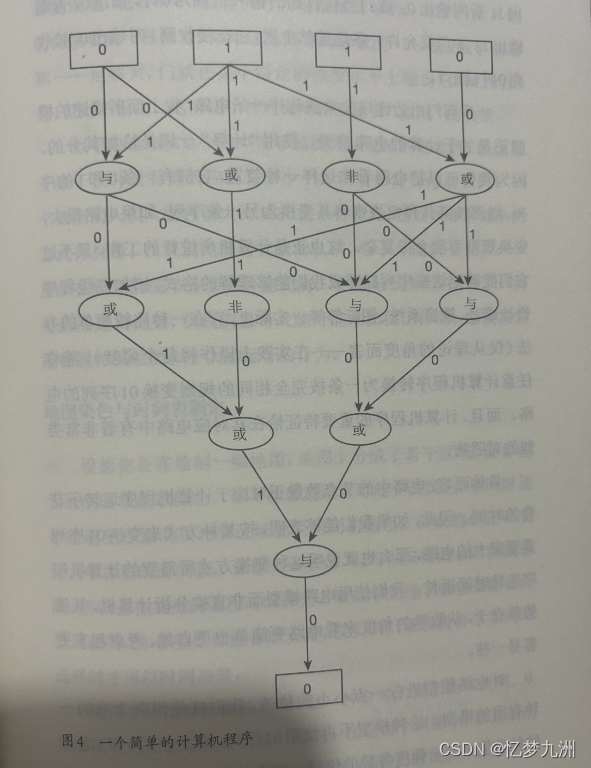
“计算机电路模型：序列变换与程序对应性的理论探讨”

一系列门由边连接起来就称作一条电路，我上面所描述的模型正是关于计算的电路模型。使用“计算”一词是恰如其分的，因为我们可以把电路看作这样一种装置，它拥有一条0和1的序列，继而按某些预定规则将其变换为另一条序列，如果电路很大，变换规则可能会很复杂。这也正是计算机所进行的工作，只不过它们能够把这些序列翻译成我们能够理解的格式，诸如高级程序设计语言、视窗系统、图标等等。实际上，存在一种比较简单的办法（仅从理论的角度而言——在实践上操作将是个噩梦），能将任意计算机程序转换为一条按完全相同的规则变换01序列的电路。而且，计算机程序的重要特征恰在其对应电路中有着非常类似的对照物。

“电路模型与计算机程序运行时间：简化分析与自然观察的优势”

具体而言，电路中的节点数量正对应于计算机程序运转所花费的时间。因此，如果我们能够表明，按某种方式来变换01序列需要庞大的电路，那么也就说明这种变换方式所需要的计算机程序运转时间很长。我们使用电路模型而非直接分析计算机，其优势就在于，从数学的角度来看电路更简单也更自然，考虑起来更容易一些。

“大脑模型：信号强度与神经元激发的简化表示”

对电路模型进行一点小小的修改，我们就能得到大脑的一种有用的模型。这种模型不再使用01序列，而是使用0和1之间的任意值来表示强度各异的信号。所有的门，即对应于神经元或者脑细胞，也有所不同，但其行为还是很简单的。每个门从其他的门接收到一些信号，如果这些信号的总强度——对应数字的总和——足够大，门就在某个特定的强度水平上输出它自己的信号，否则不输出。这对应于神经元所作的是否“激发”的决策。

“大脑模型的限制与应用：理论框架与行为模拟的可能性”

似乎很难相信这个模型能够捕捉大脑全部的复杂性，但这部分缘于我并没有提到应当有多少个门以及如何安排这些门。一个典型的人类大脑包含大约1000亿个神经元，它们以非常复杂的方式排列着；以我们当前对大脑的认识，还不可能谈及太多——至少在精微的细节方面不可能说清。不过，上述模型提供了一种有益的理论框架，供我们思考大脑可能是如何工作的，也使我们能够模拟某些类似于大脑运行的行为。

总结

通过电路模型和大脑模型，我们可以更好地理解计算机和大脑的运行方式。电路模型将计算机表示为由节点、门和边组成的电路，可以通过简单的规则进行序列变换，这种模型对于分析计算机程序运行时间有一定的优势。而大脑模型则使用信号强度来表示神经元的激发程度，每个门（神经元）根据接收到的信号决定是否输出信号。虽然这些模型无法完全捕捉计算机和大脑的复杂性，但它们提供了有益的理论框架，帮助我们思考它们的工作原理，并能够模拟一些类似的行为。尽管还有许多悬而未决的问题，如大整数因子分解和密码破解，但通过这些模型的研究，我们可以不断探索和理解计算机科学和神经科学的前沿。