diffusion入门

1. diffusion model 概念

https://zhuanlan.zhihu.com/p/638442430 这篇博客写得很好，顺便做一点笔记记录一下。
原博客附带的代码也很清晰易懂。

1.1 前向过程

后一个过程等于前一个结果的均值乘上sqrt(1-beta_t), 再加上方差beta_t的噪声。
这样下去可以得到 xt 基于 x0的公式， 也就是只要已知x0, 和每一步的beta_t可以求得任一阶段得 x_t
而且最终x_t接近 正态分布。

1.2 反向过程

1.2.1 之前我有一个问题:

---

正向x_t-1 到x_t 过程如下：
乘上一个数，再加噪声

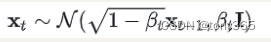
那么逆向从x_t 到 x_t-1这一步，是不是只需要减去 （x_t-1 到 x_t 添加的噪声） 再 （除以 sqrt(1-beta_t)其实等于sqrt(alpha_t)）， 是不是就可以了？ 当然是的。
x_t-1 = (x_t - beta_t * I) / sqrt(alpha_t)

但是公式推导的结果是下图这样的：
为什么呢？
因为这个里面的e_t 不是 x_t-1 到 x_t这个过程中添加的高斯噪声，而是从x_0 到 x_t 这个过程 对应的高斯噪声。 所以下面的是正确的。

所以是不是输入 x_t, t， 让网络预测I_t也是可行的？ 感觉也是可行的，只不过

1. forward 要一次求出所有阶段 x_1 ~ x_T, I_1 ~ I_T.
2. 输入 x_t, t， 让网络预测各个阶段的 I_t， 这里t = [1,T]
3. x_t-1 = (x_t - beta_t * I_t) / sqrt(alpha_t) 通过该过程逆向

1.2.2 回到原文

但是我们只知道 添加的噪声是符合正态分布的，不知道具体的数值，所以没办法逆向。
所以利用网络预测 e_t， 然后就可以通过公式求得的每一步的逆向过程来更新图像。
原博客写的更加清晰。

2. 一些改进的策略

参考https://zhuanlan.zhihu.com/p/586936791

1. 比如 beta的选择：改进后图像变化更均匀
   

2. 对生成步数的改进：
   原本模型训练的时候是假定在 T个时间步下训练的，在生成图像的时候，也必须从 T 开始遍历到 1 。而论文(https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/2102.09672.pdf)中提出了一种不需要重新训练就可以减少生成步数的方法，从而显著提升生成的速度。

   这个方法简单描述就是，原来是 T 个时间步现在设置一个更小的时间步数 S ，将 S 时间序列中的每一个时间步 s 和 T时间序列中的步数 t 对应起来

3. 相关介绍：

https://zhuanlan.zhihu.com/p/572161541
https://mp.weixin.qq.com/s?__biz=MzI1MjQ2OTQ3Ng==&mid=2247625397&idx=2&sn=e67b0e7ccf51aeedb4c0ab23310637b5&chksm=e9efe33ede986a28499a27014dcf7b44cbfe5841cf8d95b17f9ab46ab379cb2f237b204e1a9f&mpshare=1&scene=24&srcid=0124Qww3B4k9zexjSusblmGc&sharer_shareinfo=46fe1da3eadc5e0010ece1ac8ce51742&sharer_shareinfo_first=46fe1da3eadc5e0010ece1ac8ce51742&version=4.0.19.6020&platform=win#rd