用MATLAB求最短路径(graphshortestpath)和求最小生成树(minspantree),代码演示
发布时间:2024年01月05日
求最短路径(graphshortestpath),求最小生成树(minspantree)
1、最短路径问题
最短路径:从图中的某个顶点出发,到达另外一个顶点的所经过的边的权重之和最小的一条路径。
- 图:边和节点组成的结构,在数学建模中例如本题中道路和城市。
- 边:带有方向的是有向图,否则为无向图。
- 权重:每条边都有与之对应的值,本题中边道路,边的权重就是道路长度,当然是越小越好。
MATLAB求解最短路径:**Dijkstra算法,或MATLAB的graphshortestpath**函数
例: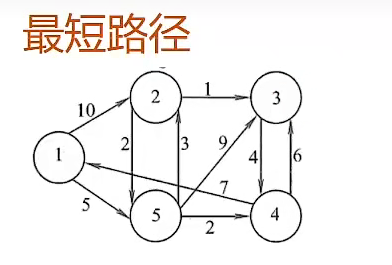
%sparse生成稀疏矩阵,也就是除了注明的几个元素外,其余都是0
%spare里第一个和第二个矩阵相同位置的元素值就是非零元素的索引
%非零元素的值
%w是每条边的权值
w=[10,5,2,1,4,6,7,3,9,2]
DG = sparse([1,1,2,2,3,4,4,5,5,5],[2,5,5,3,4,3,1,2,3,4],w)
% 没有就默认为零,这样快速生成一个稀疏矩阵
生成
% dist是最短路径的值, path是最短路径的节点顺序
% pred是到每一个节点的最短路径的终点前一个节点
% 如果求节点1到其他所有节点的最短路径呢?
[dist,path,pred] = graphshortestpath(DG,1,3) %后面的数字参数是起点和终点,然后计算最短路径
显示
% biograph生成图对象; view显示该图
point_name =["城市1", "城市2", "城市3","城市4", "城市5"]
h = view(biograph(DG,point_name, 'Showweights', 'on'))
优化
% 将最短路径的节点和边缘标记为红色并增加线宽
% getedgesbynodeid得到图h的指定边的句柄
% 第一个参数是图,第二个是边的出点,第三个是边的入点%句柄确保能找到对应的东西
% get查询图的属性,h.Nodes(path), 'ID'得到图h中最短路径的
% set函数设置图形属性
edges = getedgesbynodeid(h,get(h.Nodes(path),'ID')); %选取最短路径,并找到ID
set(edges,'LineColor', [1 0 0])% RGB数值,红绿蓝
set(edges,'Linewidth',2)
最终结果: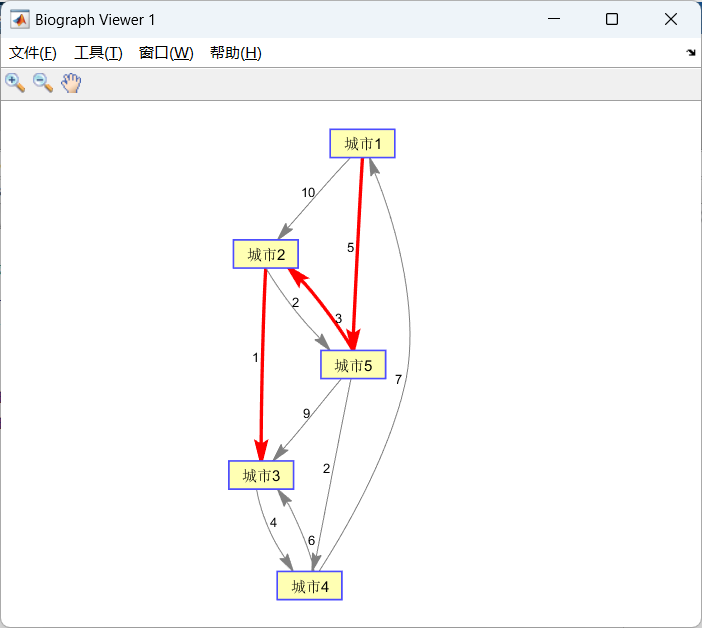
2、最小生成树
-
最短路径的区别:最短路径是针对某一顶点作为起点而言的,最小生成树是所有顶点连通且总路径最小。
-
最小生成树的求解:
MATLAB的
minspantree函数求解最小生成树,还有克鲁斯卡尔(Kruskal)算法,和普利姆(Prim)算法。
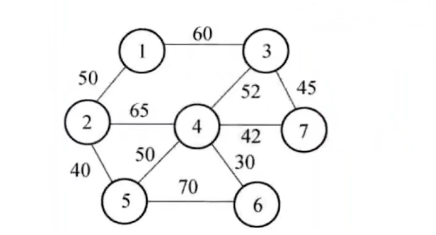
minspantree函数演示:
s = [1,1,2,2,3,3,4,4,4,5];
t = [2,3,4,5,4,7,5,6,7,6];
weights = [50,60,65,40,52,45,50,30,42,70];
%生成无向图,其中s和t对应元素代表着边,weights是权值
G= graph(s,t,weights);
%求出最小生成树,得到的T包含最小生成树的节点和对应边的权
T= minspantree(G);
% p = plot(G)就能把图片展现出来,后面是为了美观设置字体等
p = plot(G, 'EdgeLabel ',G.Edges.weight,"MarkerSize",8,'NodeFontSize',16,'EdgeFontSize',16)
%highlight突出显示绘制的图中的节点和边
highlight(p,T,'EdgeColor','red',"Linewidth",3)
在上述的代码中,T里面存的就是最小的生成树,而后续的操作只是为了更加的美观。
运行结果:
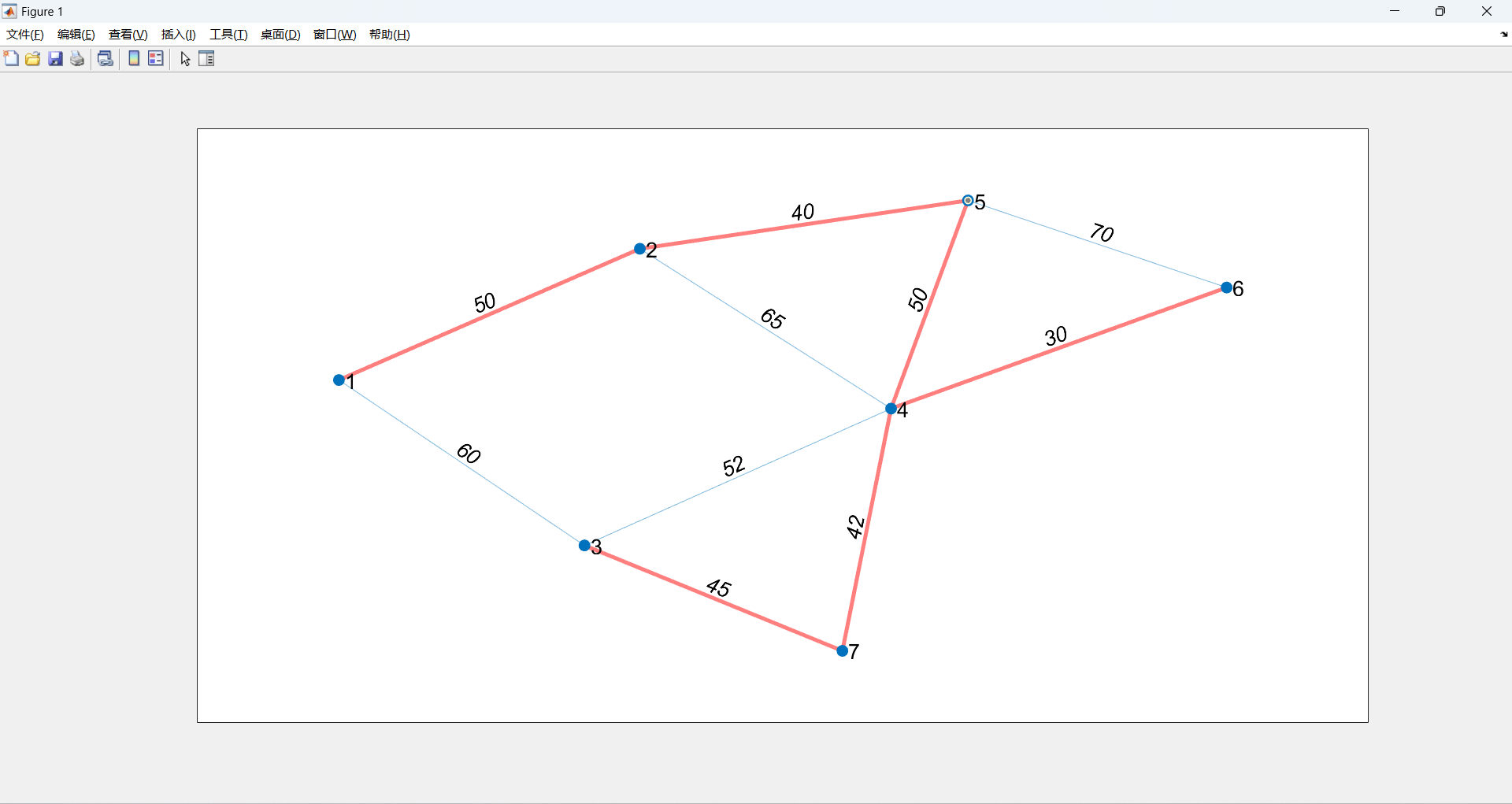
文章来源:https://blog.csdn.net/m0_63144319/article/details/135410102
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章